To drive safely and efficiently on the road, self-driving cars must have the ability to predict the behavior of participants in the surrounding traffic like a human driver. At present, the related research of trajectory prediction has received more and more attention. This article mainly solves one of the difficulties of trajectory prediction, that is, the multimodality of prediction. At the same time, another highlight of this article is the realization of predictions through convolutional raster images. The authors obtained the optimal prediction effect through experiments. This article has certain learning and reference value for research in the field of trajectory prediction.
Whether in terms of difficulty or potential social impact, autonomous driving is one of the biggest problems facing the field of artificial intelligence at present. Autonomous vehicles (SDVs) are expected to reduce road accidents and save millions of lives while improving the quality of life for more people. However, despite the considerable attention and industry players working in the field of autonomous driving, much remains to be done to develop a system that can operate at a level comparable to that of the best human drivers. One reason for this is the high uncertainty of traffic behavior and the large number of situations that SDVs can encounter on the road, making it difficult to create a fully generic system. To ensure safe and efficient operation, autonomous vehicles need to take this uncertainty into account and anticipate multiple possible behaviors of surrounding traffic participants. We solved this key problem and proposed a way to predict multiple possible trajectories while estimating their probabilities. The method encodes each participant's surroundings into a raster image as input to the deep convolutional network to automatically obtain relevant features of the task. After extensive offline evaluation and comparison with the latest benchmarks, the method successfully completed closed road tests on SDVs.
In recent years, unprecedented progress has been made in the field of artificial intelligence (AI) applications, and intelligent algorithms are quickly becoming an indispensable part of our daily lives. To cite a few examples that have affected millions of people: hospitals use AI methods to help diagnose diseases[1], matchmaking services use learned models to connect potential couples[2], and social media feeds are built through algorithms[3]. Still, the AI revolution is far from over and has the potential to accelerate further in the coming years. Interestingly, the automotive sector is one of the major industries, and the application of AI is still very limited so far. Large automakers have made some progress by using artificial intelligence (AI) in advanced driver assistance systems (ADAS)[5], however, its full capabilities remain to be harnessed through the emergence of new smart technologies, such as autonomous vehicles (SDVs).
Although driving a vehicle is a normal activity for many people, it is also a dangerous task, even for human drivers with several years of experience. While automakers are working to improve vehicle safety through better design and ADAS systems, year after year statistics show that much remains to be done to reverse negative trends on public roads. In particular, in 2015, the number of car accident deaths in the United States accounted for more than 5% of the total number of deaths,[7] and the vast majority of car accidents were caused by human factors[8]. Unfortunately, this isn't a problem that's only recently emerged, and researchers have been trying to understand why for decades. Research included investigating factors such as the effects of driver distraction[9], alcohol and drug use,[10],[11] and driver age[6], and how to most effectively get drivers to accept that they are fallible and most effectively influence their behavior.[12] Not surprisingly, a common theme in the existing literature is that humans are the most unreliable part of the transportation system. This can be improved through the development and widespread adoption of SDV. Recent breakthroughs in hardware and software technologies have made this prospect possible, opening the door to the field of robotics and artificial intelligence that could have had the biggest social impact to date.
Autonomous driving technology has been developed for a long time, and the earliest attempts can be traced back to the 1980s, research on AL-VINN [13]. However, it is only recently that technological advances have reached a point where they can be more widely used, such as the results of the 2007 DARPA Urban Challenge. Here, teams must navigate complex urban environments, deal with common situations on public roads, and interact with vehicles driven by humans and robots. These early successes have sparked tremendous interest in the field of autonomous driving, with many industry players (such as Uber and Waymo) and government agencies racing to build the technical and legal foundation for SDVs. However, despite progress, more work remains to be done to make SDVs operate at a human level and fully commercialized.
To operate safely and efficiently in the real world, a key challenge is to correctly predict the movements of the surrounding participants, and a successful system also needs to take into account their inherent multimodal properties. We focused on this task and built on the deep learning-based work we deployed[16], creating a bird's-eye view (BEV) raster that encodes high-definition maps and environments to predict the future of participants and make the following contributions:
(1) We extend the existing technique and propose a method that replaces the inference of a single trajectory and gives multiple trajectories and their probabilities;
(2) After extensive offline studies of the multi-hypothesis method, the method was successfully tested on SDV.
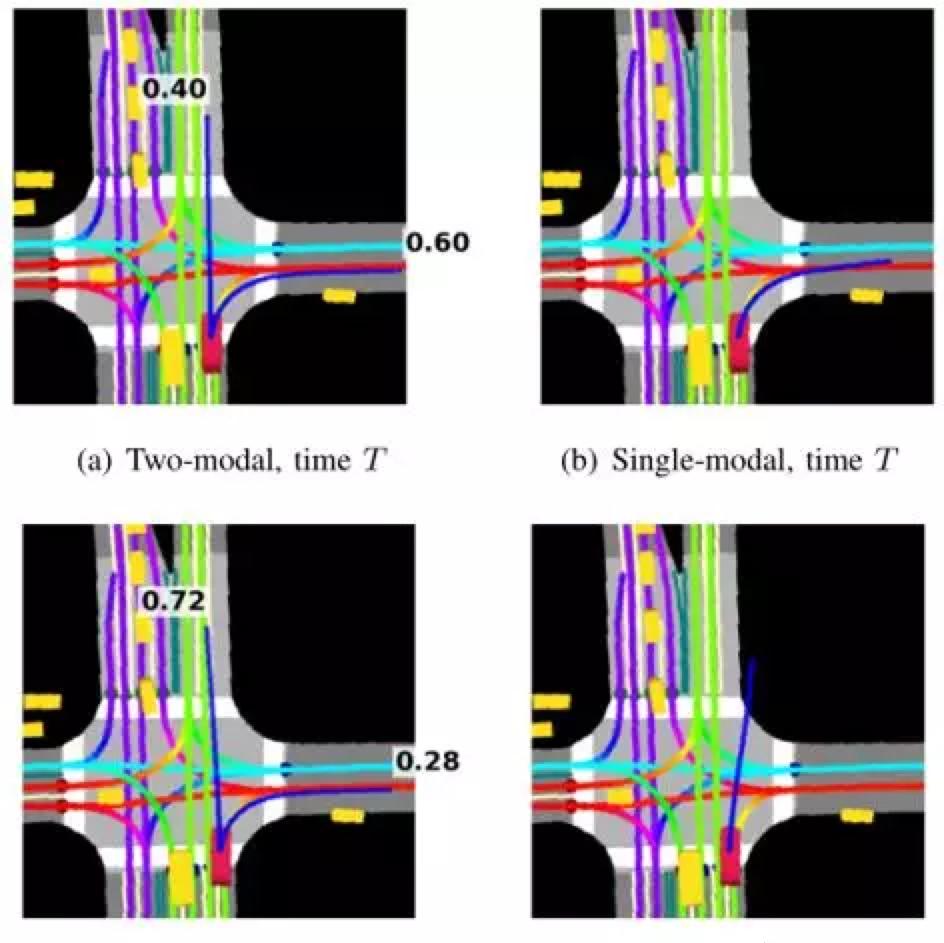
Figure 1 shows how our model captures the multimodality of the next 6-second trajectory. The method uses rasterized vehicle contexts, including high-definition maps and other participants, as model input to predict participants' movements in a dynamic environment. When the vehicle approaches the intersection, the multimodal model (where we set the modal number to 2) estimates that the probability of going straight is slightly lower than the probability of turning right, see Figure 1a. After three steps, the vehicle continues straight, at which point the probability of turning right drops significantly (Figure 1c); note that in fact the vehicle continues straight through the intersection. We can see that the single-mode model cannot capture the multimodality of the scene, but instead roughly predicts the average of the two modes, as shown in Figures 1b and 1d.
Related work
The issue of predicting the future actions of participants has been discussed in a number of recent publications. For a comprehensive overview of this topic, see [17] and [18], and in this section we will review the work from the perspective of autonomous driving. First, we will introduce engineering methods that are practically applied in the autonomous driving industry. We then discussed machine learning methods for motion prediction, with a particular emphasis on deep learning methods.
Motion prediction in autonomous driving systems
Most deployed autonomous driving systems use proven engineering methods to predict participants' movements. Common methods include calculating the future motion of an object by propagating the state of an object over time based on the assumptions of the underlying physical system and using techniques such as Kalman filtering (KF)[19],[20]. While this approach works well for short-term predictions, its performance degrades over a longer period of time because the model ignores its surrounding environment (e.g., roads, other participants, traffic rules). In response to this problem, Mercedes Benz[21] proposed a method that uses map information as a constraint to calculate the long-term future position of the vehicle. The system first associates each detected vehicle with one or more lanes on the map. All possible routes are then generated for each vehicle and associated lane pair based on map topology, lane connectivity, and vehicle current state estimates. This heuristic provides reasonable predictions in general, but it is sensitive to the error associated with the vehicle and lane. As an alternative to existing deployment engineering methods, the proposed method automatically learns from data that vehicles typically adhere to road and lane constraints, while at the same time well generalizing to various situations observed on the road. In addition, combining the existing idea of lane associations, we propose an extension of our approach.
Machine learning predictive models
The inability of artificially designed models to scale to many different traffic scenarios has prompted alternatives to machine learning models such as hidden Markov models,[22] Bayesian networks,[23] or Gaussian processes. Recently, researchers have focused on how to use inverse reinforcement learning (IRL) to simulate environmental context [25]. Kitani et al. [26] consider scenario semantics and use inverse optimal control to predict pedestrian paths, but existing IRL methods are inefficient for real-time applications.
The success of deep learning in many practical applications[27] has prompted research into its application in motion prediction. With the recent success of recurrent neural networks (RNNs), one of the research routes called long-short time memory (LSTM) has been used for sequence prediction tasks. The authors of the literature [28],[29] applied LSTM to predict the future trajectory of pedestrians in social interaction. In [30], LSTM is used to predict vehicle locations using past trajectory data. In [31], another RNN variant called a gated recursive unit (GRU) is combined with a conditional variational autoencoder (CVAE) for predicting vehicle trajectory. In addition,[32],[33] the motion of a simple physical system is predicted directly from image pixels by applying convolutional neural networks (CNNs) to a series of visual images. In [16], the authors propose a system in which CNNs are used to predict short-term vehicle trajectories and inputs are given BEV raster images encoding the surroundings of individual participants, which are subsequently also applied to vulnerable traffic participants.[34] Despite the success of these methods, they do not address the potential multimodality problem of the future possible trajectory required for accurate long-term traffic prediction.
There are currently many studies that solve the problem of multimodal modeling. Mixed density networks (MDNs)[35] are traditional neural networks that solve multimodal regression problems by learning the parameters of Gaussian mixture models. However, MDNs are often difficult to train due to numerical instability when operating in high-dimensional spaces.
To solve this problem, the researchers propose to train a network set [36], or train a network to produce M different outputs corresponding to M different hypotheses [37] using a loss that considers only the prediction result closest to the truth value. As a result of good experience, our work is built on these efforts. In addition, in [38], the authors introduce methods for multimodal trajectory prediction of road vehicles by learning a model that assigns probabilities to six maneuver categories. The approach requires a pre-defined set of possible discrete motivations, which can be difficult to define for complex urban driving. Alternatively, in [28], [29], [31], the authors suggest generating multimodal predictions by sampling, which requires repeated forward transfers to generate multiple trajectories. The proposed method directly calculates the prediction results of the multimodal state on a single forward CNN model.
Figure 2. The network framework presented in this article
Proposed method
In this section, we discuss the proposed multimodal trajectory prediction method for traffic participants, we first introduce the problem definition and the use of symbols, and then discuss the convolutional neural network structure and loss function we designed.
Problem definition
Suppose we can get sensors mounted on self-driving cars, such as lidar, ultrasonic radar, or real-time data streams from cameras. In addition, suppose this data is used in an existing detection and tracking system and outputs a state estimate S for all surrounding traffic participants (states including detection frame, position, velocity, acceleration, heading, and rate of change in heading angle). Defines a set of discrete times for the evaluation of the output state of the tracker, with a fixed time interval between successive time steps (0.1s when the tracker is operating at 10Hz). Then, we define the state output of the tracker at the tj moment to the ith traffic participant as sij, where i=1,..., Nj. Nj is the number of all traffic participants that are tracked at the tj time. Note that in general, the number of traffic participants is constantly changing because new traffic participants will appear within the sensor's perceptual range and the traffic participants that were originally tracked will be outside the sensor's perceptual range. Moreover, we assume that detailed high-precision map information on the driving area of the self-driving car can be obtained, including road and sidewalk locations, lane directions, and other related map information.
Multimodal trajectory modeling
Based on our previous work [16], we first rasterized a BEV raster image that encodes the traffic participant's map environment and the surrounding traffic participants (such as other vehicles and pedestrians, etc.), as shown in Figure 1. Then, given a raster graph and state estimation sij of the ith traffic participant at the tj moment, we use a convolutional neural network model to predict M possible future state sequences, as well as the probabilities of each sequence. where m represents the modal number and H represents the predicted time step. For a detailed description of the rasterization method, the reader is invited to consult our previous work [16]. Without losing the generality, we simplify the work, we only infer the future x and y coordinates of the ith traffic participant instead of the full state estimate, while the rest of the state estimate can be obtained by the state sequence and the future position estimate. At the tj moment, the past and future position coordinates of the traffic participant are relative to the position of the traffic participant at the tj moment, where the forward direction is the x-axis, the left-hand direction is the y-axis, and the center of the traffic participant detection frame is the origin.
The network structure proposed in this article is shown in Figure 2. The input is an RGB raster graph with a resolution of 0.2 meters at 300*300 and the current state of the traffic participants (speed, acceleration, and rate of change in the angle of direction), and the output is the future x-coordinate and y-coordinate of M modes (each mode has 2H outputs) and their probabilities (one scalar per mode). So each traffic participant has an output of (2H+1)M. The probability output is then passed to the softmax layer to guarantee that their sum is 1. Note that any convolutional neural network structure can be used as a base network, where we use MobileNet-v2.
Multimodal optimization function
In this section we discuss the loss function of the multimodality inherent in our proposed modeling trajectory prediction problem. First, we define the single-modal loss function of the mth mode of the ith traffic participant at tj time as the average displacement error (or L2 norm) between the truth trajectory point and the predicted mth mode.
A simple multimodal loss function we can use directly is the ME loss, defined as follows:
However, as can be seen from our assessment in section IV, ME losses are not suitable for trajectory prediction problems due to modal collapse problems. To solve this problem, we were inspired by [37] to propose the use of a new multi-trajectory prediction (MTP) loss that explicitly simulates the multimodality of the trajectory space. In the MTP method, for the ith traffic participant at the tj moment, we first obtain the M-bar output trajectory through the forward propagation of the neural network. We then use an arbitrary trajectory distance formula to determine the modal m closest to the truth trajectory.
After selecting the best matching mode m, the final loss function can be defined as follows:
Here I is a binary indicator function, if the condition c is true it is equal to 1, otherwise it is 0, is a classified cross-entropy loss, defined as:
α is a hyperparameter used to weigh two losses. In other words, we make the probability of the most matching mode m close to 1 and the probability of other modes close to 0. Note that during training, the output of the position updates only the optimal mode, while the output of probability updates all modes. This allows each pattern to be specifically targeted for different categories of participant behavior (e.g., straight walking or turning), which successfully solves the problem of modal collapse, as shown in the next experiment.
Figure 3: Modal selection method (modalities are represented in blue): When using displacement, the truth value (green) matches the right turn mode, while when using the angle, it matches the straight mode
We experimented with several different trajectory distance functions. Especially as the first option, we use the average displacement between the two trajectories. However, this distance function does not model the multimodal behavior at the intersection very well, as shown in Figure 3. To solve this problem, we propose a ranging function that improves the handling of intersection scenes by considering the angle between the current position of the traffic participant and the truth value and the last position of the predicted trajectory. Section 4 gives quantitative comparison results.
Finally, for losses (2) and (4) we train convolutional neural network parameters to minimize losses on the training set.
Note that our multimodal loss function is an unknowable choice of one of the modes as the loss function, and it is easy to generalize our method to the paper [16] proposed in the paper [16] using negative Gaussian log likelihood to predict the uncertainty of the trajectory points.
Lane lines follow multimodal predictions
Earlier we described a method that can predict multiple modes directly in a forward propagation process. In [21], where each vehicle is associated with a lane (i.e., a lane line follows the vehicle), we propose a method to implicitly output multiple trajectories. In particular, assuming that we know the lane lines that are likely to be followed and the lane lines that are impossible to follow are filtered out by the lane line scoring system, we add another raster layer to encode this information and train the network to output the lane line follow trajectory. Then, for a scene, we can effectively predict multimodal trajectories by generating raster plots followed by multiple different lane lines. To generate a training set, we first determine the lane lines that the vehicle actually follows and build an input raster map based on this. We then train the lane line following (LF) model using the loss function described earlier by setting M=1 (ME and MTP are equal in this case). In fact, LF and other methods can be used simultaneously, dealing with lane line following and other traffic participants, respectively. Note that we are introducing this approach for completeness only, as practitioners may find it helpful to combine the idea of rasterization with existing lane line following methods to obtain multimodal predictions, as described in [21].
Figure 4. Example of trajectory output of an LF model that follows lane lines differently in the same scene (pale pink representation)
In Figure 4 we show a raster plot of the same scene, but using two different trailing lane lines marked with pale pink. One is straight and the other is left. The trajectory output by this method follows a predetermined path well and can be used to generate multiple predicted trajectories for vehicles following lane lines.
experiment
We collected 240 hours of data by manually driving in pittsburgh, PA, Phoenix, AZ, and other different traffic conditions (e.g., different time periods, different days). Raw sensor data is taken from cameras, lidar, and ultrasonic radar, using UKF[40] and kinematic models[41] to track j traffic participants, and output status estimation for each tracking vehicle at a rate of 10Hz. The UKF is highly optimized and trained on large amounts of labeled data and extensively tested on large-scale real data. Each traffic participant's tracking moment at each discrete moment is equivalent to a single data point1, and after the static traffic participant is deleted, the overall data has 7.8 million data points. We considered a prediction time of 6 seconds (i.e. H=60), α=1, and obtained the training, validation, and testing sets using a 3:1:1 split ratio.
We compare the proposed approach with several baselines:
(1) Real-time estimation of the status of the forward UKF
(2) Single trajectory prediction (STP)[16]
(3) Gaussian mixed trajectory space MDN[35]
The model was implemented on TensorFlow[42] and trained on a 16Nvidia Titan X GPU card. We trained using the open source distributed framework Horovod[43] and completed it in 24 hours. We set the number of batches processed per gpu to 64 and trained using Adam optimizer[44], setting the initial learning rate to 10-4, reducing it by a factor of 0.9 every 20,000 iterations. All models are trained end-to-end and deployed to self-driving cars, using GPUs to perform batch processing, with an average time of about 10ms.
Experimental results
We compare methods using error measures associated with motion prediction: displacement (1), and errors along and cross tracking [45] measure longitudinal and lateral deviations from truth values, respectively. Since the multi-grinding method provides probabilities, one possible evaluation method is to use the prediction error of the most likely mode. However, earlier studies of multimodal predictions[31] found that such metrics favored single-mode models because they apparently optimized for average prediction errors while outputting untrue trajectories (see example in Figure 1). We mirror the existing settings from [31] and [37], filter out the low probability trajectories (we set the threshold to 0.2), and use the minimum error mode of the remaining settings to calculate the metric. We found that the results calculated in this way are more in line with the observational performance on self-driving cars.
Table 1. Comparison of prediction errors of different methods (in meters)
In Table 1 we give the error of predicting steps of 1s and 6s, an average metric of the first level of different numbers of modal M over the entire predicted step (modal number from 2 to 4). First we can see that single-mode models such as UKF and STP are clearly not suitable for up-time prediction. However, their short-term prediction results at 1s are reasonable, and the prediction error of 6s is significantly greater than that of the optimal multimodal method. Such results are to be expected, as in the short term traffic participants are limited by physics and their surroundings, resulting in an approximate single-mode distribution of truth values [16]. On the other hand, the multimodality of the prediction problem becomes more pronounced from a long-term perspective (e.g., when a traffic participant approaches an intersection, they may make several different choices in the exact same scenario). Single-mode prediction does not take this problem into account very well, but directly predicts the average of a distribution, as shown in Figure 1.
In addition, it is worth noting that for various M values, MDN and ME give results similar to those given by STP. The cause is the well-known modal collapse problem, in which only one modal provides a non-degenerative prediction. Thus, in practice, an affected multimodal approach would fall back into a single mode and would not be able to fully capture multiple modes. [37] The authors reported this problem with MDNs and found that the multimodal hypothesis model was less affected, which was further confirmed by our experimental results.
Shifting our focus to the MTP method, we observed a significant improvement over other methods. Both the average error and the error at the 6s hour decreased across the board, suggesting that these methods learned the multimodality of traffic problems. The prediction error of short-term 1s and long-term 6s is lower than that of other methods, even if the effect of long-term prediction is more obvious. Interestingly, the results show that when M = 3, all evaluation indicators are optimal.
Table 2. Displacement error at 6s for different modes
Next, we evaluated different trajectory distance metrics to select the best matching mode in MP training. Table 1 shows that using displacement as a distance function is slightly better than using angles. However, to better understand the implications of this choice, we divided the test set into three categories: left turn, right turn, and straight (95% of the traffic participants in the test set were roughly straight, and the rest were evenly distributed between turns), and the results of the 6s prediction were reported in Table 2. We can see that the use of angles improves the handling of turns, as well as very slight degradation of straight conditions. This confirms our hypothesis that angle matching strategies improve performance at intersections, which are critical to the safety of self-driving cars. With these results in mind, in the remainder of this section, we will use the MTP model of the angular modal matching strategy.
Figure 5. From left to right, correspond to the influence of 1 to 4 different modes on the output trajectory
In Figure 5, when increasing the number of modal M, we can see that when M = 1 (i.e. the inferred trajectory is roughly the average of the straight-line mode and the right-turn mode). Increasing the number of modes to 2, we get a clear separation of straight and right turn modes. In addition, setting M to 3 creates a left-turn mode, although the probability is low. When we set it to M=4, we found an interesting result, the straight-line mode is divided into "fast" and "slow" modes, modeling the longitudinal speed of the traffic participant. We noticed the same effect on straights away from intersections, where the straight mode splits into several different speed modes.
Figure 6. Analysis of modal probability correction
Finally, we analyzed the calibration of the predicted modal probabilities. In particular, using the test set, we calculated the relationship between the predicted modal probability and the modal probability that best matched the truth trajectory. We segmented the trajectory based on its predicted probability and calculated the average modal match probability for each segment. Figure 6 shows the result we use M=3, and the result of M for other values is similar to the one shown. We can see that the redraw is very close to the y=x reference line, indicating that the predicted probabilities are well calibrated.
Due to the uncertainty inherent in the behavior of traffic participants, in order to ensure safe and efficient driving on the road, self-driving cars need to consider multiple possible future trajectories of the surrounding traffic participants. In this paper, we address this key aspect of the autonomous driving problem and propose a multimodal modeling method for vehicle motion prediction. The method first generates a raster map encoding the surroundings of the traffic participants and outputs several possible predicted trajectories and their probabilities using a convolutional neural network model. We discussed several multimodal models and compared them with the most advanced methods available today, and the results show that the method proposed in this paper has practical benefits. After extensive offline evaluation, the method was successfully tested on self-driving cars.
bibliography
[1] F.Amato,A.López,E.M.Pe a-Méndez,P. Vaňhara, A.Hampl,and J.Havel,"Artificial neural networks in medical diagnosis,"Jounal of Applied Biomedicine,vol.11,no.2pp.47-582013.
[2] K.Albury,J.Burgess,B.Light,K.Race,and R.Wilken,"Data cultures of mobile dating and hook-up apps: Emerging issues for critical social science research,"Big Data & Society,vol.4,no.2,2017.
[3] I.Katakis,G.Tsoumakas,E.Banos,N. Bassiliades, and I. Vlahavas. An adaptive personalized news dissemination system,Journal of Intelligent Information Systems,vol.32,no.2,pp.191-212,2009[4]Y.N.Harari,"Reboot for the ai revolution," Nature News, vol.550 no.7676,p.324,2017.
[5] A.Lindgren and F.Chen,"State of the art analysis: An overview of advanced driver assistance systems (adas) and possible human factors issues,"Human factors and economics aspects on safety,pp.38-502006.
[8] S.Singh, "Critical reasons for crashes investigated in the national motor vehicle crash causation survey,National Highway Traffic Safety Administration,Tech.Rep.DOT HS 812 115,February 2015.
[9] F.A.Wilson and J.P. Stimpson,“Trends in fatalities from distracted driving in the united states,1999to 2008,American journal of public health,vol.100no11,pp2213-2219,2010.
[12] R. Na t nen and H. Summala,"Road-user behaviour and traffic accidents,Publication of: North-Holland Publishing Company,1976
[13] DA. Pomerleau,Alvinn:An autonomous land vehicle in a neural network,"in Advances in neural information processing systems,1989 pp305-313.
[14] M.Montemerlo,J. BeckerSBhatH.Dahlkamp,D.Dolgov S.EttingerD.HaehnelTHildenGHoffmannB.Huhnke,et al. Junior: The stanford entry in the urban challenge,"Journal offield Robotics,vol25,no9,pp569-597,2008.
15]CUrmson et al." Self-driving cars and the urban challenge"IEEE Intelligent Systemsvol23no.22008.
[16] N.Djuric,V.RadosavljevicH.CuiTNguyen,F.-C.Chou,T-H. Lin and J.Schneider“Short-term motion prediction of traffic actors for autonomous driving using deep convolutional networks,"arXiv preprint arXiv:1808058192018
[18] J.Wiest, Statistical long-term motion prediction. Universit t Ulm 2017.
[19] R.E.KalmanA new approach to linear filtering and prediction problems,"Transactions ofthe ASME-Journal ofBasic Engineering vol.82no.Series Dpp35-451960.
20]ACosgunL.Ma,et al,"Towards full automated drive in urban environments:Ademonstrationin gomentum station,california,"in IEEE Intelligent Vehicles Symposium,2017,pp1811-1818 [Online]Available:https://doiorg/101109/1VS20177995969
[21] J.Ziegler,P.BenderM.Schreiber,et al,“Making bertha drive-an au-tonomous journey on a historic route,"IEEE Intelligent Transportation Systems Magazine,vol6pp8-20102015.
[22] TStreubel and KH. Hoffmann, Prediction of driver intended path at intersections. IEEE,Jun 2014. [Online]. Available http://dxdoiorg/10.1109/VS.2014.6856508
[23] M.Schreier, V. Willert, and J.Adamy,“An integrated approach to maneuver-based trajectory prediction and criticality assessment in arbitrary road environments,"IEEE Transactions on Intelligen Transportation Systems,vol17no10p2751-2766Oct 2016[Online]. Available:http://dxdoiorg/10.1109/TITS.2016.2522507
[24] J.Wang,D.Fleet,and A.Hertzmann,“Gaussian process dynamical models for human motion,"IEEE Transactions on Pattern Analysis and Machine Intelligence,vol.30,no.2p.283-298Feb2008 [Onlinel.Available:http://dxdoi.org/10.1109/TPAMI.2007.1167
[25]A.Y.Ng and S.Russell,"Algorithms for inverse reinforcement learning, in International Conference on Machine Learning,2000
[26] K.M.Kitani,B.D.Ziebart,J. A.Bagnell, and M.Hebert, Activity Forecasting. Springer Berlin Heidelberg,2012p.201-214. [Online] Available:http://dxdoiorg/10.1007/978-3-642-33765-9_15
[28] A.Alahi,K. Goel, et al. Social LSTM:Human Trajectory Prediction in Crowded Spaces. IEEE,Jun 2016.Online]. Availables http://dxdoi.org/10.1109/CVPR.2016.110
[29] A.Gupta,J.Johnson,L.Fei-Fei,S.Savarese,and A.Alahi“Social gan: Sociallyacceptable trajectories with generative adversarial networks, in The IEEE Conference on Computer Vision and Pattern Recognition(CVPR)2018.
[30] B.KimC.M.Kang,S.H.Lee,H.Chae,J.Kim,C.C.Chung,and J.W. Choi,“Probabilistic vehicle trajectory prediction over occupancy grid map via recurrent neural network,"arXiv preprint arXiv:1704.070492017.
[31] N.Lee,W.Choi,P.Vernaza.C.B.Choy,et al,DESIRE:Distant Future Prediction in Dynamic Scenes with Interacting Agents. IEEE,Jul2017. [Online.Available:http://dxdoi.org/10.1109/CVPR.2017.233[32]K.Fragkiadaki,P.Agrawal,et al,"Learning visual predictive models of physics for playing billiards,"in International Conference on Learning Representations(CLR),2016.
[34] F.-C.Chou,T-H. Lin,HCui,V.RadosavljevicT Nguyen,T.-K. Huang.M.Niedoba,J.Schneiderand N.Djuric,“Predicting motion of vulnerable road users using high-definition maps and efficient convnets," in Workshop on 'Machine Learning for Intelligent Transportation Systems’at Conference on Neural Information Processing Systems(MLITS)2018.
[35] C.M.Bishop,“Mixture density networks,"Citeseer,Tech.Rep,1994[36] S.Lee,SPurushwalkam Shiva Prakash,M.Cogswell,V. Ranjan D.Crandall,and D.Batra,“Stochastic multiple choice learning fo training diverse deep ensembles,"in Advances in Neural Information Processing Systems 29,2016,pp.2119-2127.
[37] C.Rupprecht,I.Laina,R.DiPietro,M.Baust,F.Tombari,N. Navab and G. D. Hager, "Learning in an uncertain world: Representing ambiguity through multiple hypotheses,"in Proceedings ofthe lEEE International Conference on Computer Vision,2017pp.3591-3600[38]N.Deo and M.M.Trivedi,"Multi-modal trajectory prediction osurrounding vehicles with maneuver based lstms,"arXiv preprint arXiv:1805.054992018.
[39] M.Sandler,A.Howard,M.Zhu,A.Zhmoginov,and L.-C.Chen Invertedresiduals and linear bottlenecks:Mobile networks for classifi cation, detection and segmentation,"arXivpreprint arXiv:1801.043812018.
[40] E.A.Wan and R.Van Der Merwe,"The unscented kalman filter for nonlinear estimation,"in Adaptive Systems for Signal Processing Communications, and Control Symposium2000.AS-spcc. The IEEE2000. eee,2000,pp.153-158.
[41] J.Kong,M.Pfeiffer,G.Schildbach,and F.Borrelli,"Kinematic and dynamic vehicle models for autonomous driving control design,"in Intelligent Vehicles Symposium(IV),2015 IEEE. IEEE,2015,Pp1094-1099.
[42] M.Abadi,A.Agarwal,P.BarhamE.Brevdo,et al,“TensorFlow Large-scale machine learning on heterogeneous systems"2015 [Online]. Available:https://www.tensorfloworg/
[43] A.Sergeev and M.D.Balso,“Horovod: fast and easy distributed deep learning in tensorflow,"arXiv preprint arXiv:1802.05799,2018.
[44] D.P.Kingma and J.Ba“Adam:A method for stochastic optimization, arXiv preprint arXiv:1412.6980,2014.
[45] C.Gong and D.McNally,A methodology for automated trajectory prediction analysis,"in AIAA Guidance, Navigation, and Control Conference and Exhibit,2004.
Reproduced from the network, the views in the text are only for sharing and exchange, do not represent the position of this public account, such as copyright and other issues, please inform, we will deal with it in a timely manner.
-- END --