Programmer's Dad Compulsory Course - Take The Baby to Write Games Together

Author: Sun Snow

Source: Python Technology

At home on the weekend, my son is making a fuss about playing games, let's play it, it's not good for health, don't let's play it, can't bear him toss, so I thought, it's better to play a small game together!

He had made up number guessing and dice rolling games before, but now that he was unattractive, he said to him, "Let's play a maze game." ”

Sure enough, I had an interest, so I designed and realized it with him, and now let's see how we do it, maybe we can also become a baby artifact~

Take a sneak peek:

Idea

The maze game, relatively simple, sets up the map, and then uses a recursive algorithm to find the exit and show the process to enhance the fun.

Thinking of the need to involve children together, I chose the drawing program Turtle[1] as an implementation tool.

In this way, you can first draw a maze on paper, and then write into code, let Turtle draw, because the child has drawn with a pen, so when implementing the code, he can fully participate, not only to get the final game, but also to enjoy the production process, develop programming thinking, maybe save a lot of children's programming costs hahaha ~ ~

Start by making a maze with your child, drawing a 5 X 5 small grid on paper, and then, asking him to draw a pathway in the grid, like this:

Draw the maze

Then, convert this map into a maze matrix, with 1 representing the wall and the space representing the path, it should be noted that each edge of the grid is a wall, and the connected part of the wall needs to be opened to become a road.

At this time, you can come with him to achieve, such as letting him use his own blocks and other decorations to set up a maze, and we do digital transformation, and the final transformation result is:

1 1 1 1 1 1 1 1 1 1 1
        1       1 1 1
1 1 1   1   1   1 1 1
1       1   1       1
1   1 1 1   1 1 1   1
1       1   1       1
1 1 1   1   1   1 1 1
1       1   1       1
1   1 1 1   1 1 1   1
1           1 1 1   1
1 1 1 1 1 1 1 1 1   1
           

If the child can't see clearly, you can indicate the path hahaha:

1 1 1 1 1 1 1 1 1 1 1
->_____ 1 _____ 1 1 1
1 1 1 | 1 | 1 | 1 1 1
1 ____| 1 | 1 |___  1
1 | 1 1 1 | 1 1 1 | 1
1 |____ 1 | 1 ____| 1
1 1 1 | 1 | 1 | 1 1 1
1 ____| 1 | 1 |____ 1
1 | 1 1 1 | 1 1 1 | 1
1 |_______| 1 1 1 | 1
1 1 1 1 1 1 1 1 1\|/1
           

After the maze is digitized, it is necessary to represent the maze on the computer.

Turtle was chosen because it will be like drawing with a pen, allowing children to fully participate.

Find a piece of paper, use the maze digitization results just sorted out as a guide to draw, draw a small square when encountering 1, skip when encountering spaces, and draw with your child, mainly to let him experience the rules in the process.

Well, while he draws, let's implement the drawing code.

First of all, you need to know some of the features of Turtle:

1. Turtle's initial coordinates are in the center of the screen, which divides the screen into four quadrants of a flat coordinate system
2. The turtle brush moves in the default minimum unit of one pixel, so the coordinate points need to be initialized
3. The Turtle brush moves relative to the tip, so special attention needs to be paid to the tip orientation

The way to achieve this is the same as the child's strokes, starting with the first grid:

effect

Let's take a look at the code:

def drawCenteredBox(self, x, y, color):
    self.t.up()
    self.t.goto(x - 0.5,    y - 0.5)
    self.t.color('black', color)
    self.t.setheading(90)
    self.t.down()
    self.t.begin_fill()
    for _ in range(4):
        self.t.forward(1)
        self.t.right(90)
    self.t.end_fill()
    update()
           

• DrawCenteredBox is a member method of the maze class Maze, and self refers to the maze class itself, which can be temporarily understood as a global variable
• self.t is an example of a Turtle module, which can be understood as a brush
• The up method means lifting the pen tip
• The goto method is to move to the specified position, where it needs to be moved to the lower left corner of the specified position, so each subtracts 0.5 (the coordinate value conversion is done here, which will be explained later)
• color indicates the set color, the two parameters are the color of the pen and the fill color
• Setheading means to have the nib facing up, that is, to face the nib 90 degrees
• Down means that the tip of the pen is dropped, meaning that the subsequent movement is equivalent to drawing
• begin_fill indicates preparation for padding, i.e. it fills the area drawn from the call to the call end_fill
• Then there is the loop four times, used to draw the square, and within the loop, draw one unit forward (the tip facing) each time, turning 90 degrees to the right, so that a square is drawn
• end_fill is to fill the currently drawn square
• update indicates that the drawing area is updated

See if the process is exactly the same as the child's hand drawing!

Now iterate through the entire maze matrix and keep calling drawCenteredBox to draw the maze:

The code is as follows:

def drawMaze(self):
    for y in range(self.rowsInMaze):
        for x in range(self.columnsInMaze):
            if self.mazelist[y][x] == 1:
                self.drawCenteredBox(x + self.xTranslate, -y + self.yTranslate, 'tan')
           

• rowsInMaze, columnsInMaze represent the rows and columns of a maze matrix
• tan is the color name of desert camouflage[2].

Get out of the maze

The maze is drawn, how to get out?

Ask your child first and ask him to think of a way.

The realization idea is also very simple, that is, to go in one direction, if it is a wall, change the direction, if it is not a wall, continue to walk, and so on...

However, here you can make a rehearsal with the child, such as when the maze is very large, what if you can't remember which roads you have walked?

Exploring a road, not going through, after returning, not remembering which roads were walked, which is a very dangerous thing, if there is a way to remember the path traveled, it would be good.

Here I tell my son about the ancient Greek myths and legends of Theseus vs Minotaur[3], and inspire him to come up with a good way.

How to implement it with code, just mark the path traveled in the maze matrix species:

PART_OF_PATH = 0
OBSTACLE = 1
TRIED = 3
DEAD_END = 4

def search(maze, startRow, startColumn):  # 从指定的点开始搜索
    if maze[startRow][startColumn] == OBSTACLE:
        return False
    if maze[startRow][startColumn] == TRIED:
        return False
    if maze.isExit(startRow, startColumn):
        maze.updatePosition(startRow, startColumn, PART_OF_PATH)
        return True

    maze.updatePosition(startRow, startColumn, TRIED)

    found = search(maze, startRow-1, startColumn) or \
            search(maze, startRow, startColumn-1) or \
            search(maze, startRow+1, startColumn) or \
            search(maze, startRow, startColumn+1)
    if found:
        maze.updatePosition(startRow, startColumn, PART_OF_PATH)
    else:
        maze.updatePosition(startRow, startColumn, DEAD_END)

    return found
           

Because recursive is used, the code is relatively short, let's take a look:

• PART_OF_PATH, OBSTACLE, TRIED, DEAD_END are four global variables that represent pathways, walls, explored paths, and dead paths in the maze matrix, respectively
• The search method is used to explore the maze, accept a maze object, and start location
• Then see if the specified location is a wall, or has been walked through, and if it is an exit
• Then continue exploring, saying that the specified location is marked as having passed
• Next explore in four directions, like west, east, south, and north
• Exploration in each direction is a recursive call to the search method
• If the result of the exploration is that an exit is found, mark the current location as a route, otherwise mark it as a dead end

Here we also need to look at the implementation of the updatePosition method:

def updatePosition(self, row, col, val=None):
    if val:
        self.mazelist[row][col] = val
    self.moveTurtle(col, row)

    if val == PART_OF_PATH:
        color = 'green'
    elif val == OBSTACLE:
        color = 'red'
    elif val == TRIED:
        color = 'black'
    elif val == DEAD_END:
        color = 'red'
    else:
        color = None

    if color:
        self.dropBreadcrumb(color)

def moveTurtle(self, x, y):
        self.t.up()
        self.t.setheading(self.t.towards(x+self.xTranslate, -y+self.yTranslate))
        self.t.goto(x+self.xTranslate, -y+self.yTranslate)

def dropBreadcrumb(self, color):
    self.t.dot(color)
           

• The updatePosition method itself is not complicated, first marking the maze matrix, then moving the tip of the pen to the specified point, and then determining the value of the marker, drawing points on the specified point
• The method of movement is to moveTurtle, first lifting the nib and then turning the tip of the pen towards the point that will be moved past
• Turtle's towards method calculates an angle between the current point of a pen tip and the specified point, which is used to turn the tip towards the point to be moved past, where xTranslate and yTranslate are the offsets of pixels in the coordinate system (as explained later)
• Turtle's dot method works by drawing a point

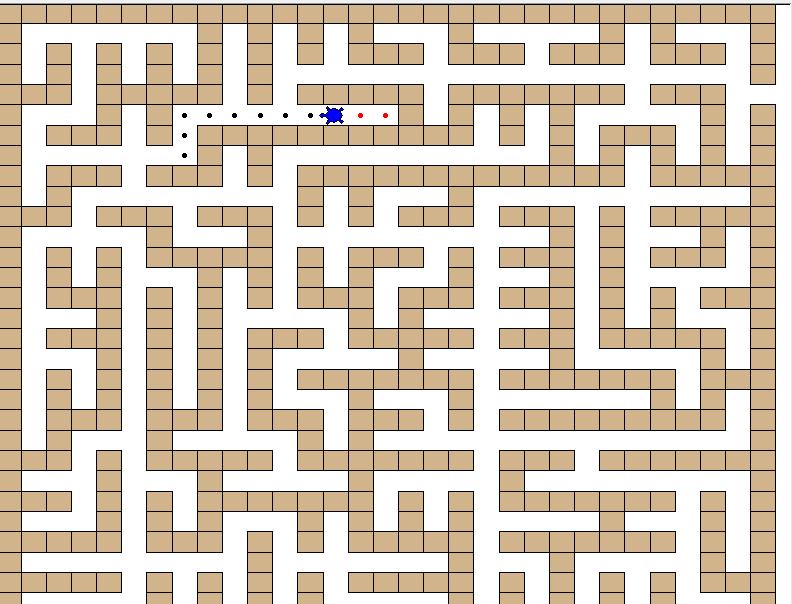
Take a look at the effect:

Bigger challenges

When the child sees the maze he made and is walked out by the little turtle, don't mention how happy he is.

It didn't take long, though, to want a more complex maze, a maze with multiple branches.

Obviously there are manual ways that are a bit difficult and boring. You need to let the program automatically generate the maze.

Originally wanted to do a big job, suddenly thought of a maze article written by Doudou before [4], look for it, just have a maze generation algorithm, great.

For information on how to dynamically generate a maze, please participate in the Beanie article, which has detailed instructions

After analyzing the code, the labyrinth class was ported over, and the result generated was imported into the maze class written by the author, and the maze scale was set to 100 X 100, which shocked:

Giant maze

Watching the little turtle waddle through the huge maze, there is also an inexplicable sadness

With the Maze Spawn tool, there's a lot of fun:

• How to make the turtle find the way out faster
• How to get turtles to randomly appear in the maze
• How to dynamically set the entrances and exits of the maze
• ……

We have achieved these problems one by one, and the children have actively participated in the whole process, and from time to time they are dancing and happy because of good ideas...

Interested readers can reply to keywords, get source code, research solutions, and look forward to talking to you.

About coordinate system settings

There are a few pits left in front, it is about the Turtle coordinate system, and it is explained here.

The first question is the coordinate unit

By default, Turtle's coordinate unit is one pixel, if you want to zoom in on the display of Hua, you need to calculate how many pixels the unit we use is equivalent to, and then every time you calculate the coordinates, you have to take into account this value, when the real area changes, you have to adjust this value, very troublesome, and easy to make mistakes.

So Turtle provides a way to set our own coordinate units, setworldcoordinates, which accepts four parameters, namely the x-coordinate and y-coordinate of the point in the lower left corner of the coordinate system, and the x-coordinate and y-coordinate of the upper right corner.

If the lower left corner is set to (-5, -5) and the upper right corner is set to (5, 5), Then Turtle will set the coordinate origin in the center of the screen and split the screen into squares of 10 X 10, each block with a side length equivalent to one coordinate unit, that is, when we say move the tip of the pen to (3, 4) this coordinate point, Turtle will move three units from the center of the screen to the right and then up by 4 units.

This makes it very convenient, regardless of the screen size, pixel size, Turtle will follow our instructions and make the correct response.

Another problem is the two offsets xTranslate and yTranslate

They are calculated as follows:

self.xTranslate = -columnsInMaze/2
self.yTranslate = rowsInMaze/2
           

The meaning of existence is to convert from row and column values to the values of the Turtle coordinate system, such as in row and column notation, (0, 0) point, in our transformed 10 X 10 coordinate system, the corresponding coordinate point is (-5, 5).

Because it is convenient to use the row and column notation when looking up data, it is more convenient to represent it in a coordinate system with the origin as the reference.

summary

Well, the maze about the turtle implementation is introduced here, just a simple description of the implementation ideas, and the child's interaction, the code implementation also needs details and problems, limited to space, not expanded, interested readers can download the source code, run and try, maybe more interesting ideas, welcome to communicate in the comments.

We learn code not only to solve problems and get work done, but more often than not, we can also use entertainment and companionship with children, in this process, to give children not only companionship, but also the way to deal with problems, and the attitude of life.