Ladies and gentlemen, young and old! In the next zhang big less.
Alternating ornaments made by Celtic scribes and stonemasons have fascinated people for many centuries. These designs, ranging from individual knots to elaborate ornaments made up of many motifs, provide a rich source of examples for geometrically minded mathematicians. Many aspects of interlaced patterns can be studied mathematically, and some of them will be explored in this article. Let's start with the geometry of knots.
Build interlaced patterns
The basis of many Celtic knot patterns is the lattice. It is this lattice that gives the Celtic knots a unique proportion. It usually consists of squares, but occasionally it also consists of rectangles of 3×4. For ease of reference, we can think of this lattice as a combination of two dual lattices with mesh size twice the size of the original lattice (Figure 1b). These meshes will be called auxiliary meshes. When laying out the design, only the vertices of these two meshes are drawn in (Figure 1c).
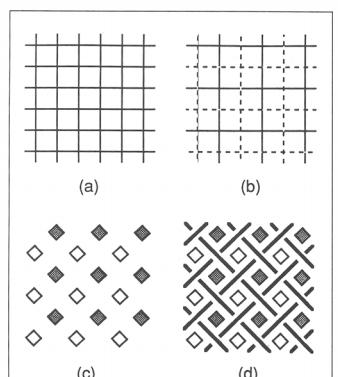
Figure 1. How to build an interlaced braid pattern
The knotting methods created on these grids are all related to braid weaving, which is the basic weaving pattern used for basket weaving and other crafts, as shown in Figure ld. Notice that the intersections in the pattern are at the intersection of the two auxiliary meshes, and the staggered arrangement has an interlaced nature. Each line is staggered up and down. This is also a feature of Celtic motifs, although one or two anomalies are known (Figure 2).
Figure 2: A non-interlaced Celtic pattern
In Egyptian, Greek and Roman ornaments, as well as in the art of many other cultures, interwoven patterns of partial weaving can be found. For the Celts, however, these alternating braids were merely the raw material for the artist to begin his creations. In order to obtain a more elaborate interlaced design, the regularity of this original pattern must be broken. This is achieved by breaking the two strings at the intersection and reconnecting the ends, as shown in Figure 3. (This operation is currently used in combinatorial knot theory.) Note that eliminating crossovers in this way preserves the alternating properties of interlacing. When enough crosses are removed, the braids underneath are no longer the main features in the design, and a pattern consisting of knot patterns appears. In this way, dazzling staggered designs can be created.
Figure 3: Rules for eliminating crossovers
So far, the only accessibility tool for layout design is the vertices of the secondary raster. An extra construction line is drawn between these vertices to indicate which intersections will be removed from the braid and how to reconnect the ends. These lines are called breakpoint markers. Each breakpoint marker is an edge of one of the auxiliary rasters. At each intersection of the braid, there are two such edges, and the selected edge indicates which of the two possible reconnections to use. A glance at the example in Figure 4 will clearly see the convention.
Figure 4: The break marker helps with construction by indicating how the intersection point breaks.
To complete the design, the path of the strip is outlined and the background is filled in. This masks all the structural lines. Patterns are then interwoven to produce a characteristic interlaced weave. Figure 5 illustrates the construction of some elemental knot patterns.
Figure 5: Examples of interlaced patterns and their structure.
Eliminating crossovers according to the simple rules shown in Figure 3 doesn't always have an aesthetically pleasing effect. Sometimes, if the path of the line is allowed to deviate from the path of the braid, better results are obtained. Where two break marks intersect to form a corner point, the path of the string can also be angled. This has been done in the drawings. In other cases, fairly sharp bends can be replaced with softer curves to produce a more elegant, fluid design. Figures 7 and 8d show several arcs of different curvatures. These modifications helped to further disguise the underlying woven structure on which the design was based. Another variation produced a very fine form of interweaving: the two edges of a ribbon often thought to be interweaved were themselves used as interwoven ropes. An example of this "two-line interweaving" is shown in Figure 8j.
Once people learned about the techniques used to make Celtic ornaments, the art itself lost some of its mystery. Copying ancient designs and creating your own becomes fairly accurate and easy. (Don't be surprised if you find your work elsewhere, though.) )。 Any area of a straight line can fill the nodes by treating their boundaries as if they were made up of breakpoints on a suitable mesh (see Figure 6a). It is also possible to map the pattern to the curved area by dividing the pattern into quadrilaterals (Figure 6b).
Figure 6: Irregularly shaped panels can be decorated using the same technique.
Although this construction procedure may seem simple, the idea that the Celtic interlaced patterns were related to the braiding craft matured over the years. The methods used by the Celts themselves are no longer known, and the technique was developed by J. Romilly Allen when he investigated the patterns of the British Isles at the turn of the century. He recorded page xvii[1].
The theory that the Celts evolved from weaving is entirely original, and although it is simple to explain, I spent quite 20 years thinking about it while classifying patterns.
When we think of the braids at the bottom that can be modified a lot and are easy to mask, maybe that's not so surprising.
Figure 7: This pattern is not based on a standards grid.
Interpret Celtic design as a trim
Many Celtic knots are striped, either as part of a border or simply as a narrow rectangular panel. In many such ribbon patterns, the crossover is systematically eliminated, and the pattern of the break marker is repeated at regular intervals. This creates a pattern that can be described as "local periodicity": a single theme is repeated side by side. In other forms of ornamentation, this periodicity produces translational symmetry when the pattern is seen as a randomly selected segment on an infinite strip. In knotting, however, the transition from a small part to an idealized relief is not so immediate. In other forms of decoration, the pattern is simply truncated when it reaches the edge of the available space, and knotting rarely ends so abruptly. The pattern is adapted so that the otherwise free ends are joined together to form a continuous harness.
In this article, the knot pattern is seen as a frieze in the traditional mathematical sense: as part of the pattern, it extends infinitely in both directions. In the underlying lattice, the pattern is defined by two parallel break marker lines, and the arrangement of the other break points gives the pattern overall translational symmetry. Some examples are shown in Figure 8. The first two patterns are not built on a standard lattice. The pattern in Figure 8a is thought to be Scandinavian. Like the triangle pattern used in Figure 8b, it is usually arranged in four groups to form a square pattern. Figure 7 shows an example based on the same pattern. I ruled out patterns that could be split into other patterns. For example, if the knot design in FIG. 2 is converted into a ribbon, the resulting pattern consists of two parallel patterns, and the two patterns are not compatible. If the non-interlaced paths of an interlaced pattern (or equivalent to a projection linked on the image plane) are connected, then it can be said that it is connected. The frieze constructed from Figure 2 is not connected. For now, I will assume that these friezes are connected, and that the concept of connectivity captures to some extent our intuitive understanding of when a pattern can be split. However, we will return to this question of separability later.
Figure 8: An example of a Celtic band pattern
Symmetry of the interlaced frieze
According to the symmetry operation, the symmetrical properties of the frieze pattern can be mathematically analyzed: an equidistant diagram that carries the pattern onto itself. As we all know, a plane has four equidistant planes: rotation, translation, reflection, and slip reflection. For a flat ribbon pattern, the only possible symmetries are 2-fold rotation, centerline reflection, reflection perpendicular to centerline, and slip reflection along centerline. These symmetries can be combined in different ways, but due to the rigidity of the geometry, the number of combinations is limited to 7. An example of a pattern showing these seven different symmetrical types is shown in Figure 9.
Fig. 9: Seven one-sided band patterns
When comparing the kink bands to these flat patterns, it is clear that we cannot interpret the two patterns in the same way. Interlaced patterns are not limited to flat surfaces. At the intersection, the rope seems to extend front and back of the frame. The three-dimensional object we perceive is made up of continuous ropes located near a plane, rather than a collection of arcs located within a plane. We want to see the front pattern on the back.
Interpreting the interlaced frieze as a three-dimensional pattern means that there are additional isometric lines that can act as symmetry. Two of these are compound motions, such as slip reflections: a spiral is a rotation that then translates along its axis; rotational reflection refers to rotation and reflection on a plane perpendicular to the axis. Both of these isometrics can serve as symmetry for interlaced patterns.
The complete set of possible symmetries of a double-sided frieze is described by reference to a set of standard axes: the a-axis extends along the belt, the b-axis is located within the band plane perpendicular to a, and the c-axis is perpendicular to the band. Possible symmetries are 2-fold rotation around any of the three axes, reflections in planes that are orthogonal to each of the three axes, slip reflections in planes that are orthogonal to a and b, spiral movements along a, and 2-fold rotational reflections around c. This final symmetry is the same as the reflection in the point or inversion (since it is 2-fold symmetry).
These symmetries can be combined in many different ways. Since these double-sided straps are less familiar than the seven single-sided straps, figure 10 shows patterns illustrating the 31 symmetrical types. The pattern in each pattern is a positive triangle, and in most cases it is black on one side and white on the other. When the reflection on the ribbon plane is a symmetry, then both sides of the triangle must be the same color: in this case, the color of the triangle is gray. Next to each pattern is a label in the form P[313U], which encodes the symmetry present in the pattern. After the symbol P (which indicates that the pattern is periodic in one direction), the symbols 2,2', 2,m, and a are used to represent the normal vectors of the 2-fold axis of rotation, the 2-fold spiral, the 2-fold rotational reflection, or the mirror plane or the gliding plane coincides with one of the reference axes. The first, second, and third symbols after P correspond to the a-axis, the b-axis, and the c-axis, respectively. If an axis and a symmetry plane coincide with the same reference axis, two symbols are given; if there is no symmetrical element corresponding, the position marker is used with symbol I.
Fig. 10: 31 double-sided band patterns.
Trying to determine which symmetries exist in a particular knot pattern is not easy. Readers are encouraged to try the pattern in Figure 8. A useful observation is that the intersections of the Celtic frieze all have the same arrangement, and they have two kinds. In addition, each one is stabilized by all 2 rotations (see Figure 11). Thus, direct symmetry intersects with homogeneous symmetry; indirect symmetry interchanges the two symmetries.
Figure 11: Both rotations preserve the crossing.
After analyzing a few examples, one would ask how many bilateral groups could be generated from a Celtic knot pattern. Can they all happen? If not, then which ones? It is also possible to consider the problems that actually occur in practice.
The seven "gray groups"—those with the image plane as the element of symmetry—do not appear on the knot pattern because the intersections do not conform to this symmetry. Thus, we can eliminate all groups whose label m is part of the last symbol. Observe that almost all of the staggered decorations are alternating, so that more groups can be eliminated.
Suppose the pattern of a knot has mirror symmetry. An example is shown in Figure 12a. In order to convert this knot into an alternating knot, it is necessary to add an additional strip located on the mirror surface, as shown in Figure 12b. Those groups containing reflections on planes that are orthogonal to the a-axis cannot arise from interlaced knot patterns, because the bands located in the mirror plane run directly from the top edge of the band to the bottom —they can never be connected to anything else. Thus, groups where the label has an m in the first position cannot be found in the Celtic motif. The "m" in the label is part of a second symbol that can be produced from an alternating pattern: this pattern must have a strip that goes straight along the centerline. There are two of these groups. p1m1 and p121. They are marked with (t) in Figure 10. However, this form of pattern is inconsistent with the standard Celtic grid, so these symmetry groups cannot appear in Celtic patterns either.
Figure 12: Patterns with bilateral symmetry can be alternately made by adding additional lines.
There is also a class of group tags that can be eliminated: those that contain a as part of the third symbol (indicating that the drawing plane is also a slip plane). The reason for this is that in order to create an alternating design, it is necessary to have straight lines pass through the straps, as in the case of Pm[3D], and these lines can never connect with anything.
There are also 10 possibilities. These possibilities are marked with an asterisk (*) in Figure 10. Figure 8 shows an example of a Celtic pattern showing these symmetrical groups. In the ancient designs I was able to find, I adopted them; some of them were my own creations.
The relative richness of symmetry types
When I looked for examples of Celtic designs, I found that the richness of different symmetry types varied greatly. Some groups (Pl12, P222, P2'22) are very common; others are rare. In fact, the only pattern I could find with the P1a1 group was not built on the standard grid mentioned above. For the P112 and P121 groups, I didn't find any examples at all. Are there any features of these patterns that make them difficult to obtain?
Before solving this dilemma, we have to consider another problem. Is there a correlation between the (two-sided) symmetry group of the interlaced design and the (one-sided) symmetry group of its underlying fracture marker pattern? The answer to this question is yes. To know why, note that the non-interlaced paths of the chords and the distribution of the break marks have the same symmetry type. The corresponding series is shown in Table 1. Observing how each of the three rare groups pairs is paired with another seems to be the first choice. In fact, this preference is not a choice made consciously or unconsciously by the designer. It is the result of the fact that the ancient motifs ended, not the real frieze.
Study the two bands in Figure 13. Have you noticed any difference? Structurally, they are the same; in terms of symmetry, they are not the same. This is easiest to see at the edges. In Figure 13b, the outermost intersections are relative; in Figure 13a, they are staggered, with intersections on one side located between intersections on the other side. Therefore, the symmetry types of the two braids are different.
Figure 13: Braided alternately with five and six threads
The symmetrical type of the woven frieze depends on its width. Those lattices with an even number of lattice elements between the two edges have symmetric type P222 those braids that span odd cells have p121 type. This observation allows us to unravel the mystery of the missing population. It also provides an alternative way to enumerate Celtic groups; because eliminating crossovers only breaks symmetry, the Celtic group must be a subgroup of P222 or p121.
Table 1 can now be improved to show how the symmetry type depends on the width of the frieze and the underlying markings. The results are shown in Table 2. Now we have at most one group in each box of the table. The type of interlaced symmetry is determined entirely by the geometry of the underlying fracture markers. In addition, all rare groups are associated with bands of odd widths. The only band I found with odd widths is shown in Figure 8d. Its symmetrical type is P121 – a group independent of the width of the frieze.
It's not hard to see why straps of odd widths are uncommon. This is not as suggested [1, p. 260], and the pattern looks unbalanced. Instead, this is related to the fact that the original Celtic motif was a limited design with no scatter heads. At the end of a row of patterns, the lines are paired and joined together — a process that requires an even number of lines. The number of lines is related to the width of the frieze: the parity of the width is equal to the parity of the number of lines. The Celts could only use friezes of odd widths while ensuring continuity, for example in full boundaries. In some places, loose endings occur naturally. These usually appear in animal forms: strange creatures with elongated tails, limbs, necks or tongues intertwined in strange ways. However, these patterns are never large enough to have duplicate patterns, so no example of a frieze is provided.
Continuity, transitivity and divisibility
One of the problems faced by designers of interlaced patterns is how to determine the number of parts in the finished design. In the early forms of Celtic ornamentation, it was clear that the continuity of the path was sought. This is important as a symbol of eternity. Even in extremely complex patterns, only one line is arranged in endless loops. In some examples, the regularity of the pattern is deliberately abandoned and the pattern is modified to ensure a unique path. In later eras, this rule was observed less strictly, but loops in the pattern were still avoided. This raises the question of whether there is an easy way to determine the number of bands in a design from the basic pattern of the break mark.
When the interweaving is a woven rectangular part (Figure 14), then the answer can be represented by a bounding rectangle. If the lattice under the braid contains n×Rn elements, the pattern will have a single component if h .c.f. (m,n)~2.If the pattern is square (n=m), the number of components is [1/2n]. In fact, if we calculate the closed loop instead of the component, then the digital I/2n can be considered correct. When breakpoint markers are added and the weave is split, these rules are no longer valid. What rules replaced them?
Figure 14: Can the number of components in a rectangle pattern be determined based on the dimensions of the rectangle?
What about staggered friezes: how many lines do they have? The pattern in Figure 8f is a chain of infinitely many closed loops. All other straps in Figure 8 have a finite number of infinitely long strips. Most of the patterns from the Celts have even lines; only the non-standard patterns a and b, and the l, m, and n I designed in Figure 8 have a line; Figure 8d has three lines.
For patterns with multiple components, we can investigate whether the symmetry group acts as a transport to the strips: can each strip be carried to any other strip by some symmetry of the pattern? In layered patterns and fabric backgrounds, the patterns transmitted by the lines are called isoline patterns. Using this term, we can say that in the pattern in Figure 8, c and e are not equivalent, and by translation, all other modes except i and j are equivalent. In cases i and j, rotation is required to achieve full transitivity.
There is a simple test to check whether the interlaced frieze patterns are equal. The builder link is constructed by connecting the two ends of the basic area of the frieze together. If the chain has only one component, then the translated band is equivalent.
Another question that arises in mathematical studies of fabrics is determining whether a layered pattern will spread out: can these lines be divided into two or more groups of disconnected threads? Above we assume that the friezes are connected. One consequence of this is that Celtic's staggered friezes never fall apart. If an interlaced frieze is alternating, connected and separable, so is the chain of goods formed by it. However, if and only if the link is not connected, the alternating diagram of the link represents a separate link [4].
Finer classification
At some point, it is less satisfactory to divide the numerous Celtic interlaced patterns into 10 categories, especially when we realize that the resulting three-dimensional symmetrical type is entirely determined by the two-dimensional fracture marker pattern at the bottom. It would be nice to be able to sort by pattern type[3] rather than just by symmetry type.
Intuitively, a pattern is a collection of patterns arranged in a systematic manner. This regularity is mathematically simulated by requiring the symmetry group of the pattern to transit the pattern. Classification by pattern type depends on three factors: the symmetry group G of the pattern; the stabilizer stabG (M) of pattern M; and the collection of pattern transitivity subgroups of G.
However, when we tried to apply this analysis to Celtic friezes, we immediately ran into difficulties: patterns are not discrete, so there is no obvious or natural way to divide them into patterns. The continuity of strings makes it impossible to select a pattern in an explicit manner, and the choices made will affect the final pattern type. Ironically, the arrangement of break marks associated with the interlaced frieze pattern is discrete, but not necessarily transitional.
End
In this study of Celtic knots, I focused on a particular topic: symmetry. Analysis of symmetry is possible, in part because of the lattice structure behind the design structure. This inherent regularity and the cyclicality imposed by the artist mean that many of the motifs have extraordinary symmetry. Readers may feel that the same rigidity leads to a boring art form. A non-mathematician confronted with the mathematical classification of patterns according to symmetrical types writes [2,p.70],
There is no danger that the pattern maker's resources will be depleted by the constraints of the geometry.
In this case, this sentence also seems appropriate. A glance at the Celtic manuscripts makes it easy to believe that the geometric framework does not hinder the artist's creation in the slightest. Imagination and creativity still have room to express themselves.
bibliography
1. J. Romilly Allen,Celtic Art in Pagan and Christian Times,London: Methuen (1904).
2. E. H. Gombrich,The Sense of Order: a study in the psychology of decorative art,Ithaca, NY: Cornell University Press (1979).
3. B. Gr~nbaum and G. C. Shephard,Tilings and Patterns,New York: Freeman (1987).
4. W. W. Menasco, Closed incompressible surfaces in alternating knot and link complements. Topology23 (1984), 37-44.
5. A. V. Shubnikov and V. A. Koptsik,Symmetry in Science and Art(translated from the Russian by G. D. Archard), New York: Plenum (1974).