女士們,先生們,老少爺們兒們!在下張大少。
凱爾特抄寫員和石匠制作的交錯裝飾物,許多世紀以來一直讓人着迷。這些設計,小到單個的結,大到由許多圖案組成的精心設計的飾片,都為具有幾何思維的數學家提供了豐富的執行個體來源。交錯圖案的許多方面都可以用數學來研究,本文将對其中一些進行探讨。我們從繩結的幾何學開始。
建構交錯圖案
許多凱爾特繩結圖案的基礎是格子。正是這種格子賦予了凱爾特繩結獨特的比例。它通常由正方形組成,但偶爾也會由3×4的長方形組成。為了便于參考,我們可以把這個格子看作是兩個對偶格子的結合體,其網眼大小是原始格子的兩倍(圖1b)。這些網格将被稱為輔助網格。當布置設計時,隻有這兩個網格的頂點被畫進去(圖1c)。
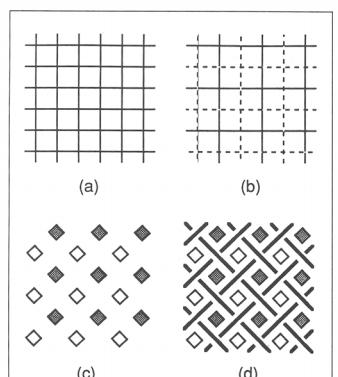
圖1. 如何建構交錯的辮子圖案
在這些網格上創造的結法都與辮子編織有關,辮子編織是用于籃子編織和其他工藝品的基本編織模式,如圖ld。請注意,圖案中的交叉點位于兩個輔助網格的交叉點上,而且交錯排列有一種交錯的性質。每根線都上下交錯。這也是凱爾特圖案的一個特點,盡管有一兩個異常情況是已知的(圖2)。
圖2:一個非交錯的凱爾特圖案
在埃及、希臘和羅馬的裝飾品以及許多其他文化的藝術中,都可以找到由部分編織而成的交織圖案。然而,對于凱爾特人來說,這些交替的辮子僅僅是藝術家着手創作的原材料。為了獲得更精細的交錯設計,必須打破這種原始圖案的規律性。這是通過在交叉處打斷兩個字元串并重新連接配接兩端來實作的,如圖3所示。(目前在組合紐結理論中使用這樣的操作。)請注意,以這種方式消除交叉會保留交錯的交替屬性。當足夠多的交叉被去除時,下面的辮子不再是設計中的主要特征,由結圖案組成的圖案出現了。通過這種方式,可以創造出令人眼花缭亂的交錯設計。
圖3:消除交叉的規則
到目前為止,布局設計的唯一輔助工具是輔助栅格的頂點。在這些頂點之間繪制額外的構造線,以訓示哪些交叉點将從辮子中移除以及如何重新連接配接兩端。這些線稱為斷點标記。每個斷點标記都是其中一個輔助栅格的一條邊。在編結的每個交叉點,都有兩條這樣的邊,所選擇的邊表示要使用兩種可能的重新連接配接中的哪一種。看一眼圖4中的示例,就會清楚地看到約定。
圖4:斷開标記通過訓示交叉點如何斷開來幫助構造。
為了完成設計,條帶的路徑被勾勒出來,背景被填上。這掩蓋了所有的結構線。然後圖案交織在一起,産生特有的交錯編織。圖5說明了一些元素結圖案的構造。
圖5:交錯圖案的例子和它們的結構。
根據圖3所示的簡單規則消除交叉并不總是産生美觀的效果。有時,如果允許線的路徑偏離辮子的路徑,則會獲得更好的結果。在兩個折斷标記相交形成角點的地方,也可以使弦的路徑成角度。在附圖中已經做到了這一點。在其他情況下,可以用更柔和的曲線來代替相當尖銳的彎曲,以産生更優雅、流暢的設計。圖7和圖8d顯示了幾種不同曲率的圓弧。這些修改有助于進一步掩飾設計所基于的底層編織結構。另一種變化産生了一種非常精細的交織形式:通常被認為是交織的絲帶的兩個邊緣本身就被用作交織的繩子。圖8j中示出了這種“雙線交織”的一個例子。
一旦人們了解了制作凱爾特裝飾品的技術,這項藝術本身就失去了一些神秘性。複制古代的設計并創造出你自己的設計變得相當準确和容易。(不過,如果你在其他地方發現了你的作品,也不要感到驚訝。)。任何直線區域都可以通過将其邊界視為由合适網格上的斷點組成來填充結點(參見圖6a)。通過将圖案劃分為四邊形,也可以将圖案映射到曲線區域(圖6b)。
圖6:不規則形狀的嵌闆可以使用相同的技術進行裝飾。
盡管這種構造程式看起來很簡單,但凱爾特人的交錯圖案與辮子工藝有關的想法經過多年才成熟。凱爾特人自己使用的方法已不為人知,上述技術是J.Romilly Allen在世紀之交調查不列颠群島的圖案時開發的。他記錄了[1]的第xvii頁。
凱爾特人從編織中進化而來的理論完全是原創的,盡管解釋起來很簡單,但我花了相當20年的時間來思考,同時對圖案進行分類。
當我們想起底層的辮子可以進行大量的修改,而且很容易被掩蓋,也許這就不那麼令人驚訝了。
圖7:這種圖案不是基于标準的網格。
将凱爾特設計解讀為飾帶
許多凱爾特結都是條狀的,要麼作為邊框的一部分,要麼簡單地作為一個狹窄的矩形嵌闆。在許多這樣的帶狀圖案中,系統地消除了交叉,并且以規則的間隔重複中斷标記的圖案。這就産生了一種可以被描述為“局部周期性”的模式:一個單一的主題被并排重複。在其他形式的裝飾中,當圖案被視為無限長條上随機選擇的一段時,這種周期性會産生平移對稱。然而,在打結中,從一小部分到理想化的浮雕的轉變并不是那麼立竿見影的。在其他形式的裝飾中,當圖案到達可用空間的邊緣時,圖案會被簡單地截斷,而打結很少會如此突然地終止。該圖案被适配,使得原本自由的末端連接配接在一起以形成連續的線束。
在這篇文章中,繩結圖案被視為傳統數學意義上的飾帶:作為圖案的一部分,在兩個方向上無限延伸。在底層格子中,圖案被兩條平行的斷裂标志線所限定,其他斷裂點的排列使圖案整體上具有平移對稱性。一些例子顯示在圖8中。前兩個圖案不是在标準格子上建構的。圖8a中的圖案被認為是斯堪的納維亞的。像圖8b中使用的三角形圖案,通常以四組排列形成方形圖案。圖7顯示了一個基于相同圖案的例子。我排除了可以分割成其他圖案的圖案。例如,如果将圖2中的結設計轉換成飾帶,所産生的圖案由兩個平行的圖案組成,而這兩個圖案是不相通的。如果一個交錯的圖案的非交錯路徑(或者等同于連結在圖像平面上的投影)是連接配接的,那麼就可以說它是連接配接的。由圖2建構的飾帶是不相連的。目前,我将假設這些飾帶是連接配接的,并且連接配接性的概念在一定程度上抓住了我們對圖案何時可以被分割的直覺了解。然而,我們将在以後回到這個可分離性的問題上。
圖8:凱爾特飾帶圖案的例子
交錯飾帶的對稱性
根據對稱運算,可以在數學上分析飾帶圖案的對稱性質:将圖案承載到自身上的等距圖。衆所周知,平面有四個等距面:旋轉、平移、反射和滑移反射。對于平面飾帶圖案,唯一可能的對稱是2重旋轉、中心線反射、垂直于中心線的反射以及沿中心線的滑移反射。這些對稱性可以用不同的方式組合,但是由于幾何形狀的剛性,組合的數量被限制在7個。展示這七種不同對稱類型的圖案示例如圖9所示。
圖9:七個單側飾帶圖案
當把扭結飾帶與這些平面圖案進行比較時,很明顯我們不能用同樣的方式來解釋這兩種圖案。交錯圖案并不局限于平面。在交叉處,繩子似乎在畫面的前後延伸。我們感覺到的三維物體是由位于平面附近的連續繩子組成的,而不是位于平面内的弧的集合。我們希望看到背面的正面圖案。
将交錯的飾帶解釋為三維圖案意味着有額外的等距線可以作為對稱。其中兩個是複合運動,比如滑移反射:一個螺旋是一個旋轉,然後沿着它的軸平移;旋轉反射是指在垂直于軸的平面上的旋轉和反射。這兩種等距都可以作為交錯圖案的對稱。
通過參考一組标準軸來描述雙面飾帶的可能對稱的完整集合:a軸沿着帶延伸,b軸位于垂直于a的帶平面内,c軸垂直于帶。可能的對稱是圍繞三個軸中的任何一個軸的2重旋轉,在與三個軸中的每一個軸正交的平面中的反射,在與a和b正交的平面中的滑移反射,沿着a的螺旋運動,以及圍繞c的2重旋轉反射。這最後的對稱與點或反轉中的反射相同(因為它是2重對稱)。
這些對稱性可以有許多不同的組合方式。由于這些雙面飾帶不如七種單面飾帶熟悉,圖10中顯示了說明31種對稱類型的圖案[5]。每個圖案中的圖案都是一個正三角形,在大多數情況下,它的一邊是黑色的,另一邊是白色的。當在帶狀平面上的反射是一種對稱時,那麼三角形的兩邊必須是相同的顔色:在這種情況下,三角形的顔色為灰色。每個圖案旁邊都有一個形式為P[313U]的标簽,它編碼了圖案中存在的對稱性。在符号P(表示圖案在一個方向上是周期性的)之後,符号2、2'、2、m和a被用來表示2重旋轉軸、2重螺旋、2重旋轉反射、或鏡像平面或滑行平面的法向量與其中一個參考軸重合。P後面的第一個、第二個和第三個符号分别對應于a軸、b軸和c軸。如果一個軸和一個對稱平面與同一參考軸重合,則給出兩個符号;如果沒有對稱元素對應,則用符号I作為位置标記。
圖10:31種雙側飾帶圖案。
試圖确定特定結模式中存在哪些對稱性并不容易。鼓勵讀者嘗試圖8中的模式。一個有用的觀察是凱爾特飾帶的交叉點都有相同的排列,它們有兩種。此外,每一種都通過所有的2重旋轉來穩定(見圖11)。是以,直接對稱與同類對稱交叉;間接對稱将兩種對稱互換。
圖11:這兩次旋轉都保留了交叉。
在分析了幾個例子之後,有人會問,有多少個雙側群可以從凱爾特結圖案中産生。它們都可能發生嗎?如果不是,那麼是哪些呢?還可以考慮在實踐中實際發生的問題。
七個“灰色組”——那些以圖檔平面為對稱元素的組——不會出現在結圖案上,因為交叉點不符合這種對稱性。是以,我們可以消除其标簽的m作為最後一個符号的一部分的所有組。觀察到幾乎所有的交錯裝飾都是交替的,這樣就可以消除更多的群。
假設一個結的圖案具有鏡像對稱性。圖12a中顯示了一個例子。為了将這個結轉化為交替結,有必要增加一條位于鏡面上的額外的條帶,如圖12b所示。那些包含在與a軸正交的平面上的反射的組不能從交錯的結模式中産生,因為位于鏡像平面上的條帶會直接從帶子的頂部邊緣跑到底部——它們永遠不可能與其他東西連在一起。是以,那些标簽在第一位置有一個m的組不能在凱爾特人圖案中找到。标簽中的 "m "是第二個符号的一部分,可以從交替圖案中産生:這種圖案必須有一根條帶沿着的中心線直走。這些群有兩個。p1m1和p121。它們在圖10中用(t)标記。然而,這種形式的圖案與标準的凱爾特人的網格不一緻,是以這些對稱群也不能出現在凱爾特圖案中。
圖12:可以通過添加額外的線來交替制作具有雙側對稱性的圖案。
還有一類群組标簽可以消除:那些包含a作為第三個符号的一部分的标簽(表示圖畫平面也是一個滑移平面)。這樣做的原因是,為了創造一個交替的設計,必須像在Pm[3D的情況下一樣,讓直的線穿過帶子,而這些線永遠不可能與任何東西連接配接起來。
還有10種可能性。這些可能性在圖10中用星号(*)标記。圖8顯示了展示這些對稱組的凱爾特圖案的例子。在我能夠找到的古代的設計,我就采用了它們;有一些是我自己的創作。
對稱性類型的相對豐富程度
在我尋找凱爾特人設計的例子時,我發現不同對稱類型的豐富程度有很大的不同。有些組别(Pl12、P222、P2'22)非常常見;有些則很罕見。事實上,我所能找到的唯一具有P1a1群的圖案并不是在上述的标準格子上建構的。對于P112和p121這兩個組别,我根本沒有發現任何例子。這些圖案是否有什麼特點使它們難以獲得?
在解決這個難題之前,我們要考慮另一個問題。交錯設計的(兩面)對稱性群與它的底層斷裂标志圖案的(一面)對稱性組之間是否有關聯?這個問題的答案是肯定的。要知道為什麼,請注意弦的非交錯路徑和斷裂标記的分布具有相同的對稱性類型。對應關系列于表1。觀察一下三組稀有組中的每一組是如何與另一組配對的,這似乎是優先選擇。事實上,這種偏愛并不是設計者有意識或無意識地做出的選擇。它是古代圖案終止的事實的結果,而不是真正的飾帶。
研究圖13中的兩段飾帶。你注意到有什麼不同嗎?從結構上看,它們是一樣的;從對稱性上看,它們是不一樣的。這一點在邊緣處最容易看到。在圖13b中,最外層的交叉點是相對的;在圖13a中,它們是交錯的,一條邊上的交叉點位于另一條邊上的交叉點之間。是以,這兩個辮子的對稱性類型是不同的。
圖13:用五根和六根線交替編成的辮子
編織飾帶的對稱類型取決于它的寬度。在兩條邊之間具有偶數個晶格單元的那些晶格具有對稱類型P222那些跨越奇數個單元的辮子具有p121型。這一觀察結果讓我們解開了失蹤群體的謎團。它還提供了一種列舉凱爾特群的替代方法;因為消除交叉隻會破壞對稱性,是以凱爾特群必須是P222或p121的子群。
現在可以對表1進行改進,以顯示對稱類型如何取決于飾帶的寬度以及底層标記。結果顯示在表2中。現在我們在表的每一個方框中最多有一個組。交錯的對稱性類型完全由底層斷裂标記的幾何形狀決定。此外,所有罕見的組别都與奇數寬度的飾帶有關。我發現的唯一有奇數寬度的飾帶在圖8d中顯示。它的對稱類型是P121——一個與飾帶的寬度無關的組别。
不難發現為什麼奇數寬度的飾帶不常見。這并不像有人建議的那樣[1,第260頁],模式看起來不平衡。相反,這與最初的凱爾特圖案是有限的設計,沒有散線頭有關。在一排圖案的末端,線條配對并連接配接在一起——這個過程需要偶數根線條。線條的數量與飾帶的寬度有關:寬度的奇偶性等于線條的數量的奇偶性。凱爾特人隻能在確定連續性的情況下使用奇數寬度的飾帶,例如在完整的邊界中。在一些地方,松散的結局自然發生。這些通常出現在動物形态中:奇怪的生物,它們細長的尾巴、四肢、脖子或舌頭以奇特的方式纏繞在一起。然而,這些圖案永遠不會大到有重複的圖案,是以不會提供飾帶的例子。
連續性、傳遞性和可分性
交錯圖案的設計者面臨的一個問題是如何确定完成的設計中的部件數量。在早期的凱爾特裝飾形式中,很明顯是在尋求路徑的連續性。作為永恒的象征,這一點很重要。即使是極其複雜的圖案,也隻有一根線條在無盡的回環中排列。在一些例子中,圖案的規則性被刻意放棄,圖案被修改,以確定獲得一條獨特的路徑。在後來的時代,這一規則被遵守得不那麼嚴格,但圖案中的回環仍然被避免了。這就提出了一個問題:是否有一種簡單的方法可以從斷裂标志的基本模式中确定設計中的條帶數。
當交織是編織的矩形部分時(圖14),那麼答案可以用邊界矩形來表示。如果辮子下面的晶格包含n×Rn單元,則圖案将具有單個分量,如果h.c.f。(m,n)~2.如果圖案為正方形(n=m),則分量數為[1/2n]。事實上,如果我們計算閉環而不是元件,那麼數字I/2n就可以被認為是正确的。當添加了斷點标記并拆分編織時,這些規則将不再有效。什麼規則取代了他們?
圖14:矩形圖案中的元件數量可以根據矩形的尺寸确定嗎?
交錯的飾帶怎麼樣:它們有多少條線?圖8f中的圖案是由無限多的封閉回環組成的鍊。圖8中的所有其他飾帶都有有限數量的無限長的條帶。大多數來自凱爾特人的圖案都有偶數條線;隻有非标準圖案a和b,以及我在圖8中設計的l、m和n有一條線;圖8d有三條線。
對于具有多個分量的圖案,我們可以研究對稱群是否對條帶起傳遞作用:每個條帶都可以通過圖案的某種對稱性被帶到任何其他條帶上嗎?在分層圖案和織物的背景中,線傳遞的圖案稱為等線圖案。采用這個術語,我們可以說,在圖8中的模式中,c和e不是等價式的,通過平移,除i和j之外的所有其他模式都是等價式的。在情況i和j中,需要旋轉才能實作完全的傳遞性。
有一個簡單的測試來檢查交錯的飾帶圖案是否相等。通過将飾帶的基本區域的兩端連接配接在一起來構造商連結。如果這個商鍊隻有一個分量,那麼平移後的飾帶是等價的。
在對織物的數學研究中出現的另一個問題是,确定一個分層的圖案是否會散開:這些線是否可以分成兩組或多組不相連的線?上面我們假設飾帶是相連的。這樣做的一個後果是凱爾特的交錯飾帶永遠不會散開。如果一條交錯的飾帶是交替的、連接配接的和可分離的,那麼由它構成的商鍊也是如此。然而,當且僅當連結沒有連接配接時,連結的交替圖表示分離連結[4]。
更精細的分類
在某些時候,将衆多的凱爾特交錯圖案分為10類是不太令人滿意的,特别是當我們意識到所産生的三維對稱類型完全是由底層的二維斷裂标志圖案決定的。如果能按圖案類型[3]而不是僅僅按對稱性類型進行某種分類就更好了。
直覺地說,圖案是以系統方式排列的圖案的集合。這種規律性在數學上是通過要求圖案的對稱群對圖案的過境作用來模拟的。按圖案類型分類取決于三個因素:圖案的對稱群G;圖案M的穩定器stabG(M);以及G的圖案傳遞性子群集合。
然而,當我們試圖将這種分析應用于凱爾特飾帶時,我們立即遇到了困難:圖案不是離散的,是以沒有明顯或自然的方法将它們分成圖案。字元串的連續性使得不可能以明确的方式選擇圖案,所做的選擇将影響最終的圖案類型。具有諷刺意味的是,與交錯的飾帶圖案相關的斷裂标記的排列是離散的,但不一定是過渡的。
尾聲
在這篇關于凱爾特結的研究中,我專注于一個特别的主題:對稱性。對稱性方面的分析是可能的,部分原因是設計結構背後的格子結構。這種内在的規律性和藝術家強加的周期性意味着許多圖案具有不平凡的對稱性。讀者可能會覺得,同樣的僵化會導緻一種枯燥乏味的藝術形式。一位面對根據對稱類型對圖案進行數學分類的非數學家寫道[2,p.70],
不存在圖案制作者的資源被幾何圖形的限制耗盡的危險。
在這種情況下,這句話似乎也是合适的。看一眼凱爾特人的手稿,你會很容易地相信幾何架構絲毫不妨礙藝術家的創作。想象力和創造力仍然有表達自己的空間。
參考文獻
1. J. Romilly Allen,Celtic Art in Pagan and Christian Times,London: Methuen (1904).
2. E. H. Gombrich,The Sense of Order: a study in the psychology of decorative art,Ithaca, NY: Cornell University Press (1979).
3. B. Gr~nbaum and G. C. Shephard,Tilings and Patterns,New York: Freeman (1987).
4. W. W. Menasco, Closed incompressible surfaces in alternating knot and link complements.Topology23 (1984), 37-44.
5. A. V. Shubnikov and V. A. Koptsik,Symmetry in Science and Art(translated from the Russian by G. D. Archard), New York: Plenum (1974).