考研數學函數極限的存在定理海涅定理（歸結原則）

海涅定理是用來證明函數極限存在的一個充分必要條件，它是根據數列極限存在與函數極限的關系發展而來

海涅定理：設f在u°(x。；)上有定義，則存在的充要條件為：對任何含于

u°(x。；)且以x。為極限的數列{}，極限都存在且相等。

接下來我們一起分析一下這個定理。

假設函數f的圖形如圖所示

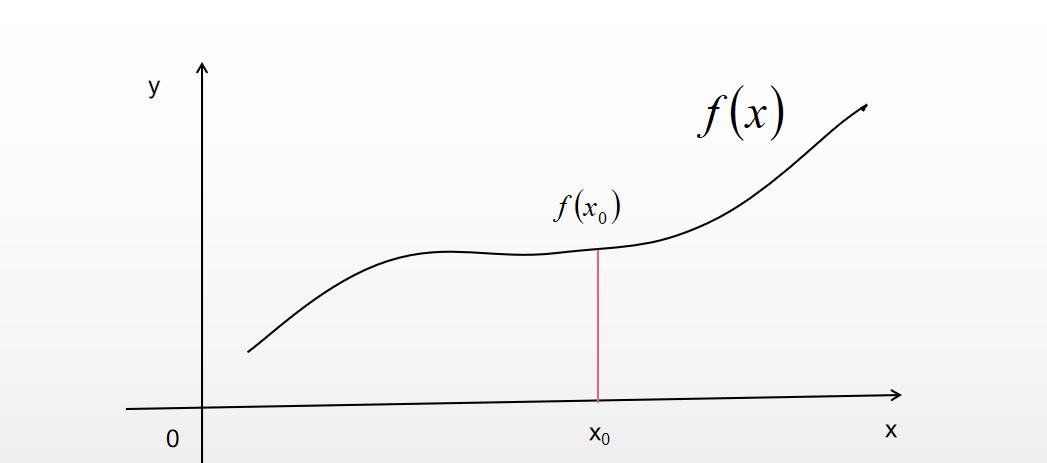
函數圖像

在點的周圍我們可以找到無窮多個數列,,……而且這些數列都以為極限。因為在實數軸上，實數軸上的每一點都代表一個實數，每個實數周圍都密密麻麻分布着無窮多個實數，而這些實數可以組成無限多個以為極限的數列。

當n∞時，有

f()f( )

……

是以，對任何含于u°(x。；)且以x。為極限的數列{}，極限都存在且相等。

這也就意味着存在。

最後我們根據上面的分析來證明一下這個定理。

證：首先我們來證明定理的必要性，我們現在已經知道存在

設=A，則

根據函數極限的定義可得 對＞0，＞0，當0＜＜時，有

＜ε

于是在（）内會存在無窮多個以為極限的數列（數列極限的緻密性定理）

最後我們來證明這個定理的充分性，我們用反證法。

假設≠A，則

根據函數極限的定義，有

＞0 ，對δ＞0，當0＜ ＜δ時，有

≥

現在我們取＜δ

令=、＝、、……、，則

數列的極限為，再根據的任意性

進而對于任意一個以為極限的數列，有≠A

這與已知條件“對任何含于u°(x。；)且以x。為極限的數列{}，極限都存在且相等。”相沖突。

是以，存在