(機率密度函數可以完整的表述随機變量和随機過程的統計特性)
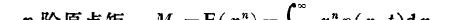
當n=1時表示均值,n=2時表示均方
當n=2時表示方差,
注意:信号的直流分量指的是信号的均值
參考:https://blog.csdn.net/wordwarwordwar/article/details/63251674
如下為常見的:
均值
連續,随機過程,表示t時刻所有樣本的總體均值
表示單樣本所有時刻的均值
當信号是各态周遊時相等。
性質:
方差
方差性質:
相關函數
自相關函數
确定信号下:
随機信号:
平穩過程:
和t無關
信号各态周遊:
上述公式等于單樣本的自相關函數
性質:
1)對稱性R(x)=R(-x)
功率譜密度函數(稱功率譜)
自相關和功率譜是一對傅氏變換
功率譜和能量譜的差別https://blog.csdn.net/wordwarwordwar/article/details/52695415
https://zhuanlan.zhihu.com/p/40481049
功率信号和能量信号的差別,這篇文章還不錯:
https://zhuanlan.zhihu.com/p/35363670
參考:[1]機率論與數理統計
[2]生物醫學信号處理
對數字特征的講解不錯:https://blog.csdn.net/TheSnowBoy_2/article/details/69564226
統計和機率的差別?
統計是,依據過去的資料總結歸納出總體(由樣本到總體)
機率是,總體資料對樣本進行預測(給定條件由總體到樣本)
https://www.zhihu.com/question/20269390