Yang Hui Triangle:
Yang Hui triangle, also known as Jia Xian triangle or Pascal triangle, is a geometric arrangement of binomial coefficients in triangles, using triangles to explain in detail the square law of binomial sum, appearing in the book "Detailed Explanation of the Nine Chapters Algorithm" written by the Chinese Southern Song Dynasty mathematician Yang Hui in 1261. In Europe, Pascal (1623----1662) discovered this law in 1654, so this table is also called Pascal's Triangle. Pascal's discovery was 393 years later than Yang Hui's, a great achievement in the history of Chinese mathematics.
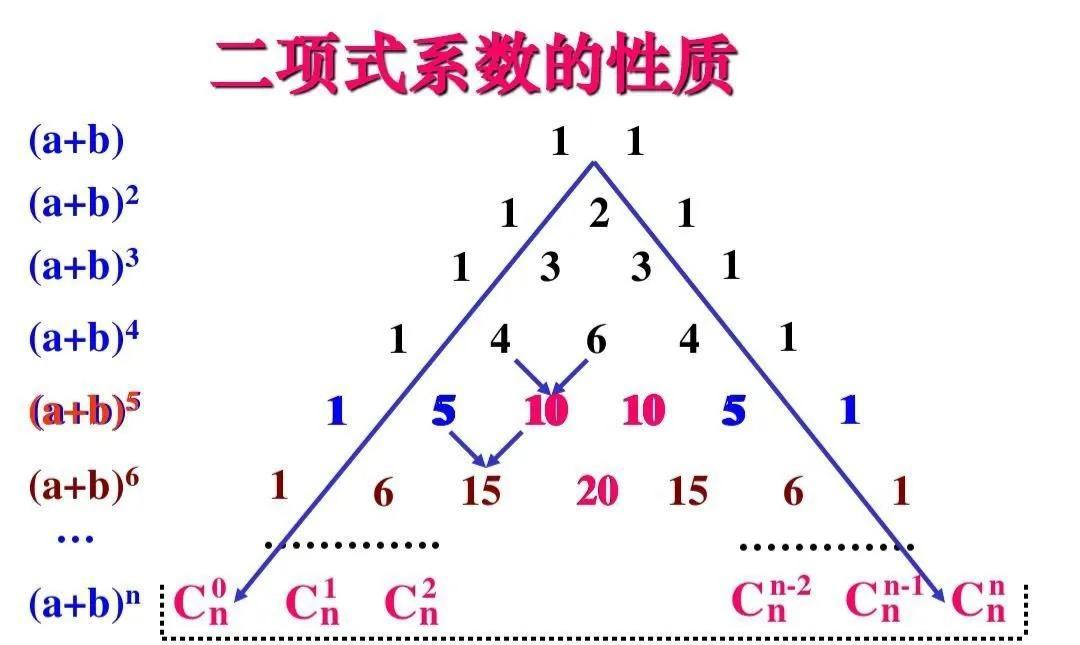
We find from this schematic diagram of the Yang Hui triangle that the number at the beginning of each line and the end of each row in the Yang Hui triangle is 1. Moreover, each number is equal to the sum of its upper left and upper right numbers, that is, 4 + 6 = 10, 5 + 10 = 15 in the figure. In this way, we found that Yang Hui's triangle is symmetrical left and right, and each expanded coefficient can be directly seen, which provides a convenient calculation method for our future mathematical learning, and can write out all terms through the law.