The core of artificial intelligence is machine learning, and in recent years, a new star has emerged in the field of machine learning, gan (Generative Adversarial Networks), proposed by Goodfellow et al. in 2014, and there are currently a large number of application examples in image identification and video generation. The basic idea of GAN derives from the zero-sum game of game theory, in which participants consist of a generator G (Generator) and a discriminator D (Discriminator), which are trained through the method of adversarial learning. The purpose of G is to try to learn the data distribution of the real data set R, while the purpose of D is to try to correctly determine whether the input data is from R or G. In order to win the game, the two game participants need to constantly optimize their strategies, improve their generative ability and judgment ability, and the whole learning optimization process is to find a Nash equilibrium between the two.
However, like other machine learning algorithms, the biggest problem facing GANs is the so-called "dimensional disaster", that is, the number of training sets required for learning increases exponentially with the dimensionality. If the data we are facing exists in high-dimensional space, then classical computers will soon be unable to process it efficiently. Fortunately, we have a new way of computing dominated by the laws of quantum mechanics, that is, quantum computing, which can solve many problems that classical computers cannot solve or are too complex. A clear application is that quantum computers can use Shor's quantum algorithm to crack the RSA public key cryptography commonly used in the Internet and financial systems today. In terms of practicality, quantum search algorithms can be expected to be applied to big data retrieval; quantum annealing algorithms can be applied to optimization problems, such as logistics and transportation optimization; quantum simulations can be applied to quantum multibody physics and quantum chemistry research, such as biosynthesis and drug screening. Compared with other systems, the technical route of superconducting quantum computing has a dominant position in the direction of practical quantum computing.
So, can we combine GANs with quantum computing to design a more efficient Quantum Generative Adversarial Networks algorithm? This concept was first proposed by Dallaire-Demers et al., and its basic principle is similar to THAT, except that G and D are composed of quantum circuits or quantum networks, and the training dataset can also be quantum data (such as quantum states, etc.). So far, the demonstration of QGAN in the superconducting quantum computing platform is limited to the learning of single-bit quantum states, and its gradient calculation is still a classical differential method, so that the calculation accuracy is affected by the inherent differential error, which in turn affects the convergence of the final training. At the same time, quantum entanglement, which embodies quantum properties and serves as an important resource for achieving quantum hegemony, has not been reflected in existing studies.
Recently, fan juan, Xu Kai and Zheng Dongning research groups of the Institute of Physics of the Chinese Academy of Sciences/Beijing National Research Center for Condensed Matter Physics, together with the research groups of Tian Jianguo and Liu Zhibo of Nankai University, the Wang Haohua research group of Zhejiang University and the Deng Dongling research group of Tsinghua University, for the first time, the QGAN algorithm was promoted to more bit categories and multibody entanglement was introduced, and for the first time, the QGAN training guided by quantum gradient was realized in the superconducting quantum computing platform.
The experiment uses a quantum chip with an all-connected architecture containing 20 qubits, on which some high-level work including 20-bit Schrödinger cat state preparation and simulation of dynamic phase transitions has been achieved. This experiment uses 5 of these qubits, the corresponding quantum algorithm as shown in Figure 1, including multiple single-bit quantum gates, multiple multi-bit entanglement gates and multiple two-bit control gates, with a line depth of more than 20, the experiment needs to be guided according to the quantum gradient to continuously optimize the single-bit quantum gate parameters. To test the feasibility of the quantum gradient, the researchers first tried to train an arbitrary single-bit mixed state, and after about 140 steps of training, the resulting quantum state has a fidelity of 0.999 relative to the real situation, see Figure 2. On that basis, they changed the learning objective to a more complex two-bit specific or gate, and through about 190 steps of training, the researchers reproduced the truth table of the xenoor gate with a fidelity of 0.927, see Figure 3. This shows that QGAN has a lot of potential for learning complex quantum processes, and as systems grow in size, it can be directly extended to areas such as optimized control and self-guided quantum tomography.
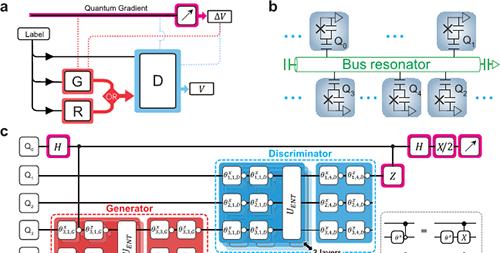
Figure 1. (a) QGAN flowchart. (b) A simple schematic diagram of the all-China Unicom sample chip. (c) QGAN actual algorithm circuit diagram, where the magenta part is a quantum gradient calculation circuit.
Figure 2. (a) The result of any single qubit mixed-state training. (b) The comparison of the trained and the true density matrix, which can reach 0.999 fidelity.
Figure 3. (a) Xor gate training results. The truth table fidelity of the training is 0.927. (b) Changes in the parameters of two characteristic single-bit quantum gates during training.
This work was recently published in NPJ Quantum Information 7, 165 (2021), and Nankai University co-trained phD student Huang Kaixuan, Q03 group phD student Wang Zheng'an, and Zhejiang University Distinguished Professor Song Chao as co-first authors of the paper. The cooperation team also includes Li Hekang, a postdoctoral fellow at Zhejiang University (preparer of a quantum chip), Wang Zhen, a distinguished professor at Zhejiang University, Guo Qiujiang, a researcher at The Hangzhou International Science and Technology Innovation Center of Zhejiang University, and Song Zixuan, a master's student at Zhejiang University.
In addition, Xu Kai, Associate Researcher, Fan Juan, and Zheng Dongning, Institute of Physics, Chinese Academy of Sciences, cooperated with professor Zheng Shibiao and Professor Yang Zhenbiao of Fuzhou University to achieve non-Abelian geometric controlled non-gates using two superconducting qubits and their auxiliary energy levels, and the relevant results were published in Optica 8, 972 (2021).
In cooperation with Professor Zhu Xiaobo and Professor Pan Jianwei of the University of Science and Technology of China, Fan Juan, a researcher and doctoral student at the Institute of Physics of the Chinese Academy of Sciences, using 12 superconducting qubits arranged in one dimension, experimental observations of different phenomena of heating intensity were realized by preparing different initial states corresponding to different temperatures. Rev. Lett. 127, 020602 (2021)。
bibliography:
[1] Kaixuan Huang#, Zheng-An Wang#, Chao Song#, Kai Xu, Hekang Li, Zhen Wang, Qiujiang Guo, Zixuan Song, Zhi-Bo Liu*, Dongning Zheng, Dong-Ling Deng*, H. Wang, Jian-Guo Tian, Heng Fan*, Quantum generative adversarial networks with multiple superconducting qubits, npj Quantum Information 7, 165 (2021).
[2] Kai Xu, Wen Ning, Xin-Jie Huang, Pie-Rong Han, Hekang Li, Zhen-Biao Yang*, Dongning Zheng, Heng Fan*, Shi-Biao Zheng*, Demonstration of a non-Abelian geometric controlled-NOT gate in a superconducting circuit, Optica 8, 972-976 (2021).
[3] Fusheng Chen#, Zheng-Hang Sun#, Ming Gong#, Qingling Zhu, Yu-Ran Zhang, Yulin Wu, Yangsen Ye, Chen Zha, Shaowei Li, Shaojun Guo, Haoran Qian, He-Liang Huang, Jiale Yu, Hui Deng, Hao Rong, Jin Lin, Yu Xu, Lihua Sun, Cheng Guo, Na Li, Futian Liang, Cheng-Zhi Peng, Heng Fan*, Xiaobo Zhu*, Jian-Wei Pan, Observation of strong and weak thermalization in a superconducting quantum processor, Phys. Rev. Lett. 127, 020602 (2021).
EDIT: just_iu