曹沖生五六歲,智意所及,有若成人。時孫權嘗緻巨象,太祖欲知其斤重,訪之群下,鹹莫能出其理。沖曰:“置象于船上,而刻其水痕所至,稱物以載之,則校可知矣。複稱他物,則象重可知也”太祖悅,即施行焉。
上面這段文字你是否覺得很熟悉?
那時候的你學完這堂課後你學會了什麼?
是否跟我一樣隻知道那時候的曹沖相對來說比較聰明。而沒有去研究稱象的這個方法所包含更深層的意義。最近忙完了一些事情,閑了下來。某天突然間想起這則故事,就多想了一下稱大象的過程感覺還挺有趣的,接下來我們一起稱大象吧。
把大象稱一下需要幾步?
按照原文的步驟,第一步,置象于船上,而刻其水痕所至。把大象趕到船上,然後沿着水面在船體标記大象在船上時船體下沉的深度。
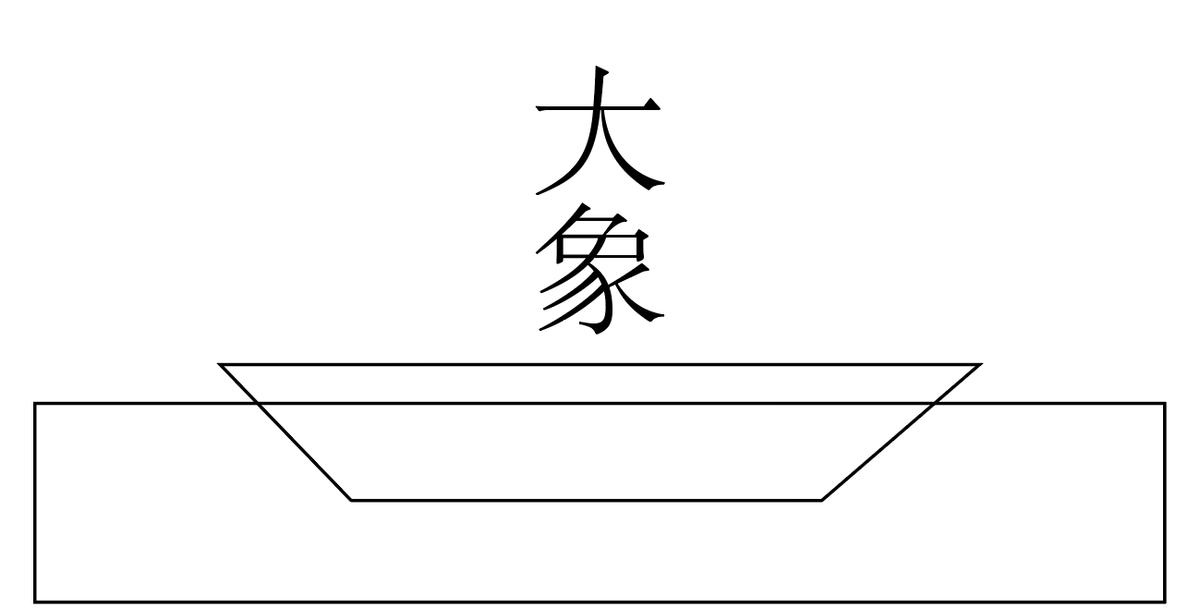
第二步,稱物以載之,則校可知矣。把大象趕上岸後往船上裝石頭,使船體下沉到标注的位置。
第三步,複稱他物,則象重可知也。使用稱稱出石頭的重量,就知道大象的總量。
為什麼稱石頭可以知道大象的重量。
答案是因為有船作為天平,大象在船上時下沉的深度等于石頭下沉的深度,是以大象的重量=石頭的重量。至此,大象的重量就稱出來了。
如果孫權送給曹操的不是一頭大象而是很多頭大象,要知道每一頭大象的體重你覺得該如何去稱出一群大象的體重?要搬多少次石頭?
在把大象趕上船之前先沿着水面在船體做标記設為标記一(這裡可以叫做清零)。把大象趕上船後沿着水面在船體做标記設為标記二。把大象趕下去後就得到下圖船體标記線。
假設稱完石頭後石頭的總重量為1000kg,用尺量出标記一到标記二的垂直高度為30cm。假設船體比較垂直的話船體的下沉深度和船上重物為線性關系,船體從标記一處開始下沉下沉深度為30cm船上的重物就是1000kg。理想狀态下沉深度為15cm時船上的重物就是500kg。有如下表格資料:
以實際重量為y軸,船體下沉深度為x軸繪制圖表。設定趨勢線,顯示線性公式,所得線性公式為:y=33.333x。
把剩餘的幾頭大象分别趕到船上标記船體下沉深度。根據之前計算獲得的線性關系(y=33.33x,x船體下沉深度)把船體下沉深度代入線性關系即可計算出剩餘幾頭大象的實際重量。這樣的話就隻需要搬一次石頭即可計算出其餘大象的總量。
實際稱象存在着較大的偏差,也沒有理想的線性下沉關系。因為船體一般都是弧形的,是以下沉關系并非直線線性關系,也許是曲線。船體形狀可能是這樣的。
那麼船體下沉的關系資料,假設。
根據圖表資料可知使用簡單的線性關系式所計算的趨勢線拟合度比較差。最終如果使用該關系式進行稱象難免會存在缺斤少兩的情況存在。
那如何增加準确性呢?
把線性改為多項式關系式。
根據圖中顯示所知趨勢線與實際幾乎重合,r平方值從0.9675上升到0.9998,非常接近實際資料。
如果使用該方法稱象首先用已知重量的石頭按照一定比例添加到船上标記船體下沉深度記錄船體下沉與重量的關系。然後計算出關系式,把大象趕到船上記錄船體下沉深度,把船體下沉深度代入關系式計算出大象的重量。
你知道電子秤稱重的原理嗎?
你知道傳感器的溫度補償是什麼原理嗎?
你知道為什麼可以通過氣體壓力傳感器可以測量到氣體的流速和容積?