1.github項目位址
https://github.com/easylliu/gitlearning/tree/master/Sudoku
2.開發時間
| PSP2.1 | Personal Software Process Stages | 預估耗時(分鐘) | 實際耗時(分鐘) |
|---|---|---|---|
| Planning | 計劃 | 30 | 50 |
| Estimate | 估計這個任務需要多少時間 | 10 | 15 |
| Development | 開發 | ||
| Analysis | 需求分析 (包括學習新技術) | 120 | 180 |
| Design Spec | 生成設計文檔 | 無 | |
| Design Review | 設計複審 (和同僚稽核設計文檔) | ||
| Coding Standard | 代碼規範 (為目前的開發制定合适的規範) | ||
| Design | 具體設計 | 60 | |
| Coding | 具體編碼 | 240 | |
| Code Review | 代碼複審 | ||
| Test | 測試(自我測試,修改代碼,送出修改) | ||
| Reporting | 報告 | ||
| Test Report | 測試報告 | ||
| Size Measurement | 計算工作量 | 20 | |
| Postmortem & Process Improvement Plan | 事後總結, 并提出過程改進計劃 | ||
| 合計 | 560 | 975 |
3.解題思路描述
(1).數獨終局生成
開始在看到題目時想到的是通過初始點一直往後延伸推導,後來想了一會感覺有點複雜;在思考無果後通過上網查找資料了解到生成終局的兩種方法
随機法,矩陣轉換法;但相比之下感覺矩陣轉換法更加直接,随機法不确定性加大了難度;而由于第一個數已經确定為9,是以第一行第一列不能參與變換,這樣通過一個數獨變換能産生共計5184種;但我們的要求最多有1000000種,是以想産生200個種子數獨,從8個數中取出四位,共有70種取法,而每種取法又對應三種數字交換方式共計210種符合要求,這樣産生的數獨數就已經超過1000000種符合要求了。
(2).求解數獨
在求解數獨上,開始自己思考是想通過那些已确定的那些數字出發,沿着他們所在行列塊進行推導,但随後感覺有點困難;通過網上查找感覺方法差不多,相對較為直接的就是回溯法求解了,從最開始點一直遞歸周遊找到所有存在的可能性,在通過行列和3*3塊的驗證來确定是否符合條件,簡單粗暴,在實作上較為簡單,初始計劃打算就使用了這種方法。
4.設計實作過程
(1).數獨終局生成
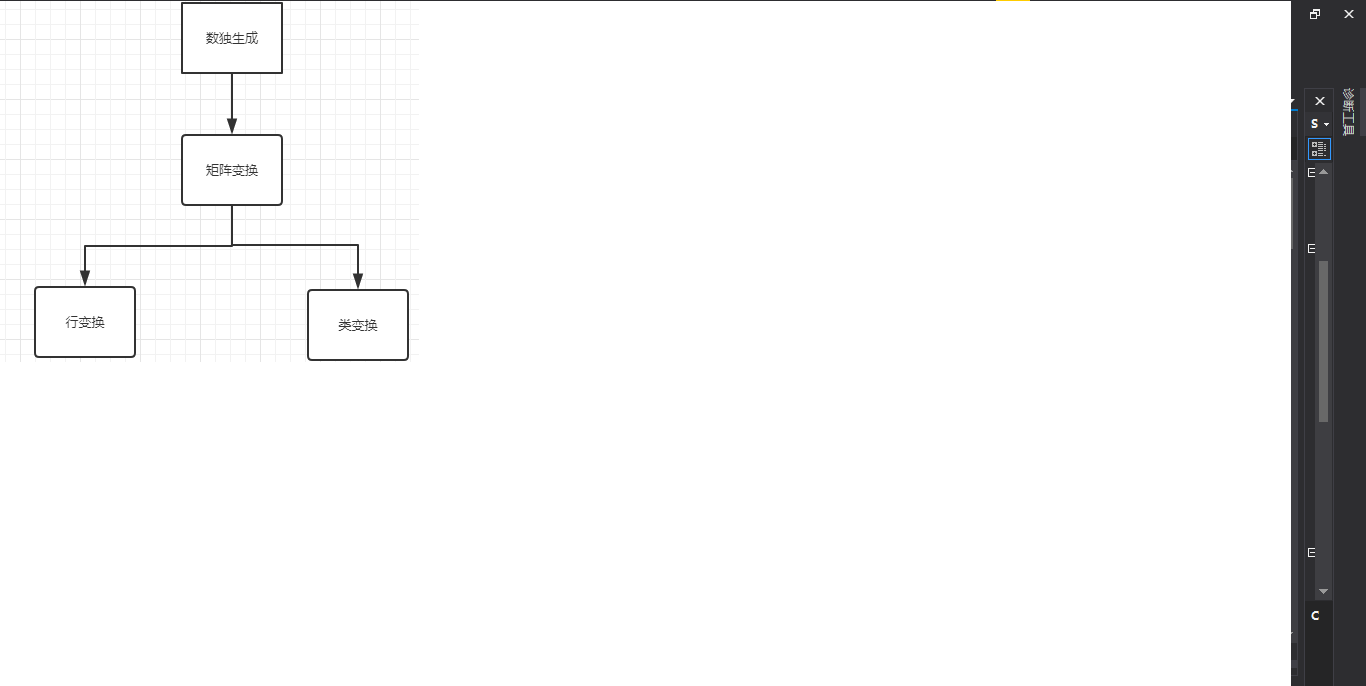
根據思路想到,首先産生的一個種子出發,首先通過其行列變換最多産生5184個數獨,如果還不足的話從那70種取法中随機選出先交換數字産生新的種子數獨,然後再行列變換,如此種種,在一定程度上還可以保證随機性,直到産生夠所要的數獨數即可結束。通過這種思路建構函數也就清晰起來,在數獨産生的函數中通過種子數獨不斷調用矩陣變換函數,然後可将矩陣變換函數拆解成行變換函數和列變換函數,如此這樣,函數之間的聯系清晰明朗,實作起來目标也很明确。總得來說在這一部分産生4個函數,其直接的關系也是層層調用。通過這樣的分析對函數的作用了解也清晰許多,通過他們直接的聯系和他們的用途設計單元測試就比較輕松了。
(2).求解數獨
通過暴力解法,對從0到81的所有空白進行1到9的選擇,然後判斷适合符合行列和塊的要求,然後遞歸往下延伸,當後面推不出來遞歸傳回繼續延伸推導,直到求解出正确的結果結束。
相對來說這種接法也相對較為直接,從0到81,先填入數字,在判斷是否符合行列和塊的要求,然後遞歸向後延伸。如此這樣分析,相對複雜點的就是遞歸的使用,想都來說3個函數足以。主函數調用填空遞歸函數,遞歸函數在填入數字後調用檢查函數判斷是否符合行列塊的要求,如此實作。然後相對來說,對遞歸的單元測試也相對有些麻煩,通過從對函數功能的了解出發,結合和其他函數的聯系設計單元測試會更加全面。
5.性能改進
改進:由于産生數獨和求解數獨的最大值已到達1000000,在輸出到檔案和讀取時的效率問題就顯得尤為重要了,是以在這方面花費時間能減就減,是以我就從每次寫入到檔案的數量上做出了改進,再往檔案裡寫入數獨時,我改進到每次寫入兩百個數獨,這樣減少寫入的次數,提高效率。
由圖檔中可以看到,調用次數最多的為檢查行列塊的合理性函數,這也是暴力求解産生的負面效果,其次在面對檔案操作時話費的時間較多,仍待改善。
6.代碼說明
主要分做兩個部分,一個是産生終局數獨,一個是求解數獨。
這四個為生成終局數獨的四個關鍵函數:
主要就是sudo_create産生種數獨通過調用矩陣變換得到擴充的數獨,矩陣變換由行變換和列變換組成;
void sudo_create(int sudo_count, char sudo[9][10], char changenum_array[70][5]); //生成數獨
int matrix_change(int count, int sudo_count, char sudo[9][10], char output[1000000]); //矩陣變換
void line_range(int init, int n, char mid_sudo[9][10], char sudo[9][10]); //行交換
void column_range(int init, int n, char mid_sudo[9][10], char sudo[9][10]); //列變換
其中最為關鍵一個:産生種子,調用擴充
void sudo_create(int sudo_count, char sudo[9][10], char changenum_array[70][5]) {
int index_changenum[70] = { 0 }; //是否随機到辨別符
char sudo_middle[9][10]; //中間種子數獨
int randnum = 0, i, j;
int count = 0; //已生成的數獨數
char a, b, c, d;
for (i = 0; i<9; i++) { //初始化
strcpy_s(sudo_middle[i], sudo[i]);
}
count = matrix_change(count, sudo_count, sudo_middle, output); //根據一個種子轉換輸出
while (count < sudo_count) {
if (count == -1) break;
randnum = rand() % 70 + 0;
if (index_changenum[randnum] == 0) { //未随機到
a = changenum_array[randnum][0];
b = changenum_array[randnum][1];
c = changenum_array[randnum][2];
d = changenum_array[randnum][3];
for (i = 0; i < 9; i++) {
for (j = 0; j < 9; j++) {
if (sudo[i][j] == a) {
sudo_middle[i][j] = b;
}
else if (sudo[i][j] == b) {
sudo_middle[i][j] = a;
}
else if (sudo[i][j] == c) {
sudo_middle[i][j] = d;
}
else if (sudo[i][j] == d) {
sudo_middle[i][j] = c;
}
else
sudo_middle[i][j] = sudo[i][j];
}
}
count = matrix_change(count, sudo_count, sudo_middle, output);
if (count == -1) break;
for (i = 0; i < 9; i++) {
for (j = 0; j < 9; j++) {
if (sudo[i][j] == a) {
sudo_middle[i][j] = c;
}
else if (sudo[i][j] == b) {
sudo_middle[i][j] = d;
}
else if (sudo[i][j] == c) {
sudo_middle[i][j] = a;
}
else if (sudo[i][j] == d) {
sudo_middle[i][j] = b;
}
else
sudo_middle[i][j] = sudo[i][j];
}
}
count = matrix_change(count, sudo_count, sudo_middle, output);
if (count == -1) break;
for (i = 0; i < 9; i++) {
for (j = 0; j < 9; j++) {
if (sudo[i][j] == a) {
sudo_middle[i][j] = d;
}
else if (sudo[i][j] == b) {
sudo_middle[i][j] = c;
}
else if (sudo[i][j] == c) {
sudo_middle[i][j] = b;
}
else if (sudo[i][j] == d) {
sudo_middle[i][j] = a;
}
else
sudo_middle[i][j] = sudo[i][j];
}
}
count = matrix_change(count, sudo_count, sudo_middle, output);
if (count == -1) break;
}
}
//cout << output;
}
這三個為求解數獨的主要函數:
主要就是solve_sudo函數調用填空進行遞歸,填入一個數後就判斷其合理性
int solve_sudo(char output[], int count);//求解數獨
bool solve_blank(int sudo_num);//填空
bool matrix_judge(int line, int column, int choose);//判斷合理性
關鍵一個函數:遞歸調用,逐漸展開
//填數
bool solve_blank(int sudo_num) {
int line, column, i;
line = sudo_num / 9;
column = sudo_num % 9;
if (sudo_num >= 81)
return true;
if (sudo1[line][column] == 0) {
for (i = 1; i <= 9; i++) {
sudo1[line][column] = i;
if (matrix_judge(line, column, i)) {
if (solve_blank(sudo_num + 1)) return true;
}
sudo1[line][column] = 0;
}
}
else {
return solve_blank(sudo_num + 1);
}
return false;
}