個人項目作業

軟體工程個人項目作業

1. 在文章開頭給出教學班級和可克隆的 Github 項目位址。

   項目	内容
   課程連結	2020春季計算機學院軟體工程(羅傑 任健)
   作業要求	個人項目作業
   教學班級	006
   項目位址	https://github.com/17373432/Project1

2. 解題思路描述。即剛開始拿到題目後，如何思考，如何找資料的過程。

   ​ 看到題目第一反應就是要按斜率将直線分類，假設有m組斜率，分别為\(k_1,k_2,...,k_m\)，每組斜率的直線分别有\(a_1,a_2,...,a_n\)個，最終答案即為\(\dfrac{\sum\limits_{i=1}^m (a_i×\sum\limits_{j=1,j≠i}^m a_j)}{2}\)。但是這麼做并沒有考慮公共點的情況，為了處理公共點問題，必須要把交點計算出來，而上述方法不涉及交點計算，是以隻好放棄。

   ​ 暴力計算交點的複雜度是\(O(n^2)\)，題目設定了運作時間限制，是以肯定不能使用暴力算法，我采取了如下兩種剪枝方法：

   • 平行直線不相交，依然可以按照上述思路，隻計算斜率不同的直線的交點。
   • 如果直線a與直線b相交于一個已知的公共點p，則可以不用計算點p上其他直線與直線a、直線b的交點。

   但即便這麼優化，最壞情況時間複雜度依然是\(O(n^2)\)，目前沒能想到更好的方法。

   ​ 關于找資料，我嘗試了在網上搜尋求直線交點個數問題的解法，但是都是不帶解析式不考慮三線共點的情況進行理論上最大值的求解，也有人理論分析并沒有快于\(O(n^2)\)的算法，是以并沒有什麼實際收獲。

3. 設計實作過程。設計包括代碼如何組織，比如會有幾個類，幾個函數，他們之間關系如何?
   • 主類：将各個類聯系起來，完成基本功能。
     • 屬性：map<斜率，set<對應斜率的直線>>，set<直線>，set<點>，set<圓>。
     • 方法：将直線按斜率儲存，以及求交點的一些方法。
   • Line類：采用一般式\(Ax+By+C=0\)，避免了斜率為正無窮的讨論。
     • 屬性：基本的A,B,C的值，以及其他簡化計算的屬性。
     • 方法：求與直線的交點，以及構造函數，傳回屬性的值，重載小于運算符等方法。
   • Point類：
     • 屬性：橫坐标x，縱坐标y，set<交于此點的直線>。
     • 方法：構造函數，傳回屬性的值，添加經過這個點的直線，重載小于運算符等方法。
   • Circle類：
     • 屬性：圓心(使用Point)，半徑，以及其他簡化計算的屬性。
     • 方法：求與直線的交點，求與圓的交點，以及構造函數，傳回屬性的值，重載小于運算符等方法。

   其他函數：浮點數相等比較(設定的浮點誤差為\(10^{-12}\))。

   關鍵函數是否需要畫出流程圖？

   ​ 這次由于沒畫流程圖，導緻複雜的函數如求直線與直線的交點的函數寫了很久。因為涉及的容器過多、循環層數多，每次查找的時候都得花很多時間來理清思路。

   單元測試是怎麼設計的？

   • 涉及了兩兩之間的每一種情況：直線與直線平行、相交，直線與圓相交、相切、相離，圓與圓内含、内切、相交、外切、相離。
   • 涉及了直線斜率為0，斜率不存在的情況。
   • 測試了浮點誤差可能導緻的相交視為平行的情況。
   • 進行了壓力測試(見test\*.txt檔案)。

4. 記錄在改程序式性能上所花費的時間，描述你改進的思路，并展示一張性能分析圖（由 VS 2019 的性能分析工具自動生成），并展示你程式中消耗最大的函數。

   這是1000個資料運作後的分析：

   

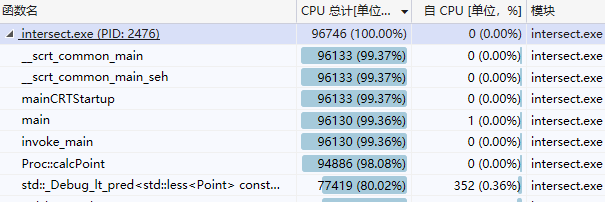
   其中的std::_Tree那一項是set和map的.insert()與.find()函數，花費了大量的時間，仔細分析代碼後發現我的容器全部使用的是set，在每次合并的時候都會比較是否與其他元素相同，是以每進行一次set的合并，這個元素與其他元素的比較就會多一次。改進方法即為隻将最外一層容器使用set，中間運算過程的容器使用vector，這樣保證每個元素到最後都隻會與其他元素比較一次。改進之後确實提升了一些性能。不過後來才發現運作時間這麼長其實是因為開的Debug模式進行分析，是以這張圖檔上的數字的意義其實不大，但是相對大小關系還是可以參考的。

   這是7000個資料運作後的分析：

   

   其中大部分時間仍然是set的.find()和.insert()，查找資料後得知c++中的map與set是用紅黑樹實作的，查找和插入的時間複雜度是\(O(logn)\)，是以我就找了時間複雜度為\(O(1)\)的unordered_set來代替set，同樣的7000個資料結果如下：

   

   可以看到，圖中std::_Hash這一項CPU總計比之前的std::_Tree少了接近40000，反應到最終的結果從1分30秒的執行時間減少到了35秒。果然資料多了之後\(O(logn)\)和\(O(1)\)算法的時間差異就展現了出來，可見容器的選擇十分重要。再附上具體代碼比較的圖：

   

   同一段代碼，上圖為使用set的具體代碼分析，下圖為使用unordered_set

   

5. 代碼說明。展示出項目關鍵代碼，并解釋思路與注釋說明。

   類圖：

   

   • 首先，最關鍵的還是浮點數相等比較，浮點數有誤差，計算中很難做到完全相等，是以要設定一個精度來進行等于判斷。

     #define eps 0.00000000001
     
     inline bool dEqual(double x, double y) {
     	double temp = 0;
     	bool result = false;
     	temp = abs(x - y);
     	if (temp < eps) {
     		result = true;
     	}
     	return result;
     }
                

     這裡的eps我設定的是\(10^{-12}\)，這個甯可多開幾位小數也不能少開，不然很可能在相切、平行這種地方出問題。
   • 直線預處理：将直線按斜率排序。

     void Proc::preProcLine(Line line) {
     	map<double, vector<Line>>::iterator iter;
     	iter = preMap.find(line.getK());
         // 如果存在斜率k,則加入k對應的直線組中
     	if (iter != preMap.end()) {
     		vector<Line> s = iter->second;
     		s.push_back(line);
     		preMap[line.getK()] = s;
     	}
         // 如果不存在斜率k,則建立一個鍵對
     	else {
     		vector<Line> s;
     		s.push_back(line);
     		preMap[line.getK()] = s;
     	}
     }
                

     這裡使用Map<double, vector<Line>>，做到從斜率映射到直線組，簡化後續計算。因為在之後的分析中發現這個Map的查找和插入執行總時間很短，是以并沒有将其改成unordered_map。
   • 計算兩條直線的交點

     Point Line::withLine(Line l) {
     	const double a2 = l.getA();
     	double b2 = l.getB();
     	double c2 = l.getC();
     	//a2*b!=a*b2
     	double deno = (a2 * b - a * b2);
     	double y = (a * c2 - a2 * c) / deno;
     	double x = (b2 * c - b * c2) / deno;
     	Point p(x, y);
     	return p;
     }
                

     套公式即可。注意這裡的deno是分母，不能等于0，是以要提前判斷

     a2*b!=a*b2

     ，即直線不平行，不過下面我已經保證了不會計算相同斜率的直線的交點，是以沒必要再進行判斷。(為了保持各個類之間的獨立性和代碼的穩定性，在這裡加一個出錯處理會更好，不過時間不是很充裕，是以沒有加)
   • 計算一個圓和一條直線的交點

     vector<Point> Circle::withLine(Line l) {
     	vector<Point> s;
     	const double x0 = o.getX();
     	const double y0 = o.getY();
     
     	const double delta = 
             r2 - pow(l.getA() * x0 + l.getB() * y0 + l.getC(), 2) / l.geta2Ab2();
     
     	if (delta >= 0) {
     		const double sqrtDelta = sqrt(delta);
     		const double leftX = 
                 (l.getb2() * x0 - l.getab() * y0 - l.getac()) / l.geta2Ab2();
     		const double rightX = sqrtDelta * l.getCos();
     		const double leftY = 
                 (l.geta2() * y0 - l.getab() * x0 - l.getbc()) / l.geta2Ab2();
     		const double rightY = sqrtDelta * l.getSin();
             // 注意rightX與rightY的符号不同
     		Point p1(leftX - rightX, leftY + rightY);
     		Point p2(leftX + rightX, leftY - rightY);
     		s.push_back(p1);
     		s.push_back(p2);
     	}
     
     	return s;
     }
                

     套公式即可。判别式delta大于0有2個交點；等于0有一個焦點；小于0無交點。注意算交點坐标時橫坐标和縱坐标右半部分符号是相反的(一開始就是這個地方的bug，不過很容易發現和修複)
   • 計算兩個圓的交點

     vector<Point> Circle::withCircle(Circle that) {
     	vector<Point> s;
     	const double max = r + that.r;
     	const double min = abs(r - that.r);
     	const double d = 
             sqrt(pow(o.getX() - that.o.getX(), 2) + pow(o.getY() - that.o.getY(), 2));
     
     	if (min <= d && d <= max) {
     		const double A = that.xx - xx;
     		const double B = that.yy - yy;
     		const double C = x2Ay2Sr2 - that.x2Ay2Sr2;
     		const Line l(A, B, C);
     		s = withLine(l);
     	}
     	return s;
     }
                

     套公式即可。這裡先求的是兩圓公共弦的表達式，然後利用公共弦再與任意一個圓相交求出交點。注意圓心距d要在大于等于兩圓半徑之差與小于等于半徑之和這個範圍中求出來的公共弦才有意義。(小于兩半徑之差求出來的是虛弦也可能與圓有交點導緻最終求出來交點變多)
   • 計算所有直線與直線産生的交點

     void Proc::lineAndLine() {
     	map<double, vector<Line>>::iterator iterM;
         // 周遊斜率k
     	for (iterM = preMap.begin(); iterM != preMap.end(); iterM++) {
     		vector<Line>::iterator iterS;
     		vector<Line> tempSet = iterM->second;
     		// 周遊斜率為k的直線
     		for (iterS = tempSet.begin(); iterS != tempSet.end(); iterS++) {
     			vector<Line>::iterator iterL;
     			Line l1 = *iterS;
     			set<int> inteId;
                 // 周遊已添加的直線
     			for (iterL = lineSet.begin(); iterL != lineSet.end(); iterL++) {
     				Line l2 = *iterL;
     				set<int>::iterator iterI = inteId.find(l2.getId());
                     // 如果l2與l1的交點已經被算出來了，就跳過
     				if (iterI != inteId.end()) {
     					continue;
     				}
     				Point p = l1.withLine(l2);
     				unordered_set<Point, hashPoint>::iterator 
                         iterP = pointSet.find(p);
     				// 如果這個點在點集中，就把在這個點上的其他直線的id加入inteId,減少計算
     				if (iterP != pointSet.end()) {
     					p = *iterP;
     					vector<int> temp = p.getLines();
     					inteId.insert(temp.begin(), temp.end());
                         // l1也在這個點上
     					p.addLine(l1.getId());
     				}
                     // 如果不在，就把l1,l2加入在這個點上的集合中,将這個點加入點集
     				else {
     					p.addLine(l1.getId());
     					p.addLine(l2.getId());
     					pointSet.insert(p);
     				}
     			}
     		}
             // 将斜率為k的直線全部加入已添加的集合
     		lineSet.insert(lineSet.end(), tempSet.begin(), tempSet.end());
     	}
     }
                

     l1為某個斜率下的某條直線，inteId為記錄l1已經和哪些直線相交(後續無需再計算l1和這些直線的交點)，儲存的是這些直線的交點，lineSet記錄的是已經周遊過的直線。

     具體過程：第一層循環，周遊各個斜率。第二層循環，周遊這個斜率的直線，記為l1，并用inteId記錄該直線與哪些直線已經相交。第三層循環，周遊之前已經周遊過的直線，記為l2，如果l2在inteId中則跳過計算，進行下一次循環；否則計算l1與l2的交點p。查找p是否已經出現過，如果已經出現過，則将p上的直線全部加入到inteId中，使得l1在後續碰到這些直線可以直接跳過不用計算，将l1計入交于p上的直線中；否則将l1和l2計入交于p上的直線中，将p加入最終的點集。在第二層循環結束後(即有一組k的直線已經被周遊完)，将這組直線全部加入lineSet中(這樣整體加入的好處是保證了相同斜率的直線不會進行計算)。

   • 計算所有直線與圓的交點

     void Proc::lineAndCircle(Circle circle) {
     	vector<Point> result;
     	map<double, vector<Line>>::iterator iterM;
         // 周遊斜率k
     	for (iterM = preMap.begin(); iterM != preMap.end(); iterM++) {
     		vector<Line>::iterator iterS;
     		vector<Line> tempSet = iterM->second;
     		// 周遊斜率為k的直線
     		for (iterS = tempSet.begin(); iterS != tempSet.end(); iterS++) {
     			Line l = *iterS;
     			vector<Point> s = circle.withLine(l);
     			vector<Point>::iterator iterS;
     			for (iterS = s.begin(); iterS != s.end(); iterS++) {
     				pointSet.insert(*iterS);
     			}
     		}
     	}
     }
                

     與計算所有直線和直線交點類似，外兩層循環周遊直線，記為l，然後求l與圓的交點。
   • 計算所有圓産生的交點

     void Proc::calcCircle() {
     	vector<Circle>::iterator iter1;
         // 周遊所有的圓
     	for (iter1 = circleSet.begin(); iter1 != circleSet.end(); iter1++) {
     		vector<Circle>::iterator iter2;
     		Circle circle1 = *iter1;
             // 計算該圓與所有直線的交點
     		lineAndCircle(circle1);
             // 計算該圓與已添加的圓的交點
     		for (iter2 = circleSet.begin(); iter2 != iter1; iter2++) {
     			Circle circle2 = *iter2;
     			vector<Point> s = circle1.withCircle(circle2);
     			vector<Point>::iterator iterS;
     			for (iterS = s.begin(); iterS != s.end(); iterS++) {
     				pointSet.insert(*iterS);
     			}
     		}
     	}
     }
                

     第一層循環，周遊每個圓，記為circle1，計算circle1與所有直線的交點。第二層循環，周遊已周遊過的圓，記為circle2，計算circle1與circle2的交點。
6. 代碼警告消除

   

7. 在你實作完程式之後，在下述 PSP 表格記錄下你在程式的各個子產品上實際花費的時間。

   PSP2.1	Personal Software Process Stages	預估耗時（分鐘）	實際耗時（分鐘）
   Planning	計劃
   · Estimate	· 估計這個任務需要多少時間	10
   Development	開發
   · Analysis	· 需求分析 (包括學習新技術)	120
   · Design Spec	· 生成設計文檔	30
   · Design Review	· 設計複審 (和同僚稽核設計文檔)
   · Coding Standard	· 代碼規範 (為目前的開發制定合适的規範)
   · Design	· 具體設計	60
   · Coding	· 具體編碼	360	300
   · Code Review	· 代碼複審		240
   · Test	· 測試（自我測試，修改代碼，送出修改）		420
   Reporting	報告
   · Test Report	· 測試報告
   · Size Measurement	· 計算工作量
   · Postmortem & Process Improvement Plan	· 事後總結, 并提出過程改進計劃
   合計	970	1270

   ​ 這次作業乍一看不是很難，是以具體設計、代碼複審、測試上的時間估算的比較少，越寫就越感覺自己程式設計能力不足，之前并沒有用c++寫過類，是以這次光是學習怎麼寫類、怎麼用unordered_set都花了很多時間，在測試方面研究為什麼性能降不下來，一直盯着代碼分析資料看，擺弄了好久才發現是分析報告裡面消耗最大的std::_Tree指的是紅黑樹，才有所進展。關于浮點精度取得不夠小導緻的最終結果少一個的bug也是找了好久才發現。

8. 個人總結

   ​ 一開始以為這次作業在計算上的時間開銷會比較大，是以拼命推公式化簡，盡可能多的找到可以預先存儲的值，拿空間換時間，但是寫了之後才發現，計算的時間隻是雞毛蒜皮，容器的查找和插入的時間就能占到95％以上，容器選的不好，做再多其他方面的優化也是白搭，相反容器選的好純暴力算法應該都能在規定時間内運作完。是以這次作業設立最大運作時間隻是為了讓我們意識到容器的重要性麼？

   ​ PS:這次作業時間真的是有點緊，周五才上完課把熱身部落格寫完，周六要寫其他作業，周一周二又有課，有效的工作時間就隻有周日和周一晚上，這次由于時間問題導緻很多地方都是草草了事，沒有加出錯處理，unorder_set也隻是瞎用，為了用這個容器還把Point類的屬性給public了，很多地方都沒按标準來。總之，我感覺這次的ddl對于我來說設定的太尴尬了，周二就隻有晚上有時間，周三一天沒有課，可截止日期偏偏是周二下午，這個時間對周五上課的同學來說太不友好了，由衷希望下次ddl能往後推一推。