個人項目作業

項目	内容
這個作業屬于哪個課程	2020春季計算機學院軟體工程(羅傑任健)
教學班級	005
項目位址	IntersectProject

PSP 表格記錄

PSP2.1	Personal Software Process Stages	預估耗時（分鐘）	實際耗時（分鐘）
Planning	計劃	15	30
· Estimate	· 估計這個任務需要多少時間	360-540	600
Development	開發	-
· Analysis	· 需求分析 (包括學習新技術)		60
· Design Spec	· 生成設計文檔	20
· Design Review	· 設計複審 (和同僚稽核設計文檔)
· Coding Standard	· 代碼規範 (為目前的開發制定合适的規範)	10
· Design	· 具體設計
· Coding	· 具體編碼	120	240
· Code Review	· 代碼複審
· Test	· 測試（自我測試，修改代碼，送出修改）		40
Reporting	報告
· Test Report	· 測試報告
· Size Measurement	· 計算工作量
· Postmortem & Process Improvement Plan	· 事後總結, 并提出過程改進計劃
合計	345	635

一開始對題目思考很不全面，會有某些情況未考慮到，或是手誤寫錯代碼導緻結果錯誤，實際耗時更多。

解題思路描述

題目要求求出交點個數，是以一開始想到的辦法偏重于個數。比如，兩條直線不平行必相交，會有一個交點；兩個圓，直線和圓的情況可能會産生0-2個交點。但是，這種沒考慮具體點的想法，會出現交點重合，重複計算個數的情況，是以還是需要考慮具體的交點坐标是多少。這樣就必須計算出坐标，分為三種情況：直線和直線，圓和圓，直線和圓。計算一條直線（圓）和其他所有直線（圓）的交點；計算每條直線和所有圓的交點。最終計算出的不重複的交點坐标的個數就是交點的個數。

上網查了一些關于直線相交，圓相交的資料，沒查到什麼太好的辦法，感覺都挺複雜的，自己也沒想到。于是推導出了直線與直線相交求交點的公式，其餘情況比較複雜，有如下參考：

兩圓相交求交點的參考

直線和圓相交的參考

這樣做複雜度應該會很高，但是目前沒有想到什麼更好的辦法。有過運用矩陣的想法，也許會降低一些運算量，但沒有想清楚應該怎樣使用，究竟能否使用也說不清，隻是感覺這種問題和矩陣有莫名的聯系。另外，N條直線相交最多産生 \(\frac{N(N-1)}{2}\) 個交點，這樣看好像本身複雜度也挺高的。但是，通過給的測試範圍能夠看出，一定存在很多交點重合的情況，如何才能減少不必要的運算而降低複雜度，性能問題仍然值得思考。

設計實作過程

首先，根據集合對象建立類，直線

Line

類及圓

Circle

類，同時應該有基礎機關點

Point

類。但是，根據

Point

類建立對象時，就算是兩個點坐标完全一樣，也會被認為是兩個對象，這和我的想法有些出入，并且開始寫時這個類也隻負責記錄某點的兩個坐标，于是删去（看了同學寫的部落格，感覺如果保留下來這個類，添加一些方法也是不錯的，比如計算一下兩點的距離，兩點構成直線的斜率和截距，可以讓代碼邏輯性更強，看起來也比較好看）。

對于直線類和圓類，需要相應的構造函數。直線需要計算出斜率k和截距b，圓根據輸入直接存為圓心坐标及半徑。在直線類中，應該有屬于直線與直線相交的計算函數；在圓類中，應該有圓與圓的計算函數；直線與圓相交的計算函數随便放進一個類（根據我的代碼放在圓類裡面比較友善）。

關于單元測試

首先是一些關于特殊資料的手寫樣例。如直線斜率不存在，為0，兩直線平行時；兩圓内切，外切，相離時；直線與圓相切，相交，相離時。這種資料可以通過在

GeoGebra

繪制并能大體看出結果。同時輸出直線的斜率和截距，交點坐标來檢查正确性。

另外是用大量的随機資料進行測試，專門寫了一個

intersect_test.cpp

進行測試。在構造直線和圓時随機生成了一些資料，後面的操作沒太大變化。

性能分析

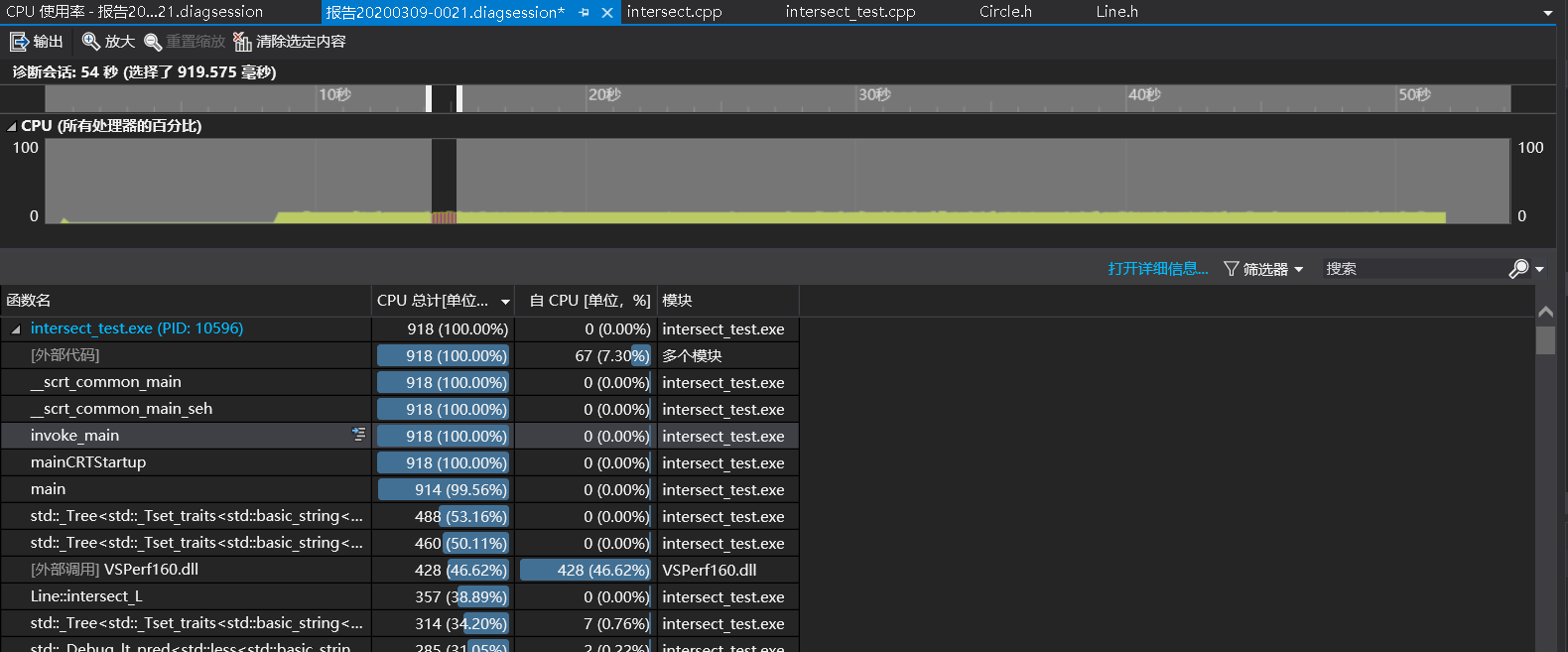
制造1000個随機資料，CPU使用如上圖，能看出來占比最多的基本是關于自帶的

Tree

和求交點的幾個函數，

Tree

應該與set容器的實作方式RBTree有關，求交點沒有辦法避免，但

to_string

函數也占比較多，這兩點也許可以改進。關于

to_string

函數，這一點目前來說是我認為比較必要的操作，考慮優化一下set容器。set容器是通過RBTree來實作有序，從CPU分析中也能看出來，但實際上我們不需要set有序，隻需要用它存儲一下已求出的交點坐标即可，查閱資料發現有一種

unordered_set

容器，更換後性能如下：

std::Tree

這個東西已經沒了，速度也比原先快了不少。現在主要是轉換字元串方法占比較多，還需要進一步考慮。

一點改進

用set容器存儲字元串雖然友善，但是

to_string

調用太多次太費時間，重拾遺棄的

Point

類，并且重載比較函數。需要注意的是，重載的比較函數主要就是多處理一下精度問題。否則會出現這種情況：

看起來是同一個點，其實在小數點後面十幾位之後是不同的，如果輸出的時候控制一下小數點位數是可以看出來的，但是直接輸出就會是上面這種情況。這樣改了以後1000個随機資料快了不少，分析如下：

主要問題還是RBTree的建構。如果堅持使用

unordered_set

容器，需要重寫Hash函數和等價準則，萬一寫錯了就會很麻煩，是以感覺還是選擇使用set。

代碼說明

最關鍵的代碼就是求交點的部分，如上所說，直線和直線相交比較容易推導出公式，涉及到圓的比較複雜。根據上面的參考得到如下代碼，首先是兩圓求交點部分：

void intersect_C(Circle otherCircle) {
		double center_d = sqrt((x - otherCircle.x) * (x - otherCircle.x)
			+ (y - otherCircle.y) * (y - otherCircle.y));
		if (center_d != 0) {
			double a = (r * r - otherCircle.r * otherCircle.r + center_d * center_d) / (2 * center_d);
			double x0 = x + a / center_d * (otherCircle.x - x);
			double y0 = y + a / center_d * (otherCircle.y - y);
			if ((center_d == r + otherCircle.r) || (center_d == abs(r - otherCircle.r))) {
				nodes.insert(to_string(trans(x0)) + "," + to_string(trans(y0)));
			}
			else if ((center_d > abs(r - otherCircle.r)) && (center_d < r + otherCircle.r)) {
				double h = sqrt(r * r - a * a);
				double x1 = x0 - h / center_d * (otherCircle.y - y);
				double y1 = y0 + h / center_d * (otherCircle.x - x);
				double x2 = x0 + h / center_d * (otherCircle.y - y);
				double y2 = y0 - h / center_d * (otherCircle.x - x);
				nodes.insert(to_string(trans(x1)) + "," + to_string(trans(y1)));
				nodes.insert(to_string(trans(x2)) + "," + to_string(trans(y2)));
			}
		}
	}

計算出圓心距，不為0時考慮内切，外切，相交的情況，把數學公式翻譯成代碼，思考起來比較容易，最後把計算出來的點加到set中。

然後是圓與直線求交點部分：

void intersect_L(Line line) {
		if (line.k == INFINITY) {
			double d = abs(line.b - x);
			if (d < r) {
				double offset = sqrt(r * r - d * d);
				double y1 = y + offset;
				double y2 = y - offset;
				nodes.insert(to_string(line.b) + "," + to_string(trans(y1)));
				nodes.insert(to_string(line.b) + "," + to_string(trans(y2)));
			}
			else if (d == r) {
				nodes.insert(to_string(line.b) + "," + to_string(y));
			}
		}
		else {
			double c = -x, d = -y, k = line.k, b = line.b;
			double delta = k * k * r * r + r * r - c * c * k * k + 2 * c * d * k +
				2 * b * c * k - d * d - 2 * b * d - b * b;
			if (delta > 0) {
				delta = sqrt(delta);
				double x1 = -((delta + k * d + k * b + c) / (k * k + 1));
				double y1 = -((k * delta + k * c + d * k * k - b) / (k * k + 1));
				double x2 = (delta - k * d - k * b - c) / (k * k + 1);
				double y2 = -((-k * delta + k * c + d * k * k - b) / (k * k + 1));
				nodes.insert(to_string(trans(x1)) + "," + to_string(trans(y1)));
				nodes.insert(to_string(trans(x2)) + "," + to_string(trans(y2)));
			}
			else if (delta == 0) {
				double x1 = (-k * d - k * b - c) / (k * k + 1);
				double y1 = (b - d * k * k - k * c) / (k * k + 1);
				nodes.insert(to_string(trans(x1)) + "," + to_string(trans(y1)));
			}
		}
	}

分為截距存在和不存在時的情況，同時考慮直線與圓相交，相切的情況，相離就直接略過。

其中有一個

trans

函數，由于

double

類型精度問題，字元串轉換後會出現

0.000000

和

-0.000000

的情況，實際上都是0，但會被認為是兩個點。根據資料限制，誤差應該不會超過 \(10^{-10}\) 或者再大幾個數量級。這一點在設計上确實存在缺陷。

由于能力不足，總體來看比較暴力，照貓畫虎按部就班······

Code Quality Analysis

如上圖，整體上沒什麼警告。有一點需要注意，起初警告說

size()

方法得到的是

size_t

類型的資料，轉換類型可能會造成資料丢失。百度了一下和平台有關，其實問題不是很大，為了好看前面加個強制類型轉換，具體可以看這篇部落格。