個人項目作業

項目	内容
作業所屬課程	2020春季計算機學院軟體工程（羅傑，任健）
作業要求
教學班級	005
項目位址	個人項目位址

PSP表格

PSP2.1	Personal Software Process Stages	預估耗時（分鐘）	實際耗時（分鐘）
Planning	計劃
· Estimate	· 估計這個任務需要多少時間	15	10
Development	開發
· Analysis	· 需求分析 (包括學習新技術)	60	120
· Design Spec	· 生成設計文檔		20
· Design Review	· 設計複審 (和同僚稽核設計文檔)
· Coding Standard	· 代碼規範 (為目前的開發制定合适的規範)
· Design	· 具體設計
· Coding	· 具體編碼	90	100
· Code Review	· 代碼複審		30
· Test	· 測試（自我測試，修改代碼，送出修改）
Reporting	報告
· Test Report	· 測試報告
· Size Measurement	· 計算工作量
· Postmortem & Process Improvement Plan	· 事後總結, 并提出過程改進計劃
合計	310	475

解題思路

對于給定的N條直線，詢問平面中有多少點在至少2條給定的直線上，即求出N條直線有多少不重複的交點。

首先我分析到輸入部分，每條直線對應線上不同的兩點，我首先根據這兩點計算得到直線的标準方程式，記得到三個重要參數:a, b, c：

ax + by + c = 0, a = y2 - y1, b = x1 - x2, c = y1x2 - x1y2;

同時我們保證a始終大于0。

得到每個直線的标準方程式後，我們就可以進行兩兩比較得到交點數了，若兩條直線的斜率不等，則說明兩條直線有交點，同時記錄交點的坐标資訊：

x = (b1c2 - c1b2)/(a1b2 - a2b1), y = (a2c1 - a1c2)/(a1b2 - a2b1);

在比對所有直線的相交情況後，我們就可以去掉計數了重複的點了，最後得到就是所有直線不重複的交點，即平面中至少在2條給點直線上的點數。

設計實作

程式中有四個函數，設計了兩個結構體：

直線标準式資訊（LINE）：

記錄了每條直線的a, b, c相應的值，采用double資料類型。

交點坐标資訊（Point2d）:

記錄每個交點的坐标軸資訊，包括x, y，采用double資料類型。

主函數（main）:

主要用于指令行的輸入輸出，首先對指令行進行處理得到所要的資料，将每個直線的兩點坐标資訊讀取傳遞給調用函數，傳回得到直線标準方程式資訊，然後調用計算交點數函數得到無重複的交點個數，傳回到輸出檔案中。

直線标準方程式函數（makeline）：

根據所給的直線兩點坐标，計算得到直線标準式a, b, c值，其中保證a值大于0,，傳回一個LINE資料結構體。

計算交點函數（calculateCrossPointsNum）:

周遊每條直線，檢視兩兩直線是否相交，統計并記錄交點坐标資訊，然後周遊交點資訊，取出重複的交點。

判斷直線是否相交函數（lineintersect）：

通過比較所給兩條直線的斜率，分析兩條直線是否平行，若直線相交計算并記錄交點的坐标資訊。

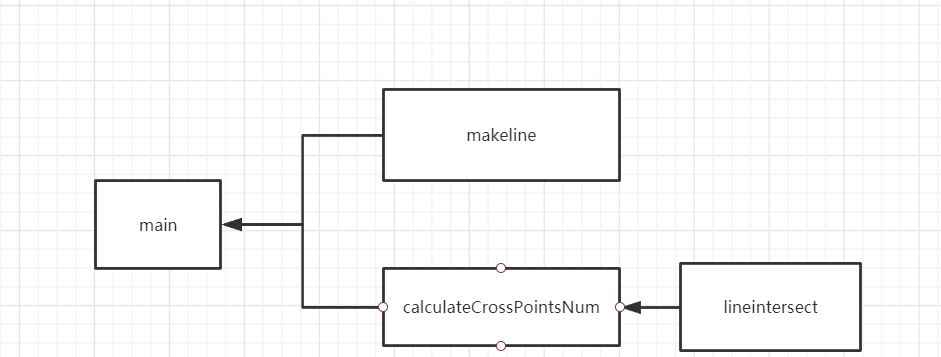
函數之間的關系：

主函數main通過調用makeline來根據點的坐标資訊得到直線的标準式資訊，然後通過calculateCrossPointsNum計算得到交點個數，calculateCrossPointsNum函數調用lineintersect來判斷兩兩直線是否相交：

單元測試主要根據樣例分析多種不同情況，考慮一條直線，多條直線相交一點，多條平行線等問題，均可實作。

性能分析表

性能分析圖（由 VS 2019 的性能分析工具自動生成）：

程式中消耗最大的是比較斜率過程。

代碼說明

通過指令行輸入直線資料：

int main(int argc, char* argv[])
{
	ifstream in;
	ofstream out;
	for (int i = 0; i < argc; i++) {
		if ((string)argv[i] == "-i") {
			in.open(argv[i + 1]);
		}
		else if ((string)argv[i] == "-o") {
			out.open(argv[i + 1]);
		}
	}

    int N; // 直線個數
	in >> N;

根據已知兩點坐标，求過這兩點的直線解析方程：a*x + b * y + c = 0:

LINE makeline(double x1,double y1,double x2,double y2)
{
    LINE tl;
    int sign = 1;
    tl.a = y2 - y1;
    if (tl.a < 0) {
        sign = -1;
        tl.a = sign * tl.a;
    }
    tl.b = sign * (x1 - x2);
    tl.c = sign * (y1 * x2 - x1 * y2);
    return tl;
}

如果兩條直線 l1(a1x+b1y+c1 = 0), l2(a2x+b2y+c2 = 0)相交，傳回true，且傳回交點p：

bool lineintersect(LINE l1, LINE l2, Point2d &p)
{
    double d = l1.a * l2.b - l2.a * l1.b;
    if (abs(d) < EP)
    {
        return false;
    }
    p.x = (l2.c * l1.b - l1.c * l2.b) / d;
    p.y = (l2.a * l1.c - l1.a * l2.c) / d;
    return true;
}

去掉重複點：

for (int i = 0; i < pnts.size() - 1; i++)
    {
        for (int j = i + 1; j < pnts.size(); j++)
        {
            if (pnts[i].x == pnts[j].x && pnts[i].y == pnts[j].y)
            {
                pnts.erase(pnts.begin() + j);
                j--;
            }
        }
    }

個人項目作業

個人項目作業

PSP表格

解題思路

設計實作

直線标準式資訊（LINE）：

交點坐标資訊（Point2d）:

主函數（main）:

直線标準方程式函數（makeline）：

計算交點函數（calculateCrossPointsNum）:

判斷直線是否相交函數（lineintersect）：

函數之間的關系：

性能分析表

代碼說明

Code Quality Analysis分析