個人項目-數獨
個人項目位址
https://github.com/ErisPluto/Sudoku
解題思路
- 需求分析
- 生成終局:
- 指令格式: sudoku.exe -c N
- 1 <= N <= 1000000
- 輸出到檔案: sudoku.txt
- 數獨不重複
- 數獨左上角第一個數為(學号後兩位相加)% 9 + 1 = (8 + 0) % 9 + 1 = 9
- 處理異常情況
- 求解數獨:
- 指令格式: sudoku.exe -s absolute_path_of_puzzlefile
- 數獨題目個數: 1 <= N <= 1000000
- 0代表空格,保證格式正确,對每個題目求出一個可行解
- GUI設計(可選): 如果能夠較好的完成前兩部分再來考慮GUI
- 生成終局:
- 相關思路
- 首先需要花一些時間來學習C++,熟悉github和visual studio
- 對于生成數獨終局,最先考慮到的是暴力回溯,逐個格從1-9周遊嘗試。由于生成數獨終局時左上角第一個格被限制,在回溯法的思路下,生成終局和求解數獨其實是一樣的。雖然肯定會慢,但是是一種明确的而且比較容易寫的方法,因為自身編碼能力不強,是以考慮到的就是先把功能實作再考慮性能的問題,是以決定使用回溯法,并沒有考慮去網上找一些更好的算法。
- 關于檔案的讀寫,最開始完全沒有意識到檔案讀寫花費的大量的時間,于是采用的是逐個讀逐個寫的方法。
設計實作
-
生成數獨/求解數獨
由于沒有去網上找其他算法,是以基本上是離不開回溯法的,盡管如此,由于側重點的不同還是前後改了三個版本
-
第一個版本非常希望能在不重複的基礎上增加随機性,根本沒有考慮性能的問題
在回溯法的思路下,希望能夠給生成的數獨終局一些随機性,而不是完全的按照規律,雖然沒有嘗試但是感覺完全的先随機後驗證在産生大量數獨時會有大量的沖突,是以考慮過預先存儲、随機讀取的方式。但是事實很快就告訴我,沒有調查的實踐最終很可能打臉。現在想想當時的行為略顯天真:試圖用回溯法把所有的數獨終局生成出來,存在一個檔案裡,需要時随機生成一個index去檔案中讀取相應的行。後來過了很久發現仍然隻是後面幾行在發生變化,再這樣下去可能C槽盛不下。去網上查了一下發現全部數獨的數量是一個極其驚人的數字,甚至連多少位都沒有數清,生成的檔案能不能放得下先不說,可能檔案讀寫花費的時間就讓人很難承受了。
1.0夭折了,但是當時并沒有意識到檔案讀寫的成本,是以仍然不死心的做了1.5,把1-9的全排列生成後存到檔案裡,随機取出來填到第一行裡并作為回溯的依據。第一次送出的就是這一版,理論上似乎比最開始的想法現實了一點,但是非常非常慢,親測不可用。
-
在前一個版本失敗後,基本上放棄了完全随機的想法,而是小範圍的随機。即随機生成一個以9開頭的1-9的排列作為初始數組,以此作為回溯的依據,一直回溯下去。經過數學計算,左上角第一格固定的話能夠生成的不重複的數獨是遠遠超過1000,000這個數字的,是以就采用了這樣的方法。
回溯的具體過程用到row,column, square三個9 * 9的數組做标記,記為1,記錄每一行、列、九宮格中已使用的數字在初始數組中的index。一個循環結束後回退時把标記抹去。
在求解數獨時也是用了相同的方法,但是由于存在原始值,與原始值存在相關的标記不能抹去,為了差別,記為2。但是這裡犯了一個嚴重的錯誤,直到第三版和測試才發現,遇到原始值應該直接跳過,但是這裡把原始值的判斷這一步寫進了循環裡,導緻回退之後原始值被修改。
- 第三個版本中回溯法失去了主導地位,是在D同學的建議下做出的改進,在此非常感謝D同學,這一部分會在性能改進中詳細說。
-
- 檔案輸入輸出
- 最開始使用了逐個字元輸入輸出的方法,感覺1000,000個數組可能一小時都完不成。
- 後來改成了每個數獨終局輸出一次的方法,發現幾乎沒有什麼改進。
性能改進
以下是優化後的CPU使用率s。
生成1000,000個數獨終局需要4分10s,雖然還是很慢,但是比最開始已經好了很多。
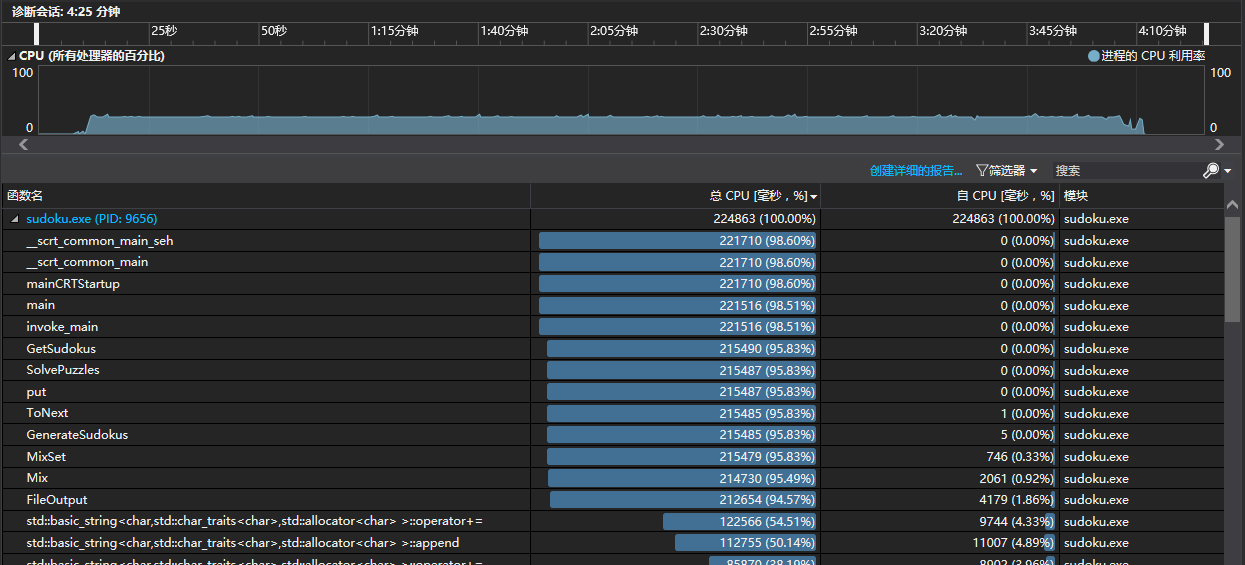
求解1000個數獨花費的時間約為38s,檔案輸入輸出更改後速度也提高很多。
單元測試,分别針對參數以及求解過程中的傳回值所表示的運作情況測試
運作過程中函數的消耗
檔案輸入輸出更改之後可以在10s内完成。
<ul>
<li>數獨生成方法的改進
<ol>
<li>左上角第一格為9,是以先把9個9放到合法的位置中(回溯)</li>
<li>随機産生初始數組,用求解數獨的方法(回溯)得到一個數獨</li>
<li>周遊1-8的全排列,由初始數獨進行映射,一個初始數獨可以得到8!個數獨</li>
<li>若已達到N則停止,否則傳回第一步</li>
</ol>
<p>由每個初始數獨産生的8!個數獨是不重複的,另外9個9個位置不同也能夠保證每個初始數獨産生的數獨都不重複。以下是流程圖:</p>
</li>
<li>檔案輸入輸出方法的改進
<p>在使用了每個終局輸出一次的方法之後發現輸出1000,000個終局仍然需要一小時以上的時間,于是打算将N個終局存在string中一次性輸出,将原來的輸出函數改成了将二維數組改為字元串的函數,在main函數的結尾一次性輸出</p>
<p>同理,也不再使用逐個字元讀入的方法,而是用了ifstream,stringstream和string一次将檔案中的内容讀到string中,再轉化為二維數組。後來發現string的拼接占用了大量的時間,于是直接使用字元數組,性能有了很大的提高。</p>
</li>
</ul>
代碼說明
- 生成左上角第一格數字的分布
int GetSudokus(int i, int **sudoku, int *row, int *col, int *squa) { int t = 0, j = 0, sign = 0; for (j = 0; j < 9; j++) { t = i / 3 * 3 + j / 3; if (row[i] != 0 || col[j] != 0 || squa[t] != 0) { continue; } sudoku[i][j] = FIX; row[i] = col[j] = squa[t] = 1; if (i == 8) { sign = SolvePuzzles(CopyArray(sudoku), "sudoku.txt"); } else { sign = GetSudokus(i + 1, sudoku, row, col, squa); } if (sign == -1) { return sign; } sudoku[i][j] = row[i] = col[j] = squa[t] = 0; } return sign; } - 将分布作為要求解的數獨,進行标記
int SolvePuzzles(int **puzzle, char *path) { int **row = CreateArray(), **column = CreateArray(), **square = CreateArra (); int i = 0, j = 0, t = 0; int *initSet = InitSet(); for (i = 0; i < 9; i++) { for (j = 0; j < 9; j++) { t = i / 3 * 3 + j / 3; if (puzzle[i][j] != 0) { row[i][puzzle[i][j] - 1] = 2; column[j][puzzle[i][j] - 1] = 2; square[t][puzzle[i][j] - 1] = 2; } } } int sign = GenerateSudokus(initSet, row, column, square, puzzle, 0, 0, path); DeleteArray(row); DeleteArray(column); DeleteArray(square); return sign; } - 求解初始數獨
int GenerateSudokus(int *initSet, int **row, int **column, int **square, int **sudoku, int i, int j, char *path) { int sign = 0; if (sudoku[i][j] != 0) { sign = ToNext(initSet, row, column, square, sudoku, i, j, path); } else { int k = 0, t = i / 3 * 3 + j / 3; int l = 0; for (k = 0; k < 9; k++) { l = initSet[k]; if (row[i][k] != 0 || column[j][k] != 0 || square[t][k] != 0) { continue; } else { sudoku[i][j] = l; row[i][k] = column[j][k] = square[t][k] = 1; sign = ToNext(initSet, row, column, square, sudoku, i, j, path); if(sign != 0){ return sign; } } row[i][k] = (row[i][k] == 2) ? 2 : 0; column[j][k] = (column[j][k] == 2) ? 2 : 0; square[t][k] = (square[t][k] == 2) ? 2 : 0; sudoku[i][j] = 0; } } return sign; } int ToNext(int *initSet, int **row, int **column, int** square, int **sudoku, int i, int j, char *path) { int sign = 0; if (j == 8) { if (i == 8) { if (mode == 'c') { sign = MixSet(CreateSet(8), 0, CreateSet(8), sudoku, CreateArray()); } else { FileOutput(path, sudoku); sign = -2; } if (sign == 0) return -2; } else { sign = GenerateSudokus(initSet, row, column, square, sudoku, i + 1, 0, path); } } else { sign = GenerateSudokus(initSet, row, column, square, sudoku, i, j + 1, path); } return sign; } - 生成映射集合
int MixSet(int *mixSet, int i, int *set, int **puzzle, int **out) { int j = 0, sign = 0; for (j = 0; j < 8; j++) { if (set[j] != 0) { continue; } mixSet[i] = j + 1; set[j] = 1; if (i == 7) { sign = Mix(puzzle, mixSet, out); } else { sign = MixSet(mixSet, i + 1, set, puzzle, out); } if (sign == -1) return sign; set[j] = 0; } return sign; } - 對初始數獨進行映射
int Mix(int **puzzle, int *minSet, int **out) { int i = 0, j = 0; for (i = 0; i < 9; i++) { for (j = 0; j < 9; j++) { if (puzzle[i][j] == 9) { out[i][j] = puzzle[i][j]; } else { out[i][j] = minSet[puzzle[i][j]-1]; } } } n++; FileOutput("sudoku.txt", out); if (n >= N) { DeleteArray(out); return -1; } return 0; }
實際時間
| PSP2.1 | Personal Software Process Stages | 預估耗時(分鐘) | 實際耗時(分鐘) |
|---|---|---|---|
| Planning | 計劃 | 30 | |
| | | ||
| Development | 開發 | 690 | 1080 |
| | | 150 | 180 |
| | | 60 | 40 |
| | | 50 | |
| | | ||
| | | 120 | |
| | | 90 | 240 |
| | | ||
| | | ||
| Reporting | 報告 | ||
| | | ||
| | | ||
| | | ||
| Sum | 合計 | 900 | 1350 |
總結
- 程式設計基礎太差:
- Bug具有反複性,仍然會出現與"==","||"相關的錯誤
- 邏輯不清晰,回溯法仍然需要大量的調試才能正确
- 時間規劃不合理,前期準備工作太多,留給具體代碼實作和後期測試的時間不夠充足。
- 沒有充分的參考資料和進行調查,以至于高估了方案的可行性
- 基本沒有運用面向對象課程中學習的内容