項目源代碼的Github連結
https://github.com/yaoling1997/softwareFirstHomework
需求分析
一、生成數獨
指令:sudoku.exe -c n
要求:
(1)輸出到sudoku.txt
(2)不重複
(3)1<=n<=1000000
(4)可以處理異常情況,如:sudoku.exe -c abc
(5)左上角第一個數為(學号後兩位相加)% 9 + 1=(9+9)%9+1=1
(6)參數不合法輸出"invalid parameters"到檔案
二、求解數獨
指令:sudoku.exe -s absolute_path_of_puzzlefile
(2)0代表空格
(3)檔案中數獨題目數為n,1<=n<=1000000
(4)保證格式正确
(5)對每個數獨題目求出一個可行解
解題思路
第一步想到的是通過枚舉每個格子的數字來生成數獨,但是顯然效率太低。通過上網查閱數獨的相關知識,其中有一篇部落格http://mouselearnjava.iteye.com/blog/1941483講到了通過轉換法來生成數獨。
第一種方法是交換數字法,比如說将棋盤上所有1和9互換位置後仍然是一個可行的數獨。
第二種方法是交換行列法,行和列的轉換,需要保證的是:交換隻發生在前三行,中間三行,最後三行,前三列,中間三列以及最後三列之間。而不能越界交換,比如第一行和第四行交換就是不允許的。 還有其餘的一些方法,不過這裡用不到。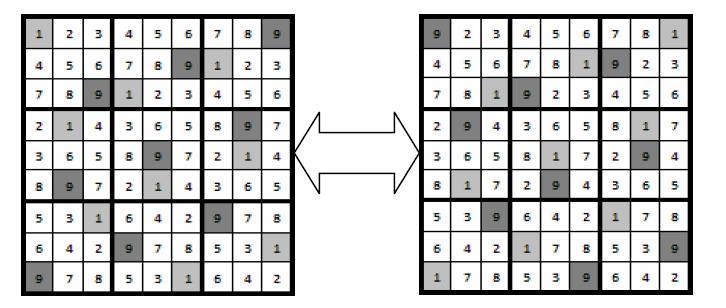
個人項目-數獨 
個人項目-數獨 經過和室友們的讨論,我們發現了一種基于變換來生成矩陣的方法。假設我們有一個正确的數獨,我們可以通過數字交換法,将1~9分别映射到不同的排列來生成另外9!-1個數獨。不過我們的題目要求左上角那個數字是固定的,于是通過第一種方法實際上共有8!=40320種數獨,暫且稱它們為種子。可題目要求最多可是要生成一百萬個數獨啊,怎麼辦呢?别急,接下來我們可以對這8!個種子應用行變換法。為了保證左上角的那個數字固定,我們做行變換時不考慮第一行。每3行分為一個組,第一組有不交換2、3行和交換2、3行兩種方法,第二組和第三組都可以采取映射的方式,分别有3!=6種方法,是以對于第一種方法生成的每一個種子,我們可以再生成2*6*6-1=71個數獨。是以我們一共生成了8!*2*3!*3!=2903040 種數獨滿足題目的數量要求。你可能會問,之後生成的數獨會重複嗎?我可以大聲告訴你,不可能。不同的種子之間第一行是不一樣的,是以它們通過行交換法生成的新數獨也不會重複。
一開始想到的是暴力枚舉沒有填數的地方,不過還是上網查閱一下資料比較好。這裡有一篇部落格http://www.cnblogs.com/grenet/archive/2013/06/19/3138654.html講的比較詳細。不過這篇部落格用到的求解方法仍然是比較低端的暴力,隻是有一些小優化。我在求解的時候先将所有的沒填數字的格子存到一個棧中,找出每個格子可以填的數字,存放到對應的set中。在搜尋的時候先從可填數字少的空格開始搜尋,這樣的話一旦這個格子填上數字後會使得剩下的某些格子可填的數字變少,進而可以更快地求出解。測試了一下10000組随機資料要跑74s左右。當然還有一些更高端的做法,比如說将數獨轉化為精确覆寫問題并用DLX算法求解。我是參考的劉汝佳大佬寫的白書(算法競賽入門經典——訓練指南)寫的,不過經測試對于自己構造的10000組随機資料DLX算法要跑109s,比一開始寫的暴力都慢,不過DLX的最壞求解時間是要優于暴力的。小夥伴們可以嘗試交一發poj3074,這題我寫的DLX可以過但暴力過不了。不過最終我還是決定交暴力,是以DLX算法在這裡就不過多叙述了。
本來是決定交暴力的,但是發現DLX慢是因為自己寫的太醜了,用性能分析工具一看發現自己用的vector特别耗時間,改成數組後效率有了質的飛躍。是以這裡還是簡單介紹一下DLX算法的實作。我是主要是參考了白書的算法。首先我們要知道什麼是精确覆寫問題(詳情可以參考http://www.cnblogs.com/grenet/p/3145800.html)

個人項目-數獨 有這麼一個矩陣我們要選擇一些行使得每一列有且僅有一個1
我們可以實作這麼一個連結清單

個人項目-數獨 第一行是建立的虛拟節點。每次遞歸時選擇節點數最少的一列,然後枚舉這一列上的行進行覆寫,記錄選擇的節點。覆寫的時候有會引起一些列的删除(所選行在對應列上有節點),這些新删的列有會引起一些行的删除(删除列在對應行上有節點)。遞歸會來有要還原連結清單的狀态。當連結清單隻剩下一個虛拟節點0時表示我們已經找到解了。
有了DLX算法,我們隻需要将數獨問題轉化為精确覆寫問題就可以求解了。精确在覆寫問題的矩陣中,行代表決策,列代表需要滿足的條件。我們可以将數獨問題轉化一下。(r,c,v)代表一個決策,在r行c列放數字v。需要滿足的條件可以表示為:slot(a,b),a行b列缺數字;row(a,b),a行缺數字b;col(a,b),a列缺數字b;sub(a,b),第a個小矩形缺數字b。每個決策滿足4個條件。是以連結清單一共9*9*9+1=729+1行(包括虛拟節點所占行),一共9*9*4=324列(不包括頭節點),總共不超過9*9*9*4+324+1=3241個節點。建構好連結清單後就可以套用DLX算法求解啦!
設計實作
c++中我直接用結構體來實作資料的組織,根據需求和實作方法的不同分為了三個結構體:SolveC、SolveS、DLX、SolveS_DLX
SolveC:解決生成數獨問題
其中包含三個函數,分别是:
(1)void initPermutation(int a[matrixLen])
用來生成用于映射的初始排列
(2)void rowChange(int row)
對目前種子進行行變換來獲得新的數獨,調用rowChange函數遞歸求解
(3)void solve()
解決問題的入口,調用initPermutation函數生成用于映射的初始排列,負責實作數字交換法,并調用rowChange函數來生成新的數獨
SolveS:解決求解數獨問題
其中包含五個函數,分别是:
(1)void init()
在求解每一個數獨問題前清空相應的資料結構
(2)void initSetOfThisEmptyPos(int x, int y)
對每一個空格求出初始狀态下所能填的所有數字,并放入它所對應的set中
(3)int removeItem(int x, int y, int xx, int yy)
在(x,y)上填上假想的數字後去更新空格(xx,yy)所對應的可填數字集合
(4)bool dfsSolve(vector<Node> emptyPos)
找到目前狀态下可填數最少的空格,調用removeItem函數對其它空格可填數集合進行更新,并調用dfsSolve函數遞歸求解問題
(5)void solve()
解決問題的入口,負責讀入資料(scanf),并調用相應的函數(init,initSetOfThisEmptyPos)給資料結構賦上初值,調用dfsSolve函數進行遞歸求解
DLX:解決精确覆寫問題
其中包含六個函數,分别是:
(1)void init(int n)
初始化連結清單和記錄每一列節點個數的數組S以及一些變量
(2)void addRow(int r, int columns[], int cnt)
添加一行節點到連結清單裡
(3)void remove(int c)
移除節點标号為c所在的列,并删除相應的行
(4)void void restore(int c)
恢複節點标号為c所在的列,并恢複相應的行
(5)bool dfs(int d)
調用dfs函數遞歸求解問題,調用remove函數删除列,調用restore函數恢複對應列
(6)bool solve(int ansRe[], int &ansSize)
解決問題的入口,負責調用dfs函數遞歸求解并傳回求出來的結果到ansRe中
SolveS_DLX:用DLX算法解決求解數獨問題
(1)int encode(int a, int b, int c)
給決策(a,b,c)編碼
(2)void decode(int code, int &a, int &b, int &c)
将編碼解碼成決策(a,b,c)
解決問題的入口,負責讀入資料(scanf),調用solver.init函數初始化DLX連結清單,調用solver.addRow函數添加一行節點,調用encode函數給決策編碼,調用solver.solve函數求解問題,調用decode函數解碼,通過output函數将結果輸出到檔案
流程圖
SolveC.solve():SolveS.solve():
個人項目-數獨 SolveS_DLX.solve():
個人項目-數獨 
個人項目-數獨
單元測試
單元測試中需要實作相應函數來判斷一個數獨終局是否合法,并對-c參數和-s參數分别測試代碼正确性。由于最後還是決定交DLX算法,于是把暴力的結構體代碼全部注釋掉了。
TEST_METHOD(TestMethod1)
{
SolveC solveC;
int a[matrixLen];
solveC.initPermutation(a);
//Assert::AreEqual(a[matrixLen-1],firstNum);
}
TEST_METHOD(TestMethod2)
{
SolveC solveC;
solveC.n = 2;
solveC.rowChange(3);
Assert::AreEqual(solveC.n, 0);
}
TEST_METHOD(TestMethod3)
{
SolveC solveC;
solveC.n = 200;
solveC.solve();
Assert::AreEqual(solveC.n, 0);
Assert::AreEqual(checkMatrix(solveC.newSeed), true);
}
TEST_METHOD(TestMethod4)
{
SolveC solveC;
solveC.n = 2000;
solveC.solve();
Assert::AreEqual(solveC.n, 0);
Assert::AreEqual(checkMatrix(solveC.newSeed), true);
}
TEST_METHOD(TestMethod5)
{
SolveC solveC;
solveC.n = 10000;
solveC.solve();
Assert::AreEqual(solveC.n, 0);
Assert::AreEqual(checkMatrix(solveC.newSeed), true);
}
TEST_METHOD(TestMethod6)
{
SolveS_DLX solveS;
freopen("C:/Users/acer-pc/Desktop/git/softwareFirstHomework/sudoku/sudoku/1.in", "r", stdin);
solveS.solve();
Assert::AreEqual(checkMatrix(solveS.matrix), true);
}
TEST_METHOD(TestMethod7)
{
SolveS_DLX solveS;
Assert::AreEqual(solveS.encode(2,4,8),207);
}
TEST_METHOD(TestMethod8)
{
SolveS_DLX solveS;
int a, b, c;
solveS.decode(207,a,b,c);
Assert::AreEqual(a, 2);
Assert::AreEqual(b, 4);
Assert::AreEqual(c, 8);
}
TEST_METHOD(TestMethod9)
{
DLX solve;
solve.init(5);
Assert::AreEqual(solve.sz,6);
}
TEST_METHOD(TestMethod10)
{
Assert::AreEqual(firstNum,1);
}

個人項目-數獨
覆寫率分析
可以看到實作功能的頭檔案solver.h的覆寫率為百分之百
個人項目-數獨
性能分析與代碼改進
設定參數為 “-c 1000000”
第一次運作的耗時為27.509秒

個人項目-數獨 可見耗時最多的函數是output函數,output函數裡我用putchar()函數逐個字元輸出。
我把輸出函數單獨提出來在VS上建立項目并測試,發現耗時為19.035秒。我換了個IDE平台進行測試,發現隻需要1.931秒
無奈把輸出方式成了fputs輸出,運作耗時變為了15.243秒

個人項目-數獨 貌似還是不夠快,從上圖我們可以看出swap()函數是相當費時的。
找到用到swap函數的地方,改成了手寫的交換元素,程式跑得更快了,耗時3.435秒

個人項目-數獨 設定參數為 “-s 1.in”
1.in中有4000組随機資料,第一次運作的耗時為47.113秒
從上圖可以看出vector的push_back相當耗時,于是我嘗試着把vector全部替換為數組。哇,太神奇了,盡然隻需要0.787秒!
個人項目-數獨 
個人項目-數獨
代碼說明
const int seed[matrixLen][matrixLen] = {
{ 1, 2, 3, 4, 5, 6, 7, 8, 9 },
{ 4, 5, 6, 7, 8, 9, 1, 2, 3 },
{ 7, 8, 9, 1, 2, 3, 4, 5, 6 },
{ 2, 1, 4, 3, 6, 5, 8, 9, 7 },
{ 3, 6, 5, 8, 9, 7, 2, 1, 4 },
{ 8, 9, 7, 2, 1, 4, 3, 6, 5 },
{ 5, 3, 1, 6, 4, 2, 9, 7, 8 },
{ 6, 4, 2, 9, 7, 8, 5, 3, 1 },
{ 9, 7, 8, 5, 3, 1, 6, 4, 2 }
};
進行變換前需要一個正确的數獨種子,從網上獲得
void rowChange(int row) {
if (row >= matrixLen) {
output(newSeed);
n--;
return;
}
int per[3];
for (int i = 0; i < 3; i++)
per[i] = row + i;
do {
int temp[3][matrixLen];
for (int i = row; i < row + 3; i++) {
memcpy(temp[i % 3], newSeed[per[i % 3]], sizeof(temp[0]));
}
for (int i = row; i < row + 3; i++) {
swap(temp[i % 3], newSeed[i]);
}
rowChange(row + 3);
if (!n)
return;
for (int i = row; i < row + 3; i++) {
swap(temp[i % 3], newSeed[i]);
}
} while (next_permutation(per, per + 3));
}
行從0開始标号,這是對3,4,5和6,7,8行的變換進而生成新的數獨
while (n > 0) {
for (int i = 0; i < matrixLen; i++)
for (int j = 0; j < matrixLen; j++) {
newSeed[i][j] = trans[numToPos[seed[i][j]]];
}
rowChange(3);
if (!n)
break;
swap(newSeed[1], newSeed[2]);
rowChange(3);
next_permutation(trans, trans + matrixLen - 1);
}
對每個種子,都采用行變換來生成新的數獨,通過algorithm庫中的next_permutation函數來生成下一個全排列
void addRow(int r, int columns[], int cnt) {
//r 行号,columns存放這一行的哪些列為1
int first = sz;//sz 目前建立節點标号
for (int i = 0; i < cnt; i++) {
int c = columns[i];
L[sz] = sz - 1;
R[sz] = sz + 1;
D[sz] = c;
U[sz] = U[c];
D[U[c]] = sz;
U[c] = sz;
row[sz] = r;
col[sz] = c;
S[c]++;
sz++;
}
R[sz - 1] = first;
L[first] = sz - 1;
}
往DLX的連結清單中添加一行節點,修改對應的指針(這裡是數組模拟連結清單)
#define FOR(i,A,s) for(int i= A[s];i!=s;i=A[i])
順着連結清單A,周遊除s外的其它元素
void remove(int c) {
L[R[c]] = L[c];
R[L[c]] = R[c];
FOR(i, D, c)
FOR(j, R, i) {
U[D[j]] = U[j];
D[U[j]] = D[j];
--S[col[j]];
}
}
移除标号為c的節點所在的列
void restore(int c) {
//恢複标号c所在的列
FOR(i, U, c)
FOR(j, L, i) {
++S[col[j]];
U[D[j]] = j;
D[U[j]] = j;
}
L[R[c]] = c;
R[L[c]] = c;
}
恢複标号c所在的列,注意恢複的順序與移除的順序相反
int encode(int a, int b, int c) {
return (a * matrixLen + b) * matrixLen + c + 1;
}
将決策(a,b,c)進行編碼,映射到對應的行号上
void decode(int code, int &a, int &b, int &c) {
code--;
c = code%matrixLen;
code /= matrixLen;
b = code %matrixLen;
code /= matrixLen;
a = code;
}
将code解碼獲得決策(a,b,c),用于獲得答案矩陣
for (int r = 0; r < matrixLen; r++)
for (int c = 0; c < matrixLen; c++)
for (int v = 0; v < matrixLen; v++) {
if (matrix[r][c] == 0 || matrix[r][c] == v + 1) {
int columns[10];
int cnt = 0;
//列号從1開始
columns[cnt++] = encode(SLOT, r, c);
columns[cnt++] = encode(ROW, r, v);
columns[cnt++] = encode(COL, c, v);
columns[cnt++] = encode(SUB, r / 3 * 3 + c / 3, v);
solver.addRow(encode(r, c, v), columns, cnt);
}
}()
枚舉決策(r,c,v),向連結清單中逐行添加節點,每個決策對應四個可滿足的條件(SLOT,ROW,COL,SUB)
表格
| PSP2.1 | Personal Software Process Stages | 預估耗時(分鐘) | 實際耗時(分鐘) |
|---|---|---|---|
| Planning | 計劃 | 60 | 30 |
| · Estimate | · 估計這個任務需要多少時間 | ||
| Development | 開發 | 5700 | 2820 |
| · Analysis | · 需求分析 (包括學習新技術) | 480 | 360 |
| · Design Spec | · 生成設計文檔 | 180 | |
| · Design Review | · 設計複審 (和同僚稽核設計文檔) | ||
| · Coding Standard | · 代碼規範 (為目前的開發制定合适的規範) | ||
| · Design | · 具體設計 | 240 | |
| · Coding | · 具體編碼 | 1800 | 1200 |
| · Code Review | · 代碼複審 | 120 | |
| · Test | · 測試(自我測試,修改代碼,送出修改) | 600 | |
| Reporting | 報告 | 420 | |
| · Test Report | · 測試報告 | ||
| · Size Measurement | · 計算工作量 | ||
| · Postmortem & Process Improvement Plan | · 事後總結, 并提出過程改進計劃 | ||
| 合計 | 6120 | 3270 |
GUI展示

個人項目-數獨 采用QT+VS2017開發
程式一開始随機生成數獨題目,玩家可以用滑鼠點選挖空的地方,用鍵盤輸入數字。點選submit按鈕即可送出自己的答案。在按鈕旁邊會顯示文字提示玩家的答案是否正确。真是太好玩了,趕緊叫上小夥伴們一起哈皮吧!