你沒有弄錯!大型娛樂數學線上聚會 - 紀念馬丁·加德納的全球聚會即将到來。像往常一樣,由于時差,中原標準時間正好比亞特蘭大時間快12小時,是以它是中原標準時間10.19-10.25 A.M在0:00 a.m.,4:00 a.m.,8:00 a.m。
按照慣例,每次會議預計需要30-45分鐘。本次聚會的主題包括鋪位,折紙,魔術等,是以您可以選擇您感興趣的主題(您需要提前安裝SOOM,下載下傳文章末尾的連結)會議号碼93502013825)。
這裡有21個主題和他們的介紹,看看有什麼有趣!
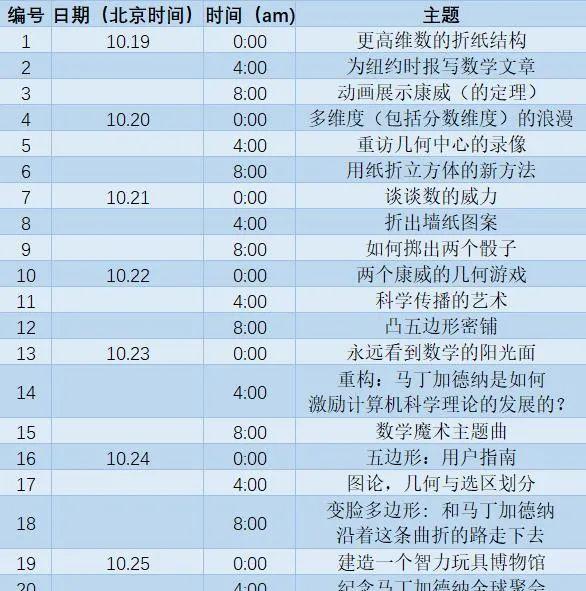
01 更高次元的折紙結構
2021年10月19日 0:00 中原標準時間上午
内容介紹:折紙是一門古老的藝術,發展至今,不斷帶給人們的藝術和科學見解。2012年,Buhler,Butler,de Launey和Graham通過建構受折紙啟發的數學結構來擴充這一想法。我們将這些代數和幾何學上先前已知的結果擴充到更高的次元。
嘉賓介紹:Adriana Salerno,來自委内瑞拉加拉加斯,2001年獲得西蒙玻利瓦爾大學數學學士學位,2009年獲得德克薩斯大學博士學位。她現在是緬因州一所小型文理學院貝茨學院的數學教授。Adriana Salerno的主要研究領域是數值理論,特别是數值理論與幾何,實體學,密碼學和編碼理論的交叉點。她還對數學交流和教學感興趣,并希望建立一個更具包容性和公平的數學社群。
02 為《紐約時報》撰寫數學文章
2021年10月19日 中原標準時間淩晨 4點00分
描述: 2010年春天,史蒂文·斯特羅加茨(Steven Strogatz)為《紐約時報》撰寫了15篇關于從基礎到進階數學元素的系列文章。在這次演講中,他将描述他給大衆帶來數學的曲折經曆,并将分享他的成功和失敗經驗。
嘉賓介紹:Steven Strogatz是康奈爾大學應用數學教授。他研究應用于實體學,生物學和社會科學的非線性動力學和複雜系統。他的新書《無限的力量》(Infinite Power)是《紐約時報》的暢銷書。
03 待定
2021年10月19日 8:00 中原標準時間上午
描述: 這裡將是約翰·康威(John Conway)巧妙理論的兩三個美麗的動畫證明。
嘉賓介紹:Burkard Polster是澳洲莫納什大學的數學家,在YouTube上主持Mathologer頻道。他盡最大努力追随馬丁·加德納的腳步,因為正是馬丁·加德納的文章激勵他成為一名數學家,并引導他學習數學,約翰·康威。
04 多元的浪漫,包括分數維
2021年10月20日 0:00 中原標準時間上午
描述: 尺寸似乎是一個直覺的概念。我們都熟悉零維點,一維曲線,二維曲面和三維實體。然而,次元是一個難以捉摸的概念,數學家們花了很多年的時間才弄清楚。我們将讨論次元的曆史,包括康托爾困擾數學家的發現,空間填充曲線的驚喜,公衆對第四次元的迷戀,時間作為額外次元,非整數次元的含義,以及高維空間的不可預測性。
嘉賓介紹:戴夫·裡奇森是迪金森學院的數學教授。他的研究興趣包括拓撲學,動力學,幾何學,數學史,有趣的數學,數學和藝術以及數學概述。他是"Ola的寶石:多面體公式和拓撲學的誕生"和"不可能的故事:2000年古代數學的探索"的作者,并擔任MAA(美國數學協會)數學視覺雜志的編輯六年。他從小就閱讀父親的馬丁·加德納(Martin Gardner)系列,并開始參加G4G11上的G4G(馬丁·加德納派對)。
05 重溫幾何中心的記錄
2021年10月20日 4:00 中原標準時間上午
内容:待定
嘉賓介紹:Tamara Munzner是不列颠哥倫比亞大學計算機科學教授。她于1991年至1995年在幾何中心工作,并于2000年獲得斯坦福大學博士學位。2014年,她出版了《視覺分析與設計》(Visual Analysis and Design),這是AK Peters Visual Series(CRC/Routledge Press)的第一部,并繼續擔任該系列的編輯。2015年,她被授予IEEE VGTC視覺技術成就獎。
06 在紙上折疊立方體的新方法
2021年10月20日 8:00 中原標準時間上午
描述: 什麼形狀的紙可以折疊成機關立方體?根據允許的折疊類型,這個看似簡單的問題可以有許多有趣的答案和擴充的開放問題。特别是,我們将看到一張3×3的正方形紙(6×6折痕)沿着水準,垂直,對角線折痕成一個機關立方體。(這是與Kingston Yao Czajkowski等人合作的結果。
嘉賓介紹:Erik Demaine是麻省理工學院的計算機科學教授。Erik的研究興趣跨越了算法領域,從改進網絡搜尋的資料結構到了解蛋白質如何折疊的幾何形狀,再到玩遊戲的計算難度。他獲得了麥克阿瑟獎:"計算機幾何學家能夠逐一處理和解決與折疊和彎曲有關的問題,在理論和娛樂之間輕松切換,并且熱衷于在娛樂中發現理論。他出現在折紙紀錄片"褶皺之間"和NOVA的"折紙革命"中;他與人合著了一本關于折疊理論的書《幾何折疊算法》(Geometric Folding Algorithms)和一本關于遊戲計算複雜性的書《遊戲、拼圖和計算》(Games, Puzzles, and Computings)。與他的父親馬丁一起,他的興趣跨越了數學和藝術,他的作品,彎曲的折痕雕塑,被紐約現代藝術博物館和史密森尼的倫威克畫廊永久收藏。
07 談論數字的力量
2021年10月21日 中原標準時間淩晨 0點00分
大約在1502年,盧卡·帕斯喬利(Luca Pascioli)寫了一本書《數字的力量》(The Power of Numbers),其中包含數學問題、謎題等等。這本大集的書籍,我們第一次聽到。雖然它即将出版,但它一直以手稿形式保留到20世紀。讓我們來看看這本書,裡面有200多個數學謎題,以及它的曆史和作者。
嘉賓介紹:Tiago Hirth(蒂亞戈)赫斯是裡斯本中央大學科學技術研究中心資助的博士學者。他目前是Gardner Gathering G4G基金會的顧問,也是Fun Math雜志的副主編。他喜歡做有趣的數學,棋盤遊戲研究和魔術藝術的研究,當他不做科學,表演魔術,幫助Circo Matemático成長(他在2011年幫助建立了它),開一個工作室,組織會議或其他分心。
08 折疊出圖案桌面圖案
2021年10月21日 中原標準時間淩晨 4點00分
描述: 本講座将介紹通過折紙過程探索桌面組的案例研究。第一步是簡要介紹馬賽克圖案(和其他對稱圖案)的折疊技術,包括一些基本動作,這些動作可以組合産生任何複雜的視覺模式。在我們看來,馬賽克折紙為探索桌面組提供了一種特别有效的機制,因為它們通常允許在隻需要一張紙而不需要更多裝置的對稱組中手動實作(和反向)實體變化。認知和表演這種心理和觸覺體驗的變化可能有助于識别潛在的對稱結構。快速輕松地調整折痕圖可能會導緻數學上顯著的變化(例如,在保持旋轉對稱性的同時消除反射),或者保留原始桌面組但外觀發生重大變化的更改。演講将介紹桌面組分類的一些關鍵概念,但重點是玩紙。
嘉賓介紹:Rachel Quinlan是愛爾蘭戈爾韋國立大學的數學家。她于2000年獲得阿爾伯塔大學代數博士學位,目前的研究活動集中在矩陣理論和線性代數的結合上。她喜歡從紙上折疊對稱的圖案,你可以在Twitter上搜尋@rkquinlan。
09 如何擲兩個骰子
2021年10月21日 8:00 中原標準時間上午
說明:大富翁和卡坦島等遊戲玩家擲出一對六面骰子并使用結果的總和。有許多非标準骰子旨在提供相同的結果分布。一個著名的例子是由喬治·西奇曼上校發現并由馬丁·加德納推廣的西切曼骰子對(六個面中的一個面有1,2,2,3,3,3,4個點,其他六個面分别有1,3,4,4個點)5,6,8),由喬治·西奇曼上校發現并由馬丁·加德納推廣,是唯一一對異構骰子以正整數編碼六面骰子并具有與标準骰子相同的和分布。超過六面的骰子而不隻是求和,可以提供更多實作所需配置設定的方法,其中一些是記者發現的。
嘉賓介紹:亞曆山大·穆尼斯設計了許多謎題和骰子。
10 兩個康威幾何遊戲
2021年10月22日 中原標準時間淩晨 0點00分
描述: 約翰·康威喜歡探索三角形的不尋常本質,也喜歡探索密集商店的本質。他的兩個發現都是以他的名字命名的 - 康威圓定理和康威碼。我将讨論這兩個遊戲,其中一個遊戲導緻了一個新的緊湊型應用程式。
嘉賓介紹:摩拉維亞大學數學名譽教授Doris Schattschneider以其工作和關于密集商店工作的講座而聞名,尤其是圖形藝術家M。埃舍爾。作為約翰·康威40多年的朋友,她用這份報告紀念了他。
11 傳播科學的藝術
2021年10月22日 中原標準時間淩晨 4點00分
描述: 你如何講述科學的故事?在負責著名的pbs科學系列節目nova35年後,Paula Apsell将在電視和網絡上讨論科學交流的藝術。使用NOVA的片段,她将分享複雜的科學思想如何被接受和令人信服。
嘉賓介紹:Paula S. Apsell開始在波士頓電視訊道WGBH播出。1975年,她加入了科學紀錄片NOVA小組,該小組為電視和線上科學節目設定了标準,并制作了從人工智能和基因工程到航空安全等主題的紀錄片。1985年,在麻省理工學院擔任《科學新聞》成員一年後,她成為NOVA的進階執行制片人。2018年,她獲得了美國電影藝術與科學學院終身成就獎。她也是美國科學促進會的成員。
12 凸五角形密集攤鋪
2021年10月22日 中原標準時間上午 8:00
描述: 有豐富的數學曆史,鋪設凸五邊形的飛機,馬丁加德納和其他參與者扮演着關鍵角色。公衆可以欣賞結果所産生的問題和美麗的模式。所有這些密集的特征對數學科學都非常有益。對于動手示範,具有整數邊的密集切片示例可以簡化密集鋪路模式的建立。讓我分享一下确定具有整數邊的凸五邊形所涉及的數學原理,這些五邊形可以以密集的方式布局,這裡稱為"pintegons"。
嘉賓介紹:Glenn 惠特尼曾是金融分析師,是美國國家數學博物館的創始人,兼職大學數學教師,《數學願景》"遊樂場"專欄的編輯,Studioinfinity.org 網站的作者。
13 永遠看到數學的陽光
2021年10月23日 中原標準時間淩晨 0點00分
"有些人認為數學不好,這真的傷害了我 - 數學不僅僅是算術,"他說。數學無處不在,它很漂亮,我發誓。普及數學并不難。我總是看到數學積極的一面。我總是看到數學光明的一面。讓我們去波特蘭或聖地亞哥,加利福尼亞州,塔科馬,華盛頓特區.C,看看他們如何在公共場合玩遊戲,展示拼圖,模型和問題,并創造對數學的積極态度。這個地點(和涉及的人)清單并不詳盡,但它激勵我做更多的事情。也許它也會激勵你。
演講嘉賓:Jenny Quinn是美國數學協會主席,也是華盛頓大學塔科馬分校的教授。作為一名屢獲殊榮的教師,學者和作家,Jenny緻力于使數學易于了解,欣賞和人性化。在新冠爆發期間,tacomamath團隊為不同級别(電子和印刷)建立了數學任務,在戶外用粉筆編寫遊戲,并制作了Youtube短視訊,以鼓勵社群成員熱愛數學文化。同樣為了應對疫情,Jenny開始在部落格上寫"新皇冠上的數學"(https://mathinthetimeofcorona.wordpress.com/),記錄她的遠端數學教學,保持受歡迎程度,建立孤立的社群,以及冠狀病毒病對我們個人和職業生活的持續影響2019年。作為一名作品集學者,Jenny認為,美的證明既是藝術,也是科學。她最近一直在研究藝術,作為交流數學的一種手段,我們将在今天的演講中聽到一些關于它的資訊。
14 重建:馬丁·加德納是如何激發計算機科學理論發展的?
2021年10月23日 中原標準時間淩晨 4點00分
内容:在過去的10到15年中,理論計算機科學的一個流行領域是"組合重構"或"重構"。馬丁·加德納(Martin Gardner)對這一領域的貢獻尚未得到廣泛了解。我即将證明重構的根本問題 - 本質上是一個"移動硬币難題" - 起源于G4G6的交換禮物!
嘉賓介紹:鮑勃·迪倫·赫恩在馬丁。加德納與《科學美國人》一起長大,這使他對數學和拼圖産生了終生的熱愛,為他赢得了麻省理工學院的博士學位,并與Erik Demaine共同出版了有關遊戲,拼圖和計算的書籍。然後,他與人共同編寫了曾經流行的Mac程式Clarisworks,并開始為許多其他軟體公司工作。鮑勃的另一個愛好是參加超級馬拉松比賽,在那裡他擁有多項美國年齡組紀錄。Bob自2002年以來一直參加第四屆馬丁·加德納派對,自2015年以來一直擔任G4G項目的主席和主持人。
15 數學魔術主題曲
2021年10月23日 中原標準時間上午 8:00
描述: 我會執行 - 并解釋!一些基于有趣的數學原理的魔法被揭示出來。
嘉賓介紹:馬特·貝克(Matt Baker)白天是佐治亞理工學院國際知名的數學教授,晚上是一位多才多藝的魔術師。Matt于1999年獲得加州大學伯克利分校數學博士學位,并于2011年晉升為佐治亞理工學院的全職教授。他出版了三本數學書籍和40多篇研究論文,是一位受歡迎的數學部落客,也是美國數學學會的成員。Matt對教學的熱情為他赢得了無數獎項,包括佐治亞理工學院CETL / BP初級教師教學獎和佐治亞大學系統委員會教學卓越獎。Matt現在是佐治亞理工學院教師發展系的副院長。馬特在他的魔法生涯中也赢得了贊譽。馬特曾兩次在亞特蘭大獲得年度魔術師大獎,并三次受邀參加費希特在世界上第一次特寫魔術會議上的手指輕拂表演。馬特的魔術已經出現在幾個國家期刊上,2019年他出版了他的第一本原創魔術書Buena Vista Shuffle Club。世界著名的魔術師約書亞·傑伊(Joshua Jay)稱其為"一本優秀,有趣,個人的魔術書集,閱讀起來很有趣。"
16 五角大樓:使用者指南
2021年10月24日 中原標準時間淩晨 0點00分
内容介紹:正面五邊形在密集鋪路時會有缺口,但不要讓這個例子玷污五角大樓的良好口碑!來吧,讓我們來探索這15個不規則的五邊形,它們可以布置在一個緊密的平面上,跨越五個對稱性,快速瞥見單緊瓷磚,當然還有分形。準備好在這個完整的五邊形手冊中找出所有有趣的和關于五件事的五件事!
嘉賓介紹:Ayliean Macdonald是一位數學老師,緻力于以創新的方式探索,解釋和激發學生對數學的興趣。她的特征通常反映在使用模型和分形的延時繪圖來顯示數學對象靜止圖像不可見的變化和漸進過程。
17 圖論、幾何和選區劃分
2021年10月24日 中原標準時間淩晨 4點00分
描述: 當你想劃分一個州以獲得投票權時,劃定邊界的方法是什麼?如果你找不到所有的方法,你能選擇一個很好的例子嗎?我将讨論一些非常簡單的圖形和幾何問題,這些問題可能有助于我們在政策和民主選舉中取得進展。
嘉賓介紹:Moon Duchin是塔夫茨大學的數學教授,也是Tisch College公民生活的進階研究員。她創立了公制幾何和選區重劃小組,該小組使用幾何和計算來研究重新劃分選區和投票權。她是美國數學學會的成員,并于2018年獲得古根海姆學者獎和拉德克利夫獎。
18 改變面孔的多邊形:馬丁·加德納沿着這條曲折的道路走下去
2021年10月24日 中原標準時間上午 8:00
描述: 故事始于1959年,當時馬丁·加德納(Martin Gardner)向我介紹了變臉多邊形,這是一種無限折疊的紙質玩具。在1961年發現另一個改變面孔的四人組後,我渴望講述這個故事。基于一系列變臉四邊形,我提出了我的和諧變臉理論,我發現它們在少量的重新定義下對應于五幀多米諾骨牌。然後我發現面部變化的六邊形是相同的,将兩個面部變化模型放在同一平面上,并且它們具有許多共同的屬性。我會告訴你如何讓它們來證明我的理論。在學習了彭羅斯馬賽克之後,我在2006年制作了最美麗的彭羅斯瓷磚拼圖,我的願望上升到頂峰,向這些特别的客人展示我的彭羅斯馬賽克着色概念。我希望去亞特蘭大參加G4G14,并使用變臉多邊形作為展示我的Penrose作品的工具。我會把其中一些作品和其他我想在我的展台上展示的藝術作品。www.r2d3.com 通路我的網站,了解在發送邀請之前編寫的本示範文稿的大部分内容。
嘉賓介紹:Red Deupree接受過科學家教育訓練。小時候,他立志成為一名發明家或科學家(那些穿着白色實驗室外套的人)。30歲時,他遇到了一台電腦,像魚一樣喝水。他以編寫和維護定制軟體和資料庫為生,首先是福特,然後是R2D3。退休後,他編寫了應用程式,使彭羅斯瓷磚着色系統标準化。當他了解G4G時,他想出了用變臉四邊形呈現Penrose藝術品的想法,并寫了一個設計變臉六邊形的應用程式。在G4G因為新冠爆發延遲的情況下,他将和諧面六邊形理論标準化,并将在這裡展示。
19 建立智力玩具博物館
2021年10月25日 0:00 中原標準時間上午
描述: 建造一個具有"展示和遊戲"的智力玩具博物館對于大約10個智力玩具來說很容易,但對于50,000個智力玩具來說卻具有挑戰性。
嘉賓介紹:喬治·米勒(George Miller)研究人工智能,并在美國銀行(Bank of America)擔任全球外彙系統。在大規模營銷之前,他喜歡在玩具上市之前設計它們。羅克珊·米勒研究曆史。她在香港擔任英語老師。她的愛好是收集智力玩具,如魔方,魔法金,異國情調的拼圖和水晶拼圖。
20紀念馬丁·加德納的全球聚會
2021年10月25日 中原標準時間淩晨4點00分
描述: 派對之是以如此愉快,是因為我們分享時間,交流想法和想法。本着這種精神,我們邀請來自世界各地的您加入我們,以誇張的笑話,魔術和特技。
嘉賓介紹:來自俄克拉荷馬州諾曼市的吉姆·加德納(Jim Gardner)将帶來一個有趣的加德納笑話。來自加拉加斯的Rafael benatar,來自慕尼黑的Thomas fraps,來自法蘭克福的Pit Hartling,來自以色列的Lior莊園,來自洛杉矶的Norman Gilbreath(由來自斯克内克塔迪的Gordon Bean主持)和來自紐約的Mark Mitton。來自palo alto的Tadashi tokieda将展示一個美妙的新數學娛樂小工具,speedcubers。Lucas Garron和Cary Huang将向我們展示一些令人眼花缭亂的魔方快速擰緊技術。
21 與數學家一起旅行
2021年10月25日 8:00 中原標準時間上午
描述: 在1960年代和1970年代,大衛·亨德森(1939-2018)是一位著名的拓撲學家。然而,他告别了純粹的理論空間,轉向了數學教育。他認為自己是一個幾何學家,是《體驗幾何學和微分幾何:幾何學導論》一書的作者。鮑勃·摩西(1935-2021)邀請他為代數項目設計幾何材料。這個講座是關于我和大衛·亨德森的旅行,他教我如何觀察數學的無處不在。
嘉賓介紹:Dania Temina出生于拉脫維亞裡加。她曾在拉脫維亞大學和康奈爾大學教授各種數學課程。她是著名的雙層編織的先驅,她的書《雙面編織之旅》是衆所周知的。她最初的數學模型将她引入編織領域,她的作品曾在多個藝術展覽中展出。
本文由Martin Gardner的黨網站編譯和翻譯:
https://www.gathering4gardner.org/g4gs-celebration-of-mind-2021-10/
并參考百度翻譯等軟體。由于水準有限,時間倉促,不當請了解。希望您分享此活動!
最後附上:ZOOM下載下傳連結(可複制并粘貼到浏覽器):
1. 電腦端
http://www.miiyun.cn/download/276280?module=soft&id=276280&token=ba9d2a3c7a1fdd9f69776a585687df53&isxzq=0
2.手機端
https://zoom.us/client/latest/zoom.apk
數學卓越
高中生人才計劃
數學官方公衆号
推送數學數學課程和學習材料