Selected from arXiv
Author: Iddo Drori et al
Machine Heart Compilation
Machine Heart Editorial Department
Your exam papers may also be machine-generated.
Some time ago, a study by DeepMind appeared on the cover of Nature, solving two major mathematical problems by guiding intuition; after that, OpenAI taught GPT-3 to go online and use text-based web browsers.
On the last day of 2021, a joint research team from MIT with Columbia, Harvard, and the University of Waterloo published a 114-page paper proposing the first model that can automatically solve, score, and generate college-level mathematical problems at scale, arguably an important milestone in artificial intelligence and higher education. In fact, before this study, it was widely believed that neural networks could not solve advanced mathematical problems.
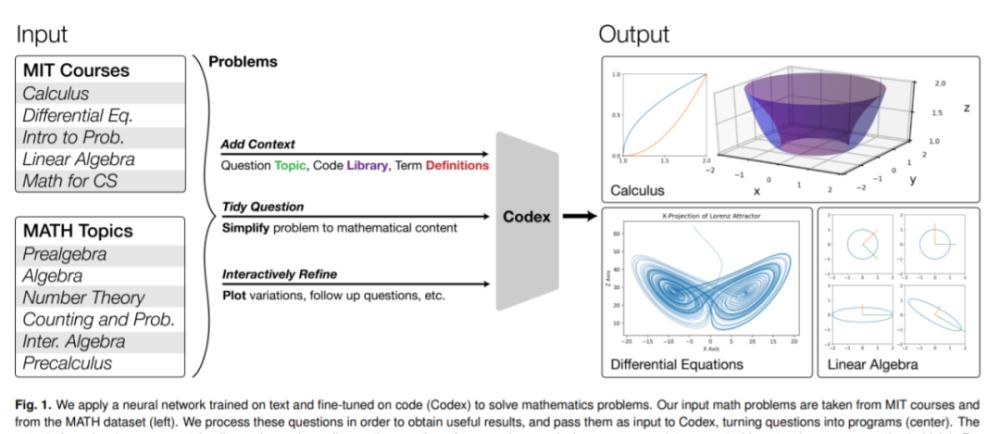
It is worth mentioning that the study used OpenAI's Codex.
How powerful is this research? Let's take the following diagram as an example, the following figure shows the calculation of the Lorenz attractor and its projection, the calculation and demonstration of the geometry of the Singular Value Decomposition (SVD) method, etc. Machine learning models have a hard time solving the above problems, but this study shows that they can solve not only these problems, but also the courses they belong to and many of these course problems at scale.
The study shows that neural networks that are pre-trained on text and fine-tuned on code can solve mathematical problems through program synthesis. Specifically, the study translates mathematical problems into programming tasks, automatically generates programs, and then executes them to solve MIT math course problems and problems from math datasets. Among them, the MATH dataset is the latest benchmark for higher mathematical problems specifically designed to evaluate mathematical reasoning, covering primary algebra, algebra, counting and probability, number theory and calculus.
In addition, the study explored a number of prompt generation methods that enabled Transformer to generate problem solvers for the corresponding topic, including solutions with images. By quantifying the gap between the original question and the translated cue, the study assessed the quality and difficulty of generating the question.
Address of the paper: https://arxiv.org/pdf/2112.15594.pdf
method
data set
The study first randomly selected 25 questions from each of the following six courses at MIT:
Univariate calculus;
Multivariate calculus;
Differential equations;
Introduction to Probability and Statistics;
Linear algebra;
Computer Science Mathematics.
For the MATH dataset, the study randomly sampled 5 questions from each topic and validated the results of the method beyond overfitting the training data through experiments on comS3251, a new course in applying linear algebra.
Method flow
As shown in Figure 2 below, the study uses Codex to convert course problems into programming tasks and run programs to solve mathematical problems. The following illustration contains a total of 5 A-E panels, and the left part of each panel shows the original question and the re-expressed hints, where the hints are formed by adding context, interaction, simplified descriptions, and so on.
The study translates from original course questions to Codex tips into three categories:
Native hints: Codex hints are the same as the original question;
Automatic prompt conversion: Codex prompts are different from the original question and are automatically generated by Codex;
Manual prompt conversion: Codex prompts are different from the original question and are generated manually.
The gap between questions and tips
The key to translating a problem into a Codex hint is the semantic proximity between the original question and the hint that produces the correct solution. To measure the gap between the original question and the success cue, the study used the cosine similarity between Sentence-BERT embeddings, as shown in Figure 3 below.
Sentence-BERT uses siamese and triplet neural network structures to fine-tune pre-trained BERT models. Crucially, Sentence-BERT is able to generate semantic embeddings at the sentence level, allowing semantic similarity comparisons between long texts.
In the study's experiments, the similarity between the original question and the prompts that generated the correct answer is shown in Figure 4 below.
Codex is used for prompt generation
In some courses, using the original question hint Codex without conversion does not produce the correct solution. Therefore, the original problem needs to be translated into a form that Codex can handle, mainly divided into the following three categories:
Topic context form: This form provides Codex with topics and subtopics related to general lessons and specific questions to help guide Codex in generating relevant and correct answers. For example, for conditional expectation problems in probability, it is helpful to provide contextual information about Bayes' theorem, expectations, and so on.
Library context: This form provides Codex with the programming packages/libraries needed to solve a given problem. For example, guide Codex to use numpy packages in Python to solve linear algebra problems.
Definition context: Many times, Codex's definition of certain terms lacks a realistic context. For example, Codex doesn't understand what Full House means in playing cards. So having Codex understand these terms and define them clearly can better guide its programming synthesis.
Generative problems as well as human assessments
The study used Codex to generate new questions for each course, using a dataset to create a numbered list of questions that would be truncated after generating a random number of questions, and the results would be used to prompt Codex to generate the next question. Repeating this process can create many new questions for each course.
The study conducted a long-term survey of students from MIT and Columbia universities who had taken these or equivalent courses. The purpose of the survey was to compare the quality and difficulty of machine-generated questions with manually written questions for each course. The study randomly selected five original questions and five generated questions for each MIT course. In the survey, students were asked to read ten questions from each course, which were a mixture of human-written and machine-generated questions.
For each of the 60 questions, students were asked three questions, as shown in Figure 5: whether they considered a given question to be (i) human-written or machine-generated, (ii) appropriate or unsuitable for a particular course, and (iii) what was the level of difficulty of the question in the range between 1 (easiest) and 5 (most difficult). Ask students to provide their grades on math problems instead of solving them. The survey is available online and anonymously.
Survey results
Problem solving
The researchers solved a total of 210 problems presented in the supplement, including 25 random problems for each of the 6 courses and 10 random problems for each of the 6 topics in the MATH dataset (elementary algebra, algebra, number theory, counting and probability, middle pole algebra, calculus).
Generate a new question
The researchers generated 120 new questions, including 10 new questions for 6 courses and 6 MATH topics. Table 2 below shows one generation question for each course and each MATH topic. Generating a question takes less than 1 second, and researchers can generate any number of questions. They created hints for 25 randomly selected questions that Codex was able to generate correct answers, cut into random questions, and let Codex complete the next new question.
Student survey results
The researchers said that a total of 13 participants completed a Q&A survey of all 60 questions, which took an average of 40 minutes. Figure 6 below summarizes the comparison of human-written and machine-generated problems in the student survey and yields the following results:
Machine-generated questions are more difficult than manually written questions, but within the confidence interval;
Manually written questions are more appropriate for the curriculum than machine-generated questions;
Manually written problems are more likely to be considered human-written, and machine-generated problems are treated as having the same probability of machine-generated and manual-written problems.
Answer grading
Codex is capable of answering all randomly sampled math problems in college-level and MATH datasets, whether they are in the original or collated state.
challenge
The researchers' approach also has some technical hurdles that cannot be solved.
1. Enter the image. One of the basic limitations of Codex is that it can only receive text-based input. As a result, Codex cannot use necessary visual components such as graphs or charts to answer questions.
2. Advanced mathematical proof. Another limitation of this study is the lack of proof of advanced mathematics. The researchers emphasize that this is due to the breadth of the study itself rather than the proof ability of Codex. The fact that most of the simple analytical proofs submitted to Codex in the study have been successfully executed is alarming because the proofs are not usually code-based.
3. Program evaluation. The final step in the study is to execute the program, for example using the Python interpreter. Students who take college-level courses also write code to solve some of their problems. Therefore, the study tested neural networks' problem-solving abilities in the same way as human students, allowing them to use the necessary tools. There is also work on neural program evaluation, demonstrating the use of machine learning to predict program output. LSTM is used to successfully predict the output of certain linear time and constant space programs (18). These have added memory scratchpads to allow for larger program categories (19). Recent methods use causal GNN (20) and transformer (21). Although evaluating arbitrary code is undecidable, special cases, such as a program generated by another transformer to solve a simple mathematical problem, should in principle be learnable.
4. Theoretical complexity. The results of the computational complexity show that the study was unable to solve every specific example of a general problem in a university math curriculum. For example, the following question has a difficult result to handle: Can vector v be represented as the sum of vectors from the collection S? What is the solution of the following first-order differential equation? However, we know that the problems given by assignments and exams can be solved by humans, so these complex results do not apply to the specific examples of the study to solve.
Quickly build an enterprise-grade TTS speech synthesis assistant with NVIDIA Riva
NVIDIA Riva is an SDK that uses GPU acceleration to rapidly deploy high-performance conversational AI services for rapid development of speech AI applications. Riva is designed to help you easily and quickly access sessionAL AI capabilities, out of the box, and quickly build high-level TTS speech synthesis services with a few simple commands and API operations.
January 12, 2022, 19:30-21:00, the main introduction of this online sharing:
Introduction to speech synthesis
Introduction to NVIDIA Riva features
Launch the NVIDIA Riva client to quickly implement text-to-speech functionality
Use Python to quickly build Riva-based TTS speech synthesis service applications