Apollo was a philosopher of ancient Greece who proposed such a theorem, which later generations named after him.
Apollo's theorem: The sum of squares of any two sides of a triangle is equal to half the square of the third side and twice the sum of the squares of its line.
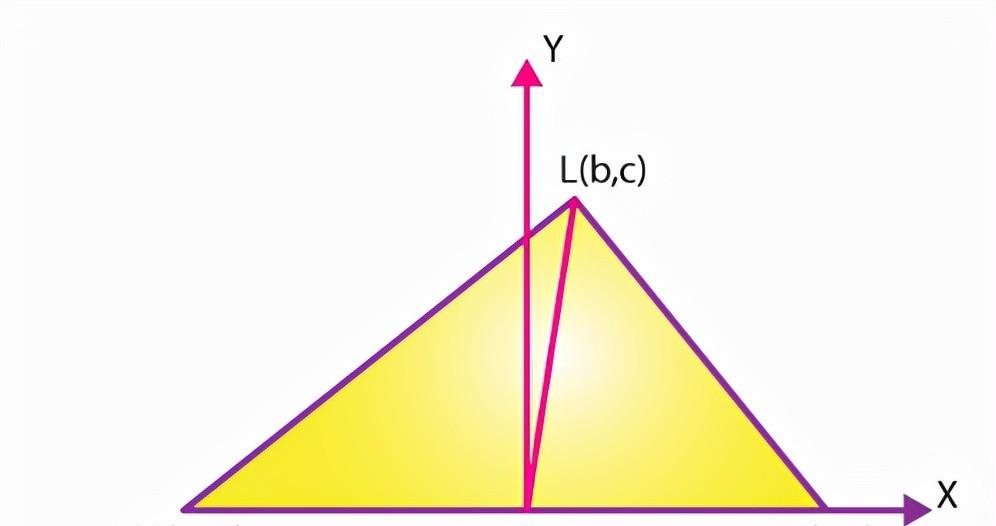
Evidence 1:
As shown in the figure, lo is the midline of the bottom side MN, then there is
Select the Cartesian coordinate origin at point O, the x-axis along the edge MN, and the y-axis is also OY. When MN = 2a, the coordinates of point M and point N are (a, 0) and (- a, 0), respectively. If the coordinates of point L are (b, c), then:
This proves the above theorem.
Evidence 2
There is also a proof method that uses the cosine theorem, as shown in the figure:
=+-2m.n.cos(180-a)
=+-2m.n.cos(a)
Add the above two equations:
+=2 (+)
The theorem is proved.
Evidence 3
Using the Pythagorean theorem, make the bottom of the perpendicular line, as shown in the figure:
=+
Add two equations left and right:
+=2+2+2
whereas
So there is
+=2(+) ,
Proof completed.
Using Apollo's theorem, the midline of a triangle can be found, given a trilateral. In the same way it can also find a diagonal line of a parallelogram if the other diagonal line is given and the two sides are known.
The inverse theorem of Apollo's theorem can be used to prove that quadrilaterals are parallelograms. If the sum of squares of the diagonal is satisfied, it is the sum of the squares of the four sides of the quadrilateral.
i.e. satisfied:
Then the quad is a parallelogram.
As shown in the figure:
The four sides of the quad are, p, q, r, s, and the length of the diagonal is x, y
Take the midpoint M, N of the diagonal line, according to the Apollo theorem:
That is, M and N coincide, that is, diagonally divided, so the quadrilateral is a parallelogram.