本節書摘來自華章出版社《計算機組成原理》一書中的第2章,第2.2節, 作 者 computer organization and architecture: themes and variations[英]艾倫·克萊門茨(alan clements) 著,沈 立 王蘇峰 肖曉強 譯, 更多章節内容可以通路雲栖社群“華章計算機”公衆号檢視。
用來計數的數字(即1,2,3,4,…)被稱作自然數,因為它們并不依賴于數學而存在——無論地球上是否有人去數,獵戶座的腰帶上總是3顆星。我們用十進制或十進制系統計數,因為它有0~9共10個符号(對應于人手指的個數)。
并非所有數字都是自然數。人們發明了負數來處理如銀行存款餘額等情況。還創造出實數描述123.456和13/14那樣的數。實數可分為有理數和無理數。有理數可被表示為分數(如7/12),而無理數不能被表示為一個整數除以另一個的形式,例如π或。
現代數字系統中,有一個符号表示0,這是在1400年前後由阿拉伯世界傳入歐洲的。該系統使用位置記數法表示十進制數,每個數位的值或權取決于它在數字中的位置,例如數1261中6的值就是數126中6的10倍。十進制數1261等于1×1000+2×100+6×10+1×1。在位置記數法中,當一個數隻剩一位時所乘的值稱作基數。
按照位置記數法,一個n位的整數n将按照下面的形式書寫:
<code>an-1, an-2,…, ai,…,a1a0</code>
這裡ai(i=0,1,...,n–1)是與b的幂相乘的系數(此處b為基數)。例如,當基數為10時,我們可以将n=278寫作a2a1a0,這裡a2=2,a1=7,a0=8。
用小數點(例如,十進制小數點基于十進制運算,而二進制小數點基于二進制運算)将整數部分和小數部分分開,可以對位置記數法進行擴充,使其能夠表示實數。十進制運算中的實數按照形如1234.567的方式書寫。一個小數點前有n位,小數點後有m位的實數被表示為an-1an-2…ai…a1a0.a-1a-2…a-m。
一個用基數為b的位置記數法表示的數的值被定義為:
<code>n = an-1bn-1+…+ a1b1+ a0b0+ a-1b-1+ a-2b-2+…+ a-mb-m</code>
=
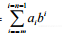
采用位置記數法,一個數的數值等于它各位值的總和,而每一位的值則是該位的數值乘以它在數中的位置所對應的權。例如,十進制數1982等于1×103+9×102+8×101+2×100。對于任意基數b,b0的值總是1。
當基數為2時,二進制數10110.11的值為1×24+0×23+1×22+1×21+0×20+1×2-1+
1×2-2,或用十進制表示為16+4+2+0.5+0.25=22.75。
為了區分十進制數、二進制數和十六進制數,我們分别用下标10、2和16表示基數(例如123410、10100112和12a316)。不過,若一個數的基數是顯而易見的,則可以将下标省略掉。
計算機科學家對4種數制感興趣:十進制、二進制、八進制和十六進制(十六進制通常被縮寫為hex)。八進制數現在使用不多,是以本書不再讨論。表2-2列出了每種數制所使用的數字。由于十六進制數有16個數字,字母a~f分别表示數值10~15。例如,12cf16包括數字1、2、12和15。人們用十六進制數表示位數很多的二進制數。例如,8位二進制數10001001等于十六進制數89,後者更容易記。