本期問題在2000年以前非常有名……
阿凡提收獲了1000斤蘿蔔,自己吃吃不完,要賣就要去大集市。但因為阿凡提離群索居,住的地方很偏僻。要去城裡需要穿越100裡的沙漠瀚海。
已知阿凡提的驢子最大載重就是100斤,同時在沙漠裡每走1裡地,就需要吃掉1斤蘿蔔。阿凡提需要自帶吃喝盤纏,是以不能幫驢子分擔負重。顯而易見,阿凡提無法一次性地把蘿蔔帶到集市,但是他可以采取下面的政策。
阿凡提事先帶着驢子把部分蘿蔔埋藏在他沿路的秘密地點,作為補給。當然,這樣來回往返,也會消耗很多蘿蔔。但是因為阿凡提親手種的蘿蔔可以增加智力屬性,是以每根價格都相當于800年的老參——隻要送到市場上,哪怕就一根收益也很大。
現在問,阿凡提總共可以在集市裡賣出多少斤蘿蔔?(注意要往返哦)
網上流傳的國中幾何題目
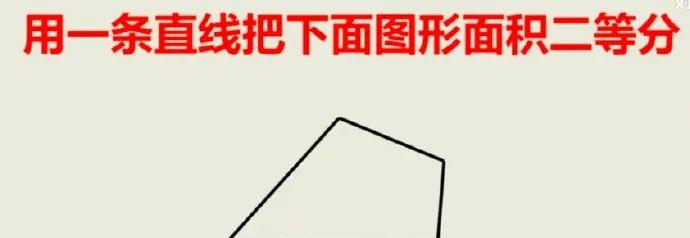
首先一點,認為經過質心的直線可以平分面積的想法是錯的。
用 ID 為 ≠0 的解釋
過質心等分的各位,試一試等邊三角形質心平行于一邊的直線?質心是力矩平衡,相當于每個點以其到直線的距離加了權,而算面積的時候所有點的權均為 1。
比如說,等邊三角形,過幾何中心且與一邊平行,則把原始三角形分成上面的小三角形和下面的梯形。小三角形和原三角形相似,相似比是2:3。則面積的比是4:9。顯然,這條線沒有平分原圖像的面積。
正解
在四邊形ABCD中,取對角線BD的中點O,連接配接OA、OC.顯然,折線段AO-OC能平分四邊形ABCD的面積,再過點O作OE∥AC交CD于E,則直線AE即為所求。
證明:
因為OE∥AC,
是以S△AOE=S△COE,
是以S△AOF=S△CEF,
又因為,折線AOC能平分四邊形ABCD的面積,
是以直線AE平分四邊形ABCD的面積
另一隻雞:
四邊形ABCD。過AC中點O做BD的平行線,交AB或BC于P。直線PD平分四邊形ABCD。證明:由于O是AC中點,不難發現三角形AOB和三角形AOD面積占了四邊形ABCD的一半。又由于OP平行于BD,是以三角形OPD面積等于三角形OPB的面積。四邊形ABPD(或者三角形APD)面積等于三角形AOB+三角形AOD-三角形OPB+三角形OPD,即四邊形ABCD的一半。
翅痕
設順時針四個頂點為ABCD,連接配接其中一個對角線AC,過B點做AC的平行線,那麼在這條平行線上任意移動B點不會變化三角形ABC的面積,将這條平行線與DC延長線相交與E,那麼就變成了平分三角形AED的問題,找出DE的中心點F,需要F落在CD之間,連接配接AF即平分了面積。
另外,nerv同學提到
這題讓我想到之前上大學的時候想到的一個問題:對于任意鹵蛋,是否都存在一個方法能一刀同時等分蛋清和蛋黃。每次去買肉夾馍吃的時候都會想一會,困擾了我好幾年。
搜尋“三明治定理”,就能解惑。