4.6 梯度消失與梯度爆炸
4.6.1 梯度消失
根據上文BP算法中的推導,我們從公式4.44,4.45,4.46中可以知道,權值的調整ΔW是跟學習信号δ相關的。同時我們從4.41,4.42,4.43中可以知道在學習信号δ表達式中存在f ’ (x)。也就是說激活函數的導數會影響學習信号δ的值,而學習信号δ的值會影響權值調整ΔW的值。那麼激活函數的值越大,ΔW的值就越大;激活函數的值越小,ΔW的值也就越小。
假設激活函數為sigmoid函數,前文中我們已經知道了sigmoid函數的表達式為: f ( x ) = 1 1 + e − x f(x)=\frac{1}{1+e^{-x}} f(x)=1+e−x1,sigmoid函數的導數為: f ′ ( x ) = f ( x ) [ 1 − f ( x ) ] f ' (x) = f(x)[1-f(x)] f′(x)=f(x)[1−f(x)],我們可以畫出sigmoid函數的導數圖像為圖4.18:
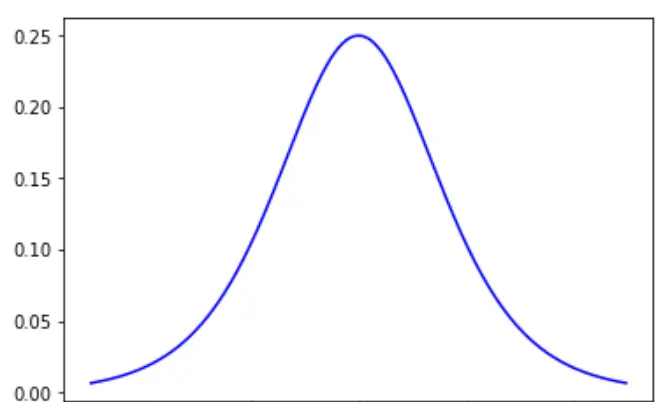
這裡我們發現當x=0時,sigmoid函數導數可以取得最大值0.25。x取值較大或較小時,sigmoid函數的導數很快就趨向于0。不管怎麼樣,sigmoid函數的導數都是一個小于1的數,學習信号δ乘以一個小于1的數,那麼δ就會減小。學習信号從輸出層一層一層向前反向傳播的時候,每傳播一層學習信号就會變小一點,經過多層傳播後,學習信号就會接近于0,進而使得權值ΔW調整接近于0。ΔW接近于0那就意味着該層的參數不會發生改變,不能進行優化。參數不能優化,那整個網絡就不能再進行學習了。學習信号随着網絡傳播逐漸減小的問題也被稱為**梯度消失(vanishing gradient)**的問題。
我們再考慮一下tanh函數的導數,tanh函數的表達式為: f ( x ) = e x − e − x e x + e − x f(x)=\frac{e^x-e^{-x}}{e^x+e^{-x}} f(x)=ex+e−xex−e−x,tanh函數的導數為: f ′ ( x ) = 1 − ( f ( x ) ) 2 f ' (x) = 1- (f(x))^2 f′(x)=1−(f(x))2 ,tanh函數的導數如圖4.19:
t a n h tanh tanh函數導數圖像看起來比sigmoid函數要好一些,x=0時, t a n h tanh tanh函數導數可以取得最大值1。x取值較大或較小時, t a n h tanh tanh函數的導數很快就趨向于0。不管怎麼樣, t a n h tanh tanh函數導數的取值總是小于1的,是以tanh作為激活函數也會存在梯度消失的問題。
對于softsign函數,softsign函數的表達式為: f ( x ) = x 1 + ∣ x ∣ f(x)=\frac{x}{1+|x|} f(x)=1+∣x∣x,softsign函數的導數為: f ′ ( x ) = 1 ( 1 + ∣ x ∣ ) 2 f '(x)=\frac{1}{(1+|x|)^2} f′(x)=(1+∣x∣)21,softsign函數的導數如圖4.20:
softsign函數x=0時,softsign函數導數可以取得最大值1。x取值較大或較小時,softsign函數的導數很快就趨向于0。不管怎麼樣,softsign函數導數的取值總是小于1的,是以softsign作為激活函數也會存在梯度消失的問題。
4.6.2 梯度爆炸
當我們使用sigmoid,tanh和softsign作為激活函數時,它們的導數取值範圍都是小于等于1的,是以會産生梯度消失的問題。那麼我們可能會想到,如果使用導數大于1的函數作為激活函數,情況會如何?
如果學習信号δ乘以一個大于1的數,那麼δ就會變大。學習信号從輸出層一層一層向前反向傳播的時候,每傳播一層學習信号就會變大一點,經過多層傳播後,學習信号就會接近于無窮大,進而使得權值ΔW調整接近于無窮大。ΔW接近于無窮大那就意味着該層的參數,處于一種極不穩定的狀态,那麼網絡就不能正常工作了。學習信号随着網絡傳播逐漸增大的問題也被稱為**梯度爆炸(exploding gradient)**的問題。
4.6.3 使用ReLU函數解決梯度消失和梯度爆炸的問題
我們知道ReLU的表達式為:f(x) = max(0,x)。當x小于0時,f(x)的取值為0;當x大于0時,f(x)的取值等于x。ReLU函數的導數如圖4.21:
前面我們讨論了當激活函數的導數小于1時,網絡會産生梯度消失,激活函數的導數大于1時,網絡會産生梯度爆炸。那麼當我們使用ReLU作為激活函數的時候,x小于0時,ReLU的導數為0;x大于0時,ReLU的導數為1。導數為1是一個很好的特性,不會使得學習信号越來越小,也不會讓學習信号越來越大,可以讓學習信号比較穩定地從後向前傳播。解決了梯度消失和梯度爆炸的問題,同時計算友善,可以加速網絡的訓練。
ReLU也存在缺點,由于x小于0的部分f(x)的取值恒定為0,會導緻一些神經元無法激活。
不過總的來說,ReLU還是優點大于缺點的,是以在一些比較深層的神經網絡中,通常都會使用ReLU作為神經網絡的激活函數。
除此之外可能我們還會想到線性激活函數y = x 的導數也是等于1,也可以克服梯度消失和梯度爆炸的問題。不過之前我們也多次提到線性激活函數不會能描繪非線性的分類邊界,是以無法處理非線性問題。是以線性函數依舊不算是一個好的激活函數。