pcl把3dmesh 映射成2維_SVM與SVR（2）——SVM、SVM柔性邊界和核函數

* 以下内容是在學習過程中的一些筆記，難免會有錯誤和纰漏的地方。如果造成任何困擾，很抱歉。 *

限于篇幅過長，分為三個部分：

1.SVM與SVR（1）——KKT條件和Lagrange對偶函數g

2.SVM與SVR（2）——SVM、SVM柔性邊界和核函數

3.SVM與SVR（3）——SVR和SVR、SVM的support vector對比

開始正文。

2.1 SVM（支援向量機， Support Vector Machines）

2.11 超平面（Hyperplane）

回到第一篇最開始給出的第一個例子（例1）：

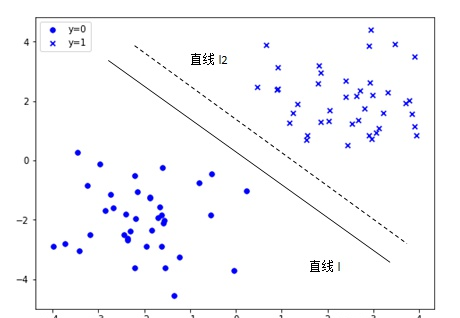
在如上圖的二維空間裡，有兩類不同個體（y=0和y=1），我們友善讨論就說C0類（y=0）和C1類（y=1）。。很明顯，在“中間”畫一條直線l，就可以判斷一個樣本的所屬類别（直線l上方為C1，直線下方為C0）。

那麼如果在三維空間裡呢？可以找到z=0（或z=0.25）的一個平面，把C0和C1區分出來：位于z=0平面上方為C1，位于z=0平面下方為C2。

更一般地，在n維線性空間，我們嘗試找到一個

超平面（Hyperplane）

。有了這個超平面，我們就可以判斷某個樣本屬于C0還是C1了。在二維空間裡面，超平面就是一條線；在三維空間裡，超平面就是一個面；...；在n維線性空間裡，超平面應該是（n-1）次元的。

我們設超平面的表達式為

。其中，

和

為n*1維列向量。

即，我們在意的是

，其中

表示判斷符号函數。

2.12 幾何間隔（Geometric Margin）

我們現在已經确定要找一個超平面（Hyperplane）。再回到最初的例1：會發現，直線l和直線2在這個圖中都可以作為我們想到的直線，如果隻是單純看起來區分C0和C1。或者說，這個例子中，其實能找出來無數條直線。那這無數條直線中，有沒有所謂的好壞呢？如果有好壞，怎麼樣找到那條最好的？

這個好壞的标準就是：

幾何間隔（Geometric Margin）

。

我們設一個樣本為

，其中

為

維列向量（可以了解成一個個體有n個特征（features）），

等于-1或者1。

定義，

。如果把

和

歸一化，用

和

表示，則有：

。其中，

為向量

的範數,它的p-範數為

。我們一般用2-範數。

當用2-範數時，

即為“幾何間距”，點到超平面的距離。我們一般設

。其中，

表示離超平面最近的點。這裡

設成1，我了解：設成幾都可以，無非就是前面的

和

同時放縮一下。就像下圖，

設成幾，無非就是所有的點到直線的距離擴大縮小而已。更嚴謹的證明見：為什麼SVM推導過程中，可以令幾何間隔等于1？

為什麼幾何間隔越大，越好？

因為幾何間隔與誤分次數有如下關系：誤分次數

。其中，

，即樣本中向量長度最長的值（樣本分布最遠）。

通過上式可知，

越大，誤分次數上界越小。是以，所謂的“最好” =

形象的也很友善。如下圖，Fig 1是一個幾何間隔大的超平面，Fig 2是一個幾何間隔小的超平面。實線代表超平面H（不應該用射線...），Fig 1的應該是更好的。因為在Fig 2中，超平面H離圓圈類别太近了。很容易就把圓圈類别誤判成方塊。

Fig 1 Fig 2

綜上所述，我們要找的超平面，最大化幾何間隔（

）是最好的。

上述幾何問題就變成了一個最優化的代數問題：

另外，上述過程我們設

。其中，

表示離超平面最近的點。即所有樣本點間隔

。

最開始的問題

2.2 SVM柔性邊界

現實中，有很多問題并不是像例1圖中那麼“完全可分”。如下圖，因為極個别樣本（樣本A）,導緻無解（找不到一個超平面可以完全區分C0和C1）。又或者找一條非常彎曲的曲線用來高精度地區分C0和C1，不過其實這就犯了過度拟合的錯誤。用這種方法，在高次元中，因為一些極端值，需要頻繁地彎曲超平面。

其實上圖中，除了A點，其他點就可以被直線分類了。是以，我們可能會認為點A是個極端點，可以忽略這類點。是以，為了引入容錯性，給式子（1）的硬性門檻值（1）加一個“

松弛變量

”。

在2.1中公式變成如下形式：

式子中的

的出現，即允許出現間隔比1小的點，而且我們放棄了對這類點的精确分類。換回來的，我們不必因為極端點頻繁地移動，可以得到更大的幾何間隔。

式子中的

C被稱為懲罰因子。

可以從以下幾個角度了解它。

如果考慮所有點，那麼在極端值附近，波動會很大（，突然地跳躍，出現過拟合現象）。因為有了

這項的存在，在一個求最小值的過程中，相當于對它的懲罰（損失）。

的大小說明了對于離群點的在意程度。C越大，說明這個離群點損失就越大，即越不願意放棄這個點。

C是一個使用者指定的系數。

其實SVM柔性邊界的存在，就像個别（離散）點和更大幾何間隔（分類邊界更平衡）的一個trade off。

從幾何角度了解一下柔性邊界做了一個什麼工作：

完美可分 柔性邊界

在完美可分的情況下，帶狀區域就是兩倍的幾何間距，柔性邊界呢就是把這個距離放大了，本來這個帶狀區域中沒有訓練樣本，現在我允許可以有一些訓練樣本了，不等式中的1就是縮放後的帶狀區間的邊界，現在訓練樣本滿足的公式可以比這個邊界小了，自然就是允許一部分訓練樣本點在帶狀區域裡面了。

回到式子（2），發現它符合KKT條件，拉格朗日乘子式即為：

KKT條件可得：

。當

等于0時，相當于限制條件無效，即點i是邊界外的非異常點。對求解超平面H，無影響；當

大于0的時候，限制條件有效。

它的幾何意義就是說，樣本點（Observations）可能會很多，但真正對H确定有影響的可能就那麼幾個點：在完全可分情況下，為H1,H2上的點；在柔性邊界的情況下，為H1和H2區域内的點（反方向太多，也允許超過區域，例如圖中點5）。這些點也被稱為

支援向量（Support Vector）

。SVM也就可以了解成其實就是在找“支援向量（Support Vector）”。少數的支援向量确定了SVM 的最終決策函數，計算的複雜性取決于支援向量，而不是整個樣本空間，這就可以避免“維數災難”。

完全可分，虛線上的點為支援向量 柔性邊界下的支援向量

2.3 完美可分情況下的SVM求解：

柔性邊界情況下的解法，跟第三篇中的SVR解法很像。這裡僅以完美可分SVM為例：

上式的dual question為：

第一個等式展開即為：

。其中

了解為個體i的第f個特征（features）。将式子（5）帶回（4），求得：

解出

後，求出

即可得到模型:

2.4 核函數（ kernel function ）

回到這個圖上，如果單純在二維（x, y）想找到一個線性函數對C0和C1分類是非常困難的。但在三維空間，找一個超平面就會非常容易區分C0和C1。

是以，樣本在原始樣本空間是不可分的，可以嘗試映射到更高次元，那可能就可以線性區分C0和C1了。幸運的是，有如下結論：如果原始空間是有限維，即屬性數有限，那麼一定存在一個高維特征空間使樣本可分。令

表示将x映射後的特征向量，那麼在新次元空間中，超平面即為：

。2.3中求得的對偶問題中就包含

。因為這涉及到了更高次元的内積，次元很高的時候計算該值可能就比較困難。但是我們最終目的是求一個内積。如果有一個函數可以保證

， 那就可以在原始次元計算出來（高緯度）內積。這個

就是核函數（kernel function）

。