pcl把3dmesh 映射成2维_SVM与SVR（2）——SVM、SVM柔性边界和核函数

* 以下内容是在学习过程中的一些笔记，难免会有错误和纰漏的地方。如果造成任何困扰，很抱歉。 *

限于篇幅过长，分为三个部分：

1.SVM与SVR（1）——KKT条件和Lagrange对偶函数g

2.SVM与SVR（2）——SVM、SVM柔性边界和核函数

3.SVM与SVR（3）——SVR和SVR、SVM的support vector对比

开始正文。

2.1 SVM（支持向量机， Support Vector Machines）

2.11 超平面（Hyperplane）

回到第一篇最开始给出的第一个例子（例1）：

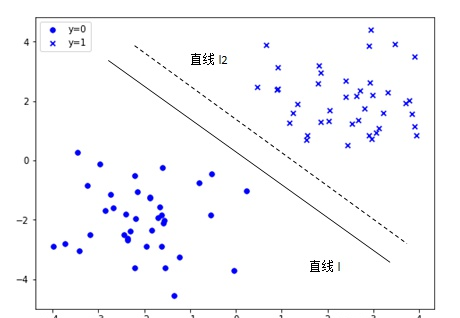
在如上图的二维空间里，有两类不同个体（y=0和y=1），我们方便讨论就说C0类（y=0）和C1类（y=1）。。很明显，在“中间”画一条直线l，就可以判断一个样本的所属类别（直线l上方为C1，直线下方为C0）。

那么如果在三维空间里呢？可以找到z=0（或z=0.25）的一个平面，把C0和C1区分出来：位于z=0平面上方为C1，位于z=0平面下方为C2。

更一般地，在n维线性空间，我们尝试找到一个

超平面（Hyperplane）

。有了这个超平面，我们就可以判断某个样本属于C0还是C1了。在二维空间里面，超平面就是一条线；在三维空间里，超平面就是一个面；...；在n维线性空间里，超平面应该是（n-1）维度的。

我们设超平面的表达式为

。其中，

和

为n*1维列向量。

即，我们在意的是

，其中

表示判断符号函数。

2.12 几何间隔（Geometric Margin）

我们现在已经确定要找一个超平面（Hyperplane）。再回到最初的例1：会发现，直线l和直线2在这个图中都可以作为我们想到的直线，如果只是单纯看起来区分C0和C1。或者说，这个例子中，其实能找出来无数条直线。那这无数条直线中，有没有所谓的好坏呢？如果有好坏，怎么样找到那条最好的？

这个好坏的标准就是：

几何间隔（Geometric Margin）

。

我们设一个样本为

，其中

为

维列向量（可以理解成一个个体有n个特征（features）），

等于-1或者1。

定义，

。如果把

和

归一化，用

和

表示，则有：

。其中，

为向量

的范数,它的p-范数为

。我们一般用2-范数。

当用2-范数时，

即为“几何间距”，点到超平面的距离。我们一般设

。其中，

表示离超平面最近的点。这里

设成1，我理解：设成几都可以，无非就是前面的

和

同时放缩一下。就像下图，

设成几，无非就是所有的点到直线的距离扩大缩小而已。更严谨的证明见：为什么SVM推导过程中，可以令几何间隔等于1？

为什么几何间隔越大，越好？

因为几何间隔与误分次数有如下关系：误分次数

。其中，

，即样本中向量长度最长的值（样本分布最远）。

通过上式可知，

越大，误分次数上界越小。所以，所谓的“最好” =

形象的也很方便。如下图，Fig 1是一个几何间隔大的超平面，Fig 2是一个几何间隔小的超平面。实线代表超平面H（不应该用射线...），Fig 1的应该是更好的。因为在Fig 2中，超平面H离圆圈类别太近了。很容易就把圆圈类别误判成方块。

Fig 1 Fig 2

综上所述，我们要找的超平面，最大化几何间隔（

）是最好的。

上述几何问题就变成了一个最优化的代数问题：

另外，上述过程我们设

。其中，

表示离超平面最近的点。即所有样本点间隔

。

最开始的问题

2.2 SVM柔性边界

现实中，有很多问题并不是像例1图中那么“完全可分”。如下图，因为极个别样本（样本A）,导致无解（找不到一个超平面可以完全区分C0和C1）。又或者找一条非常弯曲的曲线用来高精度地区分C0和C1，不过其实这就犯了过度拟合的错误。用这种方法，在高维度中，因为一些极端值，需要频繁地弯曲超平面。

其实上图中，除了A点，其他点就可以被直线分类了。所以，我们可能会认为点A是个极端点，可以忽略这类点。所以，为了引入容错性，给式子（1）的硬性阈值（1）加一个“

松弛变量

”。

在2.1中公式变成如下形式：

式子中的

的出现，即允许出现间隔比1小的点，而且我们放弃了对这类点的精确分类。换回来的，我们不必因为极端点频繁地移动，可以得到更大的几何间隔。

式子中的

C被称为惩罚因子。

可以从以下几个角度理解它。

如果考虑所有点，那么在极端值附近，波动会很大（，突然地跳跃，出现过拟合现象）。因为有了

这项的存在，在一个求最小值的过程中，相当于对它的惩罚（损失）。

的大小说明了对于离群点的在意程度。C越大，说明这个离群点损失就越大，即越不愿意放弃这个点。

C是一个用户指定的系数。

其实SVM柔性边界的存在，就像个别（离散）点和更大几何间隔（分类边界更平衡）的一个trade off。

从几何角度理解一下柔性边界做了一个什么工作：

完美可分 柔性边界

在完美可分的情况下，带状区域就是两倍的几何间距，柔性边界呢就是把这个距离放大了，本来这个带状区域中没有训练样本，现在我允许可以有一些训练样本了，不等式中的1就是缩放后的带状区间的边界，现在训练样本满足的公式可以比这个边界小了，自然就是允许一部分训练样本点在带状区域里面了。

回到式子（2），发现它符合KKT条件，拉格朗日乘子式即为：

KKT条件可得：

。当

等于0时，相当于限制条件无效，即点i是边界外的非异常点。对求解超平面H，无影响；当

大于0的时候，限制条件有效。

它的几何意义就是说，样本点（Observations）可能会很多，但真正对H确定有影响的可能就那么几个点：在完全可分情况下，为H1,H2上的点；在柔性边界的情况下，为H1和H2区域内的点（反方向太多，也允许超过区域，例如图中点5）。这些点也被称为

支持向量（Support Vector）

。SVM也就可以理解成其实就是在找“支持向量（Support Vector）”。少数的支持向量确定了SVM 的最终决策函数，计算的复杂性取决于支持向量，而不是整个样本空间，这就可以避免“维数灾难”。

完全可分，虚线上的点为支持向量 柔性边界下的支持向量

2.3 完美可分情况下的SVM求解：

柔性边界情况下的解法，跟第三篇中的SVR解法很像。这里仅以完美可分SVM为例：

上式的dual question为：

第一个等式展开即为：

。其中

理解为个体i的第f个特征（features）。将式子（5）带回（4），求得：

解出

后，求出

即可得到模型:

2.4 核函数（ kernel function ）

回到这个图上，如果单纯在二维（x, y）想找到一个线性函数对C0和C1分类是非常困难的。但在三维空间，找一个超平面就会非常容易区分C0和C1。

所以，样本在原始样本空间是不可分的，可以尝试映射到更高维度，那可能就可以线性区分C0和C1了。幸运的是，有如下结论：如果原始空间是有限维，即属性数有限，那么一定存在一个高维特征空间使样本可分。令

表示将x映射后的特征向量，那么在新维度空间中，超平面即为：

。2.3中求得的对偶问题中就包含

。因为这涉及到了更高维度的内积，维度很高的时候计算该值可能就比较困难。但是我们最终目的是求一个内积。如果有一个函数可以保证

， 那就可以在原始维度计算出来（高纬度）內积。这个

就是核函数（kernel function）

。