數學模組化常見的一些方法【02TOPSIS/優劣解距離法】

@

目錄

• 數學模組化常見的一些方法
  • TOPSIS法
    • TOPSIS的介紹
    • 優劣解距離法操作步驟
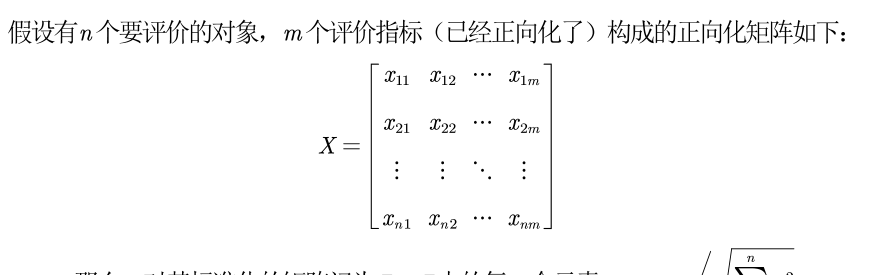
      • 1. 将原始矩陣正向化
        • 1.1 極小型名額 → 極大型名額
        • 1.2 中間型名額 → 極大型名額
        • 1.3 區間型名額 → 極大型名額
      • 2. 正向化矩陣标準化
      • 3. 計算得分并歸一化
    • 标準化處理公式
    • 類比隻有一個名額計算得分

（Technique for Order Preference by Similarity to Ideal Solution）

• 可翻譯為逼近理想解排序法，國内常簡稱為優劣解距離法
• TOPSIS 法是一種常用的綜合評價方法，其能充分利用原始資料的資訊，其結果能精确地反映各評價方案之間的差距。

C.L.Hwang 和 K.Yoon 于1981年首次提出 TOPSIS (Technique forOrder Preference by Similarity to an Ideal Solution)，可翻譯為逼近理想解排序法，國内常簡稱為優劣解距離法.。

  TOPSIS 法是一種常用的綜合評價方法，能充分利用原始資料的資訊，其結果能精确地反映各評價方案之間的差距。

  基本過程為先将原始資料矩陣統一名額類型（一般正向化處理）得到正向化的矩陣，再對正向化的矩陣進行标準化處理以消除各名額量綱的影響，并找到有限方案中的最優方案和最劣方案，然後分别計算各評價對象與最優方案和最劣方案間的距離，獲得各評價對象與最優方案的相對接近程度，以此作為評價優劣的依據。該方法對資料分布及樣本含量沒有嚴格限制，資料計算簡單易行。

名額名稱	名額特	例子
極大型（效益型）名額	越大（多）越好	成績、GDP增速、企業利潤
極小型（成本型）名額	越小（少）越好	費用、壞品率、污染程度
中間型名額	越接近某個值越好	水品質評估時的PH值
區間型名額	落在某個區間最好	體溫、水中植物性營養物量

• 所謂的将原始矩陣正向化，就是要将所有的名額類型統一轉化為極大型名額。

具體計算過程看後部分

計算代碼:

>> X = [89,1;60,3;74,2;99,0]
>> [n,m]=size(X)
>> X ./ repmat(sum(X .* X) .^0.5, n,1)
           

計算過程：

>> X = [89,1;60,3;74,2;99,0]
X =
    89     1
    60     3
    74     2
    99     0

>> [n,m]=size(X)
n = 4
m = 2

>> sum(X .* X)
ans = 26798   14

>> sum(X .* X) .^0.5
ans = 163.7009  3.7417

>> repmat(sum(X .* X) .^0.5, n,1)
ans =
  163.7009    3.7417
  163.7009    3.7417
  163.7009    3.7417
  163.7009    3.7417

>> X ./ repmat(sum(X .* X) .^0.5, n,1)
ans =
    0.5437    0.2673
    0.3665    0.8018
    0.4520    0.5345
    0.6048         0
           

>> X = [89,1;60,3;74,2;99,0]
>> [n,m]=size(X)
>> Z = X ./ repmat(sum(X .* X) .^0.5, n,1)
>> D_P = sum([(Z - repmat(max(Z),n,1)).^2 ],2) .^ 0.5 %D+向量
>> D_N = sum([(Z - repmat(min(Z),n,1)).^2 ],2) .^ 0.5 %D-向量
>> A = D_N ./ (D_P + D_N) % 未歸一化的得分
>> A ./ repmat(sum(A),n,1) % 歸一化的得分
           

>> max(Z)
ans = 0.6048    0.8018

>> min(Z)
ans = 0.3665         0

>> repmat(max(Z),n,1)
ans =
    0.6048    0.8018
    0.6048    0.8018
    0.6048    0.8018
    0.6048    0.8018

>> repmat(min(Z),n,1)
ans =
    0.3665         0
    0.3665         0
    0.3665         0
    0.3665         0

>> (Z - repmat(max(Z),n,1)).^2
ans =
    0.0037    0.2857
    0.0568         0
    0.0233    0.0714
         0    0.6429

>> (Z - repmat(min(Z),n,1)).^2
ans =
    0.0314    0.0714
         0    0.6429
    0.0073    0.2857
    0.0568         0

>> sum([(Z - repmat(max(Z),n,1)).^2 ],2)
ans =
    0.2894
    0.0568
    0.0948
    0.6429

>> sum([(Z - repmat(min(Z),n,1)).^2 ],2)
ans =
    0.1028
    0.6429
    0.2930
    0.0568

>> D_P = sum([(Z - repmat(max(Z),n,1)).^2 ],2) .^ 0.5
D_P =
    0.5380
    0.2382
    0.3078
    0.8018

>> D_N = sum([(Z - repmat(min(Z),n,1)).^2 ],2) .^ 0.5
D_N =
    0.3206
    0.8018
    0.5413
    0.2382

>> A = D_N ./ (D_P + D_N) % 未歸一化的得分
A =
    0.3734
    0.7709
    0.6375
    0.2291

>> A ./ repmat(sum(A),n,1) % 歸一化的得分
ans =
    0.1857
    0.3834
    0.3170
    0.1139
           

參考連結