Adversarial Training with Rectified Rejection

目录

概

主要内容

rejection

实际使用

代码

Pang T., Zhang H., He D., Dong Y., Su H., Chen W., Zhu J., Liu T. Adversarial training with rectified rejection. arXiv Preprint, arXiv: 2105.14785, 2021.

通过对置信度进行矫正, 然后再根据threshold (1/2)判断是否拒绝. 有点detection的味道, 总体来说是很有趣的点子.

假设一个网络\(f_{\theta}\) 将样本\(x\)映射为概率向量\(f_{\theta}(x)\), 则其置信度(confidence)为

\[f_{\theta}(x)[y^m], y^m := \mathop{\arg\max} \limits_{k} f_{\theta}(x)[k],

\]

若该样本的真实的标签为\(y\), 进一步定义真实的置信度\(\text{T-Con}\)为

\[f_{\theta}(x)[y].

我们进一步定义一个分类器\(F\):

\[F(x) =

\left \{

\begin{array}{ll}

y^m & \text{if } f_{\theta}(x)[y] \ge \frac{1}{2}, \\

\text{don't know} & \text{if } f_{\theta}(x)[y] < \frac{1}{2}.

\end{array}

\right .

显然这种情况下, 就算\(f\)训练得再糟糕, \(F\)都不会分错(虽然可能大部分都是拒绝判断, 但是拒绝判断在面对对抗样本的时候是有用的).

但是上面的情况是必须知道样本标签\(y\)的, 都知道标签了还弄个分类器不是多次一举. 所以我们现在要做的, 是做一个近似

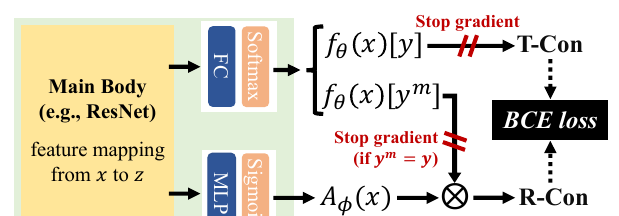
如上图所示, 我们要通过一个近似的\(\text{R-Con}\)来代替\(\text{T-Con}\), Rectified Confidence通过如下的方式构建:

通过encoder将\(x\)映为特征\(z\);

\(z\)通过全连接层和softmax层获得概率向量\(f_{\theta}(x)\);

\(z\)通过MLP和sigmoid层获得\(A_{\phi}(x) \in [0, 1]\);

计算Rectified Confidence:

\[\text{R-Con}(x) = f_{\theta}(x)[y^m]A_{\phi}(x).

显然, 若要\(\text{R-Con}(x) = \text{T-Con}(x)\), 则有

\[A_{\phi}(x) = A_{\phi}^*(x) = \frac{f_{\theta}(x)[y]}{f_{\theta}(x)[y^m]}.

为此, 通过BCE损失:

\[\mathcal{L}_{RR}(x, y;\theta, \phi)

= \mathbf{BCE}(f_{\theta}(x)[y^m]A_{\phi}(x) \| f_{\theta}(x)[y]) \\

\mathbf{BCE}(f\|g) = g \cdot \log f + (1 - g) \cdot \log (1 - f).

故总的损失为:

\[\min_{\theta, \phi}\: \mathbb{E}_{p(x y)}[\mathcal{L}_T(x^*, y;\theta) + \lambda \mathcal{L}_{RR}(x^*, y; \theta, \phi)], \\

x^* = \mathop{\arg \max} \limits_{x' \in B(x)} \mathcal{L}_{A}(x', y; \theta).

注意图中的stop gradient部分, 最上面是为了一个单向的趋近(虽然encoder部分是会依然交涉), 第二个部分作者觉得当\(y^m = y\)时, 该样本比较简单, 而对抗学习应该注中难的样本, 这样不容易陷入局部最优, 经验之谈吧.

y^m & \text{if } \text{R-Con}(x) \ge \frac{1}{2}, \\

\text{don't know} & \text{if } \text{R-Con}(x) < \frac{1}{2}.

现在的疑问是, 什么时候这个分类器是没有错判的.

定义: 当下列界,

\(|\log (\frac{A_{\phi}(x)}{A_{\phi}^*(x)})| \le \log (\frac{2}{2-\xi})\);

\(|A_{\phi}(x) - A_{\phi}^*(x)| \le \frac{\xi}{2}\)

至少一个成立时, 称\(A_{\phi}(x)\)在点\(x\)处为\(\xi\text{-error}\), \(\xi \in [0, 1)\).

定理1: 假设\(x_+, x_-\)分别为被\(f\)正判和误判的样本, 即

\[y_+^m = y_+, y^m_- \not = y_-,

但均满足(即置信度足够高)

\[f(x_+)[y_+^m] > \frac{1}{2-\xi}, \quad f(x_-)[y_-^m] > \frac{1}{2-\xi}, \: \xi \in [0, 1).

若\(A_{\phi}\)在\(x_+, x_-\)处满足\(\xi\text{-error}\), 则\(\text{R-Con}(x_+) > \frac{1}{2} > \text{R-Con}(x_-)\), 即此时\(F(x_+)\)为正确判断, \(F(x_-)\)拒绝判断.

proof:

界1等价于:

\[\frac{2-\xi}{2}f(x)[y] \le \text{R-Con}(x) \le \frac{2}{2-\xi} f(x)[y],

界2等价于

\[f(x)[y] - \frac{\xi}{2} f(x)[y^m] \le \text{R-Con}(x) \le f(x)[y] + \frac{\xi}{2} f(x)[y^m].

因为

\[f(x_+)[y_+] = f(x_+)[y_+^m] > \frac{1}{2 - \xi},\\

\frac{2-\xi}{2}f(x_+)[y_+] > \frac{1}{2}, \\

f(x)[y] - \frac{\xi}{2} f(x)[y^m] = f(x)[y^m] - \frac{\xi}{2} f(x)[y^m] > \frac{1}{2}.

所以\(\text{R-Con}(x_+) > \frac{1}{2}\).

又因为

\[f(x)[y] \le 1 - f(x)[y^m] \Rightarrow f(x_-)[y_-] < \frac{1-\xi}{2-\xi}.

易证

\[\frac{2}{2-\xi}\frac{1-\xi}{2-\xi} \le \frac{1}{2}, \xi \in [0, 1),

\[f(x_-)[y_-] + \frac{\xi}{2}f(x_-)[y^m_-] \le 1 - t + \frac{\xi}{2}t < \frac{1}{2}, \quad t:= f(x_-)[y_-^m] > \frac{1}{2-\xi}.

故\(\text{R-Con}(x_-) < \frac{1}{2}\).

证毕.

在实际使用中, threshold 似乎并不是固定为1/2, 而是通过TPR-FPR曲线选择的(TPR-95).

y^m & \text{if } \text{R-Con}(x) \ge t, \\

\text{don't know} & \text{if } \text{R-Con}(x) < t.

原文代码