Yesterday we derived Taylor's formula, and today we will continue to look at some of the other formulas that he elicited.
<h1 class="pgc-h-arrow-right" data-track="2" > Peiano remainder</h1>
Sometimes, in order to make it easier to calculate and represent, when we do not need to express it precisely, we express the remainder as the form of some infinitesimally small product, which is the expression of the Peiano coherent:
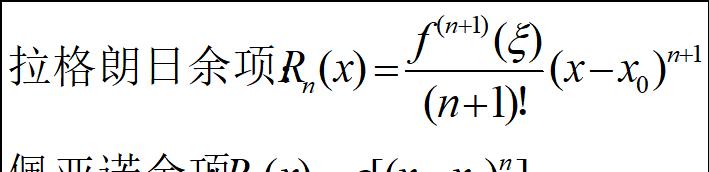
Peiano remainder
The corresponding nth-order Taylor formula with Peyano's remainder is:
N-order Taylor formula with Peiano's remainder
Since the n+1 derivative of f(x) is not required in the Peiano polylogy, it is true as long as f(x) is at point x0 until the nth order derivative is sufficient. The proof is as follows
Peiano's remainder reasoning process
<h1 class="pgc-h-arrow-right" data-track="11" > special value of Taylor's formula</h1>
When n=0, Taylor's formula becomes Lagrange's median theorem
Lagrange's median theorem
When n=1, Taylor's formula becomes:
Taylor's formula for n=1
F(x) can be approximated using the above formula:
Approximate calculation of f(x).
<h1 class="pgc-h-arrow-right" data-track="22" > McLaughlin's formula</h1>
In Taylor's formula we take x0=0, then there is McLaughlin's formula:
McLaughlin's formula
For McLaughlin can get an approximate formula for the function:
Approximate calculation of the function
For its error there is the following inequality holds:
The error of McLaughlin's formula
<h1 class="pgc-h-arrow-right" data-track="30" > five important commonly used McLaughlin formulas</h1>
Taylor expandable for commonly used functions
<h1 class="pgc-h-arrow-right" data-track="33" > a few points</h1>
The Taylor formula for the function at the same point is unique
Taylor's formula with Peyano's remainder mainly describes the functional properties of x in the x0 attachment
Taylor's formula with lagrangian remainder mainly describes the properties of x in the open interval (a,b).
To be continued...