昨天我们推导出泰勒公式,今天我们再继续看看由他引出的其他一些公式。
<h1 class="pgc-h-arrow-right" data-track="2">佩亚诺余项</h1>
有的时候为了计算和表示更方便,在不需要精确表达的时候我们把余项表达为某个无穷小乘积的形式,这就是佩亚诺余项的表达方式:
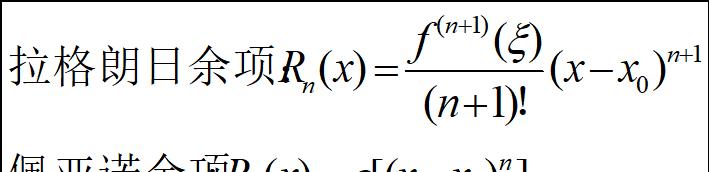
佩亚诺余项
相应的带佩亚诺余项的n阶泰勒公式为:
带佩亚诺余项的n阶泰勒公式
由于佩亚诺余项中不需要f(x)的n+1阶导数,因此只要f(x)在点x0直到n阶可导上式就可以成立。证明如下
佩亚诺余项推理过程
<h1 class="pgc-h-arrow-right" data-track="11">泰勒公式特殊取值</h1>
当n=0时,泰勒公式变为拉格朗日中值定理
拉格朗日中值定理
当n=1时,泰勒公式变成:
n=1的泰勒公式
可以用上面的公式近似计算f(x):
f(x)的近似计算
<h1 class="pgc-h-arrow-right" data-track="22">麦克劳林公式</h1>
在泰勒公式中我们取x0=0,则有麦克劳林公式:
麦克劳林公式
对于麦克劳林可以得到函数的近似计算公式:
函数的近似计算
对于其误差有如下不等式成立:
麦克劳林公式的误差
<h1 class="pgc-h-arrow-right" data-track="30">五个重要常用麦克劳林公式</h1>
常用函数的泰勒展开式
<h1 class="pgc-h-arrow-right" data-track="33">几点说明</h1>
函数在同一点的泰勒公式是唯一的
带佩亚诺余项的泰勒公式主要描述的是x的在x0附件的函数性质
带拉格朗日余项的泰勒公式主要描述的是x在开区间(a,b)的性质
未完待续...