深度學習與統計力學(V) ：深度學習的泛化能力

谷歌和斯坦福最新合作綜述報告，發表在實體學的頂級期刊“凝聚态實體年鑒”（Annual Review of Condensed Matter Physics）。作者Yasaman Bahri, Jonathan Kadmon, Jeffrey Pennington, Sam S. Schoenholz, Jascha Sohl-Dickstein, and Surya Ganguli  

本公衆号将對本報告進行翻譯，分6次釋出。擷取英文報告請在本公衆号回複關鍵詞“深度學習統計力學”。

系列預告

• ​​深度學習與統計力學(I) ：深度學習中的基礎理論問題​​
• ​​深度學習與統計力學(II) ：深度學習的表達能力​​
• ​​深度學習與統計力學(III) ：神經網絡的誤差曲面​​
• ​​深度學習與統計力學(IV) ：深層網絡的信号傳播和初始化​​
• 深度學習與統計力學(V) ：深度學習的泛化能力
• 深度學習與統計力學(VI) ：通過機率模型進行“深度想象”

深度學習中的一個關鍵問題是了解何時以及為何深層網絡有着好的泛化能力？僅僅用一個包含 個樣本的有限資料集 ，針對 個參數 最小化公式(3)中的訓練誤差 ，網絡能夠在測試集上精确地進行預測，獲得公式(2)所示的較低的測試誤差 。深度學習處理的問題中， 可以大 幾個數量級，甚至

1 經典泛化理論：計算機科學 VS 實體學

在計算機科學中經典泛化理論[111]将任意學習過程表示為一個函數 。 将任意有限訓練集 映射到某個函數空間 中的一個特定函數 ，即 。資料本身通常是從一個真實函數 中（随機）生成的，當 和

當對所有真實函數 選取資料集 時以很高的機率成立。其中 是函數類 複雜度的某種度量。一個主要的度量是 Vapnik–Chervonenkis 次元[112]。對于很多神經網絡，Vapnik–Chervonenkis 次元随着參數數量 而增長。公式(11)中的 也可以替換為 Rademacher 複雜度 ，它度量了從 中選取的一個函數與 個随機噪音模式的相關性[113,114]。直覺上，如果 很大，且函數類 不是很複雜，則

另一個了解泛化能力的架構是算法穩定性的概念[115]，即如果對訓練資料 進行擾動時，由算法 得到的函數

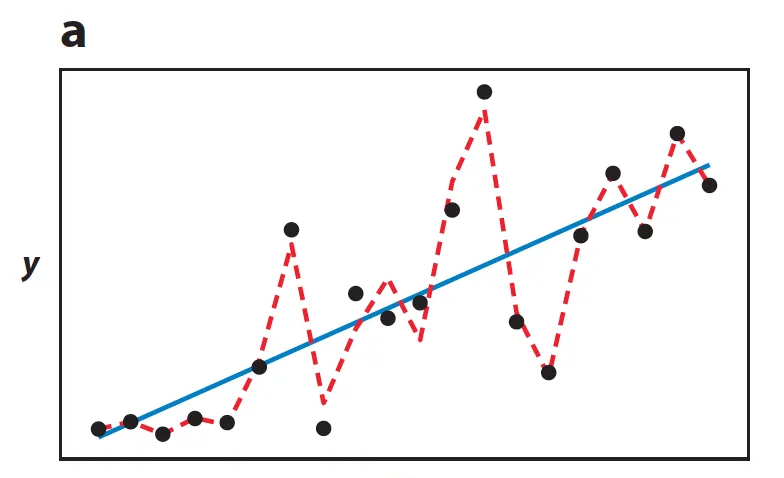
圖 5a 考慮一個從真實函數 ​ 加上噪聲生成的包含 ​ 個點的有限資料集 ​（圖中黑色點）。在一個簡單的線性函數空間 ​ 上最小化訓練誤差能夠得到一個對訓練資料擾動穩定的函數（藍色線），其在訓練資料上的泛化能力也較好。在一個更加複雜的分段線性函數空間上最小化則得到一個訓練誤差更優但是既不穩定泛化能力也差的函數（紅色虛線）。

然而，許多上述想法應用到從大小為 的訓練集中訓練的規模為 的大型神經網絡，當 遠大于

在實體領域大量有關神經網絡泛化方面的研究正在開展。然而實體領域側重的不再是推導測試誤差的上界，而是在熱力學極限下漸進精确地計算訓練誤差和測試誤差。熱力學極限是指 和 同時很大，但是測量密度 保持為 [126-128]（文獻11給出了更詳細的讨論）。在這種架構下包含 個點的訓練集 是從随機輸入和真實參數為 的教師神經網絡的輸出中采樣得到。訓練誤差 可以看作是一個學生神經網絡的熱自由度 上的能量函數，此時資料 的角色為淬火無序。然後将學生網絡參數 的統計力學系統的基态與教師網絡的權 進行比較來評估泛化能力。已經存在大量采用這種方法的工作[11]，然而對這種複雜的現代神經網絡進行計算，以及分析證明在 很小的現實結構的資料集

2 線性模型的經驗