連結：https://ac.nowcoder.com/acm/problem/20577
來源：牛客網
題目描述
小Z有一片森林，含有N個節點，每個節點上都有一個非負整數作為權值。初始的時候，森林中有M條邊。
小Z希望執行T個操作，操作有兩類：
Q x y k查詢點x到點y路徑上所有的權值中，第k小的權值是多少。此操作保證點x和點y連通，同時這兩個節點的路徑上至少有k個點。
L x y在點x和點y之間連接配接一條邊。保證完成此操作後，仍然是一片森林。
為了展現程式的線上性，我們把輸入資料進行了加密。設lastans為程式上一次輸出的結果，初始的時候lastans為0。
對于一個輸入的操作Q x y k,其真實操作為Q x^lastans y^lastans k^lastans。
對于一個輸入的操作L x y，其真實操作為L x^lastans ylastans。其中運算符表示異或，等價于pascal中的xor運算符。
請寫一個程式來幫助小Z完成這些操作。
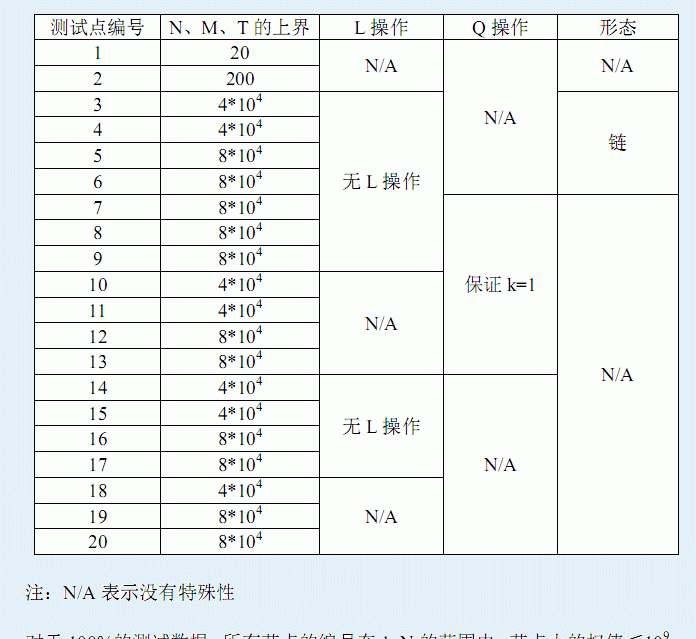
對于所有的資料，n,m,T<= 8∗10^4.
輸入描述:
第一行包含一個正整數testcase，表示目前測試資料的測試點編号。保證1<=testcase<=20。
第二行包含三個整數N，M，T，分别表示節點數、初始邊數、操作數。
第三行包含N個非負整數表示 N個節點上的權值。
接下來 M行，每行包含兩個整數x和 y，表示初始的時候，點x和點y 之間有一條無向邊。
接下來 T行，每行描述一個操作，格式為”Q x y k“或者”L x y “，其含義見題目描述部分。
輸出描述:
對于每一個第一類操作，輸出一個非負整數表示答案。
示例1
輸入
複制
1
8 4 8
1 1 2 2 3 3 4 4
4 7
1 8
2 4
2 1
Q 8 7 3 Q 3 5 1
Q 10 0 0
L 5 4
L 3 2 L 0 7
Q 9 2 5 Q 6 1 6
輸出
複制
2
2
1
4
2
備注:
很毒瘤的一道題目。
第一個輸入的不是組數，而是樣例的測試編号。。
對于求路徑上第k小，就是主席樹的闆子。
但是對于合并兩棵樹，就需要點技巧的。類似于并查集一樣的，就需要小的往大的上面合并。這樣的話，耗時是最小的。總之這道題目很煩，不知道哪兒寫錯了，在洛谷上面隻拿到了70分。。
代碼如下：
洛谷70分
#include<bits/stdc++.h>
#define ll long long
using namespace std;
const int maxx=1e5+100;
struct node{
int l;
int r;
int num;
}p[maxx*600];
struct edge{
int next,to;
}e[maxx<<1];
int head[maxx<<1],a[maxx],b[maxx],fa[maxx];
int size[maxx],deep[maxx],dp[maxx][25],vis[maxx],root[maxx];
int n,m,tot,ror,k,len;
/*-----------事前準備----------*/
inline void init()
{
memset(head,-1,sizeof(head));
memset(dp,0,sizeof(dp));
memset(deep,0,sizeof(deep));
memset(size,0,sizeof(size));
memset(vis,0,sizeof(vis));
tot=ror=0;
}
inline void add(int u,int v)
{
e[tot].to=v,e[tot].next=head[u],head[u]=tot++;
}
inline int read(){
int x=0;char ch=' ';int f=1;
while(ch!='-'&&(ch<'0'||ch>'9'))ch=getchar();
if(ch=='-')f=-1,ch=getchar();
while(ch>='0'&&ch<='9')x=x*10+ch-'0',ch=getchar();
return x*f;
}
/*----------主席樹-----------*/
inline int build(int l,int r)
{
int cur=++ror;
p[cur].num=0;
if(l==r) return cur;
int mid=l+r>>1;
p[cur].l=build(l,mid);
p[cur].r=build(mid+1,r);
return cur;
}
inline int update(int rot,int l,int r,int pos)
{
int cur=++ror;
p[cur]=p[rot];
p[cur].num++;
if(l==r) return cur;
int mid=l+r>>1;
if(pos<=mid) p[cur].l=update(p[rot].l,l,mid,pos);
else p[cur].r=update(p[rot].r,mid+1,r,pos);
return cur;
}
inline int query(int lrot,int rrot,int frot,int ffrot,int l,int r,int k)
{
if(l==r) return l;
int mid=l+r>>1;
int ret=p[p[lrot].l].num+p[p[rrot].l].num-p[p[frot].l].num-p[p[ffrot].l].num;
if(k<=ret) return query(p[lrot].l,p[rrot].l,p[frot].l,p[ffrot].l,l,mid,k);
else return query(p[lrot].r,p[rrot].r,p[frot].r,p[ffrot].r,mid+1,r,k-ret);
}
/*------------dfs------------*/
inline void dfs(int u,int f,int rt)
{
deep[u]=deep[f]+1;
dp[u][0]=f;
size[rt]++;//不斷記錄以rt為根節點的樹的節點個數有多少
for(int i=1;i<=20;i++)
{
if(dp[u][i-1]) dp[u][i]=dp[dp[u][i-1]][i-1];
else break;
}
vis[u]=1;
root[u]=update(root[f],1,len,lower_bound(b+1,b+1+len,a[u])-b);
for(int i=head[u];i!=-1;i=e[i].next)
{
int to=e[i].to;
if(to==f) continue;
dfs(to,u,rt);
}
}
/*----------并查集路徑壓縮----------*/
inline int getf(int u)//找根節點，很巧妙的一個地方
{
return u==fa[u]?fa[u]:(fa[u]=getf(fa[u]));
}
/*-----------lca-----------*/
inline int get_lca(int x,int y)
{
if(deep[x]<deep[y]) swap(x,y);
int tmp=deep[x]-deep[y];
for(int i=0;i<=20;i++)
{
if(tmp&(1<<i)) x=dp[x][i];
}
if(x==y) return x;
for(int i=20;i>=0;i--)
{
if(dp[x][i]!=dp[y][i])
{
x=dp[x][i];
y=dp[y][i];
}
}
return dp[x][0];
}
int main()
{
int t,x,y,d;char c;
t=read();
//while(t--)
//{
n=read(),m=read(),k=read();
init();
for(int i=1;i<=n;i++)
{
a[i]=read();
vis[i]=0;
fa[i]=i;
b[i]=a[i];
}
sort(b+1,b+1+n);
len=unique(b+1,b+1+n)-b-1;
for(int i=1;i<=m;i++)
{
x=read();y=read();
add(x,y),add(y,x);
}
root[0]=build(1,len);
for(int i=1;i<=n;i++) //先把所有的樹跑一邊，記錄深度，父節點以及節點個數
{
if(!vis[i])
{
dfs(i,0,i);
fa[i]=i;
}
}
int ans=0;
while(k--)
{
getchar();
scanf("%c",&c);
if(c=='Q')
{
x=read(),y=read(),d=read();
x^=ans,y^=ans,d^=ans;
int Lca=get_lca(x,y);
ans=b[query(root[x],root[y],root[Lca],root[dp[Lca][0]],1,len,d)];
printf("%d\n",ans);
}
else
{
x=read(),y=read();
x^=ans,y^=ans;
add(x,y);add(y,x);
int t1=getf(x);
int t2=getf(y);
if(size[t1]<size[t2]) dfs(x,y,t2);
else dfs(y,x,t1);//小的往大的上面合并
}
}
//}
}
滿分代碼：
#include<cstdio>
#include<cstring>
#include<iostream>
#include<cmath>
#include<algorithm>
#include<cstdlib>
#define ll long long
using namespace std;
inline int read(){
int x=0;char ch=' ';int f=1;
while(ch!='-'&&(ch<'0'||ch>'9'))ch=getchar();
if(ch=='-')f=-1,ch=getchar();
while(ch>='0'&&ch<='9')x=x*10+ch-'0',ch=getchar();
return x*f;
}
struct edge{
int to,next;
}e[320001];
int T,n,m,q,tot;
int a[80001];
int fa[80001];
int son[80001];
int head[80001];
inline void addedge(int x,int y){
e[++tot].to=y;e[tot].next=head[x];head[x]=tot;
}
struct Node{
int size,ls,rs;
}t[80001*600];
int cnt;
int root[80001];
void build(int &now,int l,int r){
now=++cnt;
t[now].size=0;
if(l==r)return;
int mid=(l+r)>>1;
build(t[now].ls,l,mid);
build(t[now].rs,mid+1,r);
}
void insert(int &now,int pre,int l,int r,int x){
now=++cnt;
t[now]=t[pre];
t[now].size++;
if(l==r)return;
int mid=(l+r)>>1;
if(x<=mid)insert(t[now].ls,t[pre].ls,l,mid,x);
else insert(t[now].rs,t[pre].rs,mid+1,r,x);
}
int b[80001];
int size;
int query(int x,int y,int pre1,int pre2,int l,int r,int k){
if(l==r)return b[l];
int lsize=t[t[x].ls].size+t[t[y].ls].size-t[t[pre1].ls].size-t[t[pre2].ls].size;
int mid=(l+r)>>1;
if(k<=lsize)return query(t[x].ls,t[y].ls,t[pre1].ls,t[pre2].ls,l,mid,k);
else return query(t[x].rs,t[y].rs,t[pre1].rs,t[pre2].rs,mid+1,r,k-lsize);
}
inline int Hash(int x){
return lower_bound(b+1,b+size+1,x)-b;
}
int find(int x){
return fa[x]==x?x:fa[x]=find(fa[x]);
}
int st[80001][17];
int dep[80001];
int vis[80001];
void dfs(int x,int father,int rt){
st[x][0]=father;
for(int k=1;k<=16;k++){
st[x][k]=st[st[x][k-1]][k-1];
}
son[rt]++;
dep[x]=dep[father]+1;
fa[x]=father;
vis[x]=1;
insert(root[x],root[father],1,size,Hash(a[x]));
for(int i=head[x];i;i=e[i].next){
int u=e[i].to;
if(u==father)continue;
dfs(u,x,rt);
}
}
inline int getlca(int x,int y){
if(x==y)return x;
if(dep[x]>dep[y])swap(x,y);
for(int k=16;k>=0;k--){
if(dep[st[y][k]]>=dep[x]){
y=st[y][k];
}
}
if(x==y)return x;
for(int k=16;k>=0;k--){
if(st[x][k]!=st[y][k]){
x=st[x][k];
y=st[y][k];
}
}
return st[x][0];
}
int main(){
T=read();
T=1;
while(T--){
memset(head,0,sizeof(head));
memset(dep,0,sizeof(dep));
memset(vis,0,sizeof(vis));
memset(st,0,sizeof(st));
memset(son,0,sizeof(son));
tot=0;
cnt=0;
n=read();m=read();q=read();
for(int i=1;i<=n;i++){
a[i]=read();
b[i]=a[i];
fa[i]=i;
}
sort(b+1,b+n+1);
size=unique(b+1,b+n+1)-b-1;
for(int i=1;i<=m;i++){
int x=read(),y=read();
addedge(x,y);addedge(y,x);
}
build(root[0],1,size);
for(int i=1;i<=n;i++){
if(!vis[i]){
dfs(i,0,i);
fa[i]=i;
}
}
int lastans=0;
for(int i=1;i<=q;i++){
char ch[3];
int x,y,k;
scanf("%s",ch);
x=read()^lastans;
y=read()^lastans;
if(ch[0]=='Q'){
k=read()^lastans;
int lca=getlca(x,y);
lastans=query(root[x],root[y],root[lca],root[st[lca][0]],1,size,k);
printf("%d\n",lastans);
}
else{
addedge(x,y);
addedge(y,x);
int u=find(x);
int v=find(y);
if(son[u]<son[v]){
swap(u,v);
swap(x,y);
}
dfs(y,x,u);
}
}
}
return 0;
}
乞求路過的大佬看看哪兒不對，跪謝。
十一假期開啟，codeforces之路起航
努力加油a啊，(o)/~
![LCA離線+線上+hdu2586(模闆)How far away ？[圖]](data:image/gif;base64,R0lGODlhAQABAIAAAP///wAAACwAAAAAAQABAAACAkQBADs=)