xDeepFM 網絡介紹與源碼淺析
前言 (與主題無關, 可以忽略)
哈哈哈, 十月第一篇部落格, 希望這個季度能更奮進一些~~~ 不想當鹹魚了… ????????????
廣而告之
可以在微信中搜尋 “珍妮的算法之路” 或者 “world4458” 關注我的微信公衆号;另外可以看看知乎專欄 PoorMemory-機器學習, 以後文章也會發在知乎專欄中;
xDeepFM
文章資訊
- 論文标題: xDeepFM: Combining Explicit and Implicit Feature Interactions for Recommender Systems
- 論文位址:https://arxiv.org/abs/1803.05170
- 代碼位址:https://github.com/Leavingseason/xDeepFM, 此外, DeepCTR 也進行了實作:https://github.com/shenweichen/DeepCTR/blob/master/deepctr/models/xdeepfm.py
- 發表時間: 2018
- 論文作者: Jianxun Lian, Xiaohuan Zhou, Fuzheng Zhang, Zhongxia Chen, Xing Xie, Guangzhong Sun
- 作者機關: University of Science and Technology of China
核心觀點
- xDeepFM (eXtreme Deep Factorization Machine) 的目的是為了處理特征交叉的問題, 可以視為是對 DCN 進行改進. 文章對 DCN 的特征交叉公式進行了觀察和推導, 發現 Cross 在做特征交叉其形式受限于一個特殊的形式, 其交叉特征表示為一個 scalar和輸入特征的乘積. 當然, 這裡的是有
- xDeepFM 的改進是: 首先特征交叉是在 vector-wise 的層級上做的, 并且和 DCN 的 Cross 層一樣, 本文介紹的 CIN (Compressed Interaction Network) 層對交叉特征進行顯式地學習,這樣就可以知曉特征的階數;
- CIN 進行特征交叉的具體過程是: 對于第層 CIN, 其使用第層的個特征和原始的輸入中的個特征進行特征交叉, 生成個交叉特征, 然後使用對這些特征進行權重求和 (每個交叉特征對應一個權重參數, 是以權重參數的個數為), 這樣就得到了一個輸出的交叉特征; 由于第層使用個權重矩陣, 那麼最後就可以得到
- xDeepFM 的輸入到輸出層的結果包含三部分, 分别對應着線性層, CIN 層以及 Deep 層的輸出結果,其中線性層包含着低階特征, CIN 層包含顯式學習的高階特征, 而 Deep 層包含隐式學習的高階特征.
核心觀點介紹
首先看 xDeepFM 的網絡結構, 如下圖所示:
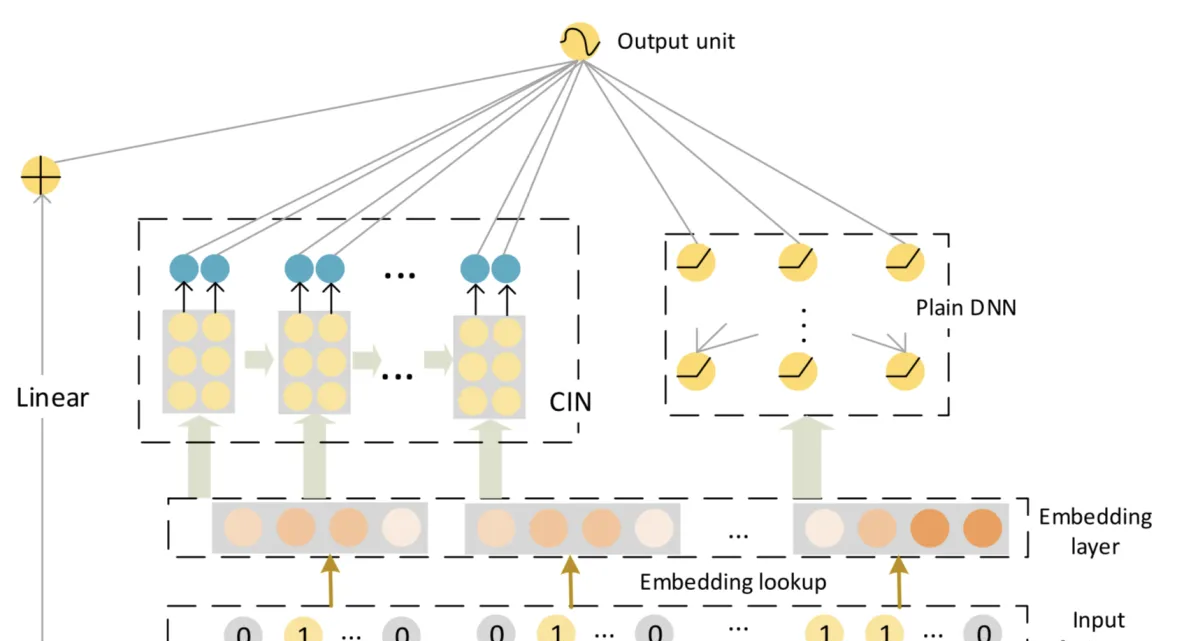
可以看到, 其結構類似于 Wide & Deep 與 DCN 結構, 不過其主要包含三個部分, 分别為線性層, CIN 層以及 Deep 層, 設 為 raw features, 為 DNN 的輸出結果,
可以認為 xDeepFM 是對 DCN 的改進, 其介紹了 CIN 層來替換 DCN 中的 Cross 層, 用于顯式學習交叉特征.
高階特征交叉 (High-order Interactions)
下面在介紹 CIN 層的原理之前, 先說明一下 Cross 層存在的問題, 這個是 xDeepFM 這篇 paper 讨論的一個重點. 為了友善讨論, 先引入一些必要的符号. 設原始的高維稀疏特征經 Embedding Layer 處理後, 映射為低維的稠密向量:
其中 表示 Field 的個數, 表示第 個 Field 所對應的 embedding. 是以對于一個樣本來說, 它對應的 embedding 大小為 .
在讨論 DCN 中的 Cross 層之前, 先介紹兩個概念:
-
隐式高階特征交叉(Implicit High-order Interactions): DNN 學習特征交叉的方式是隐式的, 因為DNN 最後表示的函數是任意的, 而且目前沒有理論論證了 DNN 能學習的特征交叉的最大階數.
(此處再插入對
bit-wise
vector-wise
bit
- 顯式高階特征交叉(Explicit High-order Interactions): 即學習到的交叉特征其階數是知曉的, 比如 FM 學習到的是二階特征交叉. DCN 中 Cross 層的目的也是希望顯式地對高階特征交叉進行模組化.
DCN 中 Cross 層通過下式對高階特征交叉進行模組化:
其中 分别為第 層的權重, bias 以及輸出. 作者認為 Cross 層學習出來的是一類特殊的高階特征交叉, 其表示為一個 scalar 和輸入特征 的乘積. 當然, 這裡的 是有
當
其中 為一個 scalar, 是以 可以表示為一個 scalar 和 的乘積. 使用數學歸納法, 假設這一點對 時仍然成立, 那麼當
其中 是一個 scalar. 是以 仍然是一個 scalar 和 的乘積. 是以可以證明, Cross 層的輸出确實滿足一種特殊的形式, 即 是一個 scalar 和
Cross 層可以高效的對高階交叉特征進行顯式地學習, 但問題是其結果受限于一個特殊的形式, 并且特征交叉是在 bit-wise level 而不是 vector-wise level 上. (另外注意, 雖然 可以表示為一個 scalar 和 的乘積, 但并不意味着 和 是線性關系, 因為系數 是跟
基于以上考慮, 本文提出 CIN 子產品, 一種新的對特征進行顯式交叉的方法, 并且特征交叉是在 vector-wise level 上進行的.
CIN (Compressed Interaction Network)
假設 Embedding Layer 的輸出為 , 其中 表示 field 的個數, 表示每個 field 所對應的 embedding 的大小, 第 行表示第 個 field 所對應的 embedding, 即 . CIN 的第 層輸出也是一個矩陣 , 其中 表示第 層的特征數量, 此外, 我們設定 . CIN 的計算過程可以用下圖表示:
對于 CIN 中的每一層來說, 其輸出
其中 , 表示第 個特征所對應的參數矩陣. 表示哈達瑪積 (Hadamard product), 比如對于向量 .
注意到 是通過 和
上圖中的 () 給出了 CIN 整體的結構, 假設 CIN 總共有 層, 在得到每層的輸出結果 () 後, 對結果中的每個 feature map 進行 sum pooling, 即:
其中 . 是以我們可以得到經過 pooling 後的 vector: , 其中 表示第
即
最後再讨論下 CIN 層的參數個數, 對于第 層來說, 其權重參數個數為 , 那麼總共有 個參數 (論文中考慮了輸出層的 個參數, 是以總共為
CIN 源碼淺析
原作者在 https://github.com/Leavingseason/xDeepFM/blob/master/exdeepfm/src/CIN.py 中實作了 CIN, 由于代碼有點多, 不太想看, 這裡分析 DeepCTR 對于 CIN 的實作, 了解個大概就行, 要用到的時候再說 ???? ???? ????
DeepCTR 在 https://github.com/shenweichen/DeepCTR/blob/master/deepctr/layers/interaction.py 中實作了
CIN
子產品.
詳細注釋寫在了代碼中, 其中不太直覺的地方有兩處, 我寫了很簡單的測試用例, 可以用于後續的參考:
-
dot_result_m = tf.matmul(split_tensor0, split_tensor, transpose_b=True)
import tensorflow as tf
B = 2
D = 3
m = 2
H = 2 ## 了解為 H_{k-1}
a = tf.reshape(tf.range(B * D * m, dtype=tf.float32),
(B, m, D))
b = tf.split(a, D * [1], 2)
c = tf.matmul(b, b, transpose_b=True)
with tf.Session() as sess:
print(sess.run(tf.shape(c))) ## shape 為 [D, B, m, H_{k-1}] -
curr_out = tf.nn.conv1d(dot_result, filters=self.filters[idx], stride=1, padding='VALID')
import tensorflow as tf
B = 2
D = 3
E = 4 ## 代表 m * H_{k-1}
F = 5 ## 代表 H_{k}
a = tf.reshape(tf.range(B * D * E, dtype=tf.float32),
(B, D, E))
b = tf.reshape(tf.range(1 * E * F, dtype=tf.float32),
(1, E, F))
curr_out = tf.nn.conv1d(
a, filters=b, stride=1, padding='VALID')
with tf.Session() as sess:
print(sess.run(tf.shape(curr_out))) ## 結果為 [B, D, H_{k}] class CIN(Layer):
"""Compressed Interaction Network used in xDeepFM.This implemention is
adapted from code that the author of the paper published on https://github.com/Leavingseason/xDeepFM.
Input shape
- 3D tensor with shape: ``(batch_size,field_size,embedding_size)``.
Output shape
- 2D tensor with shape: ``(batch_size, featuremap_num)`` ``featuremap_num = sum(self.layer_size[:-1]) // 2 + self.layer_size[-1]`` if ``split_half=True``,else ``sum(layer_size)`` .
Arguments
- **layer_size** : list of int.Feature maps in each layer.
- **activation** : activation function used on feature maps.
- **split_half** : bool.if set to False, half of the feature maps in each hidden will connect to output unit.
- **seed** : A Python integer to use as random seed.
References
- [Lian J, Zhou X, Zhang F, et al. xDeepFM: Combining Explicit and Implicit Feature Interactions for Recommender Systems[J]. arXiv preprint arXiv:1803.05170, 2018.] (https://arxiv.org/pdf/1803.05170.pdf)
"""
def __init__(self, layer_size=(128, 128), activation='relu', split_half=True, l2_reg=1e-5, seed=1024, **kwargs):
if len(layer_size) == 0:
raise ValueError(
"layer_size must be a list(tuple) of length greater than 1")
self.layer_size = layer_size
self.split_half = split_half
self.activation = activation
self.l2_reg = l2_reg
self.seed = seed
super(CIN, self).__init__(**kwargs)
def build(self, input_shape):
if len(input_shape) != 3:
raise ValueError(
"Unexpected inputs dimensions %d, expect to be 3 dimensions" % (len(input_shape)))
self.field_nums = [int(input_shape[1])]
self.filters = []
self.bias = []
for i, size in enumerate(self.layer_size):
## layer_size 對應着論文中的 H_{k}, 表示 CIN 每層中 feature map 的個數
## self.filters[i] 的 shape 為 [1, m * H_{k-1}, H_{k}]
self.filters.append(
self.add_weight(name='filter' + str(i),
shape=[1, self.field_nums[-1] * self.field_nums[0], size],
dtype=tf.float32, initializer=glorot_uniform(seed=self.seed + i),
regularizer=l2(self.l2_reg)))
## self.bias[i] 的 shape 為 [H_{k}]
self.bias.append(
self.add_weight(name='bias' + str(i),
shape=[size], dtype=tf.float32,
initializer=tf.keras.initializers.Zeros()))
if self.split_half:
if i != len(self.layer_size) - 1 and size % 2 > 0:
raise ValueError(
"layer_size must be even number except for the last layer when split_half=True")
self.field_nums.append(size // 2)
else:
self.field_nums.append(size)
self.activation_layers = [activation_layer(
self.activation) for _ in self.layer_size]
super(CIN, self).build(input_shape) # Be sure to call this somewhere!
def call(self, inputs, **kwargs):
## inputs 的 shape 為 [B, m, D], 其中 m 為 Field 的數量,
## D 為 embedding size, 我注釋的符号盡量和論文中的一樣
if K.ndim(inputs) != 3:
raise ValueError(
"Unexpected inputs dimensions %d, expect to be 3 dimensions" % (K.ndim(inputs)))
dim = int(inputs.get_shape()[-1]) # D
hidden_nn_layers = [inputs]
final_result = []
## split_tensor0 表示 list: [x1, x2, ..., xD], 其中 xi 的 shape 為 [B, m, 1]
split_tensor0 = tf.split(hidden_nn_layers[0], dim * [1], 2)
for idx, layer_size in enumerate(self.layer_size):
## split_tensor 表示 list: [t1, t2, ..., tH_{k-1}], 即有 H_{k-1} 個向量;
## 其中 ti 的 shape 為 [B, H_{k-1}, 1]
split_tensor = tf.split(hidden_nn_layers[-1], dim * [1], 2)
## dot_result_m 為一個 tensor, 其 shape 為 [D, B, m, H_{k-1}]
dot_result_m = tf.matmul(
split_tensor0, split_tensor, transpose_b=True)
## dot_result_o 的 shape 為 [D, B, m * H_{k-1}]
dot_result_o = tf.reshape(
dot_result_m, shape=[dim, -1, self.field_nums[0] * self.field_nums[idx]])
## dot_result 的 shape 為 [B, D, m * H_{k-1}]
dot_result = tf.transpose(dot_result_o, perm=[1, 0, 2])
## 牛掰啊, 還可以這樣寫, 精彩!
## self.filters[idx] 的 shape 為 [1, m * H_{k-1}, H_{k}]
## 是以 curr_out 的 shape 為 [B, D, H_{k}]
curr_out = tf.nn.conv1d(
dot_result, filters=self.filters[idx], stride=1, padding='VALID')
## self.bias[idx] 的 shape 為 [H_{k}]
## 是以 curr_out 的 shape 為 [B, D, H_{k}]
curr_out = tf.nn.bias_add(curr_out, self.bias[idx])
## curr_out 的 shape 為 [B, D, H_{k}]
curr_out = self.activation_layers[idx](curr_out)
## curr_out 的 shape 為 [B, H_{k}, D]
curr_out = tf.transpose(curr_out, perm=[0, 2, 1])
if self.split_half:
if idx != len(self.layer_size) - 1:
next_hidden, direct_connect = tf.split(
curr_out, 2 * [layer_size // 2], 1)
else:
direct_connect = curr_out
next_hidden = 0
else:
direct_connect = curr_out
next_hidden = curr_out
final_result.append(direct_connect)
hidden_nn_layers.append(next_hidden)
## 先假設不走 self.split_half 的邏輯, 此時 result 的
## shape 為 [B, sum(H_{k}), D] (k=1 -> T, T 為 CIN 的總層數)
result = tf.concat(final_result, axis=1)
## result 最終的 shape 為 [B, sum(H_{k})]
result = reduce_sum(result, -1, keep_dims=False)
return