最近在研究混沌時間序列,想了解基本知識,看的一本書叫做《混沌時間序列分析及其應用》(作者:呂金虎)(是中文書籍,不是翻譯的書籍)
書中第二章 混沌動力學 提到了幾個典型的混沌的例子
1.蟲口模型 Logistics
1.1 原理
蟲口模型---昆蟲變化的簡單數學模型。(昆蟲一次産卵的數量極大,子代出生後,其親代的數量可以忽略不計)認為昆蟲的種群是由單一的世代構成,在曆代之間沒有重疊。是以,昆蟲種群的增長(蟲口數)是分步進行的,例如,每個3年、5年或7年出現一次成蟲期的蟬就是這樣。
1.2 代碼
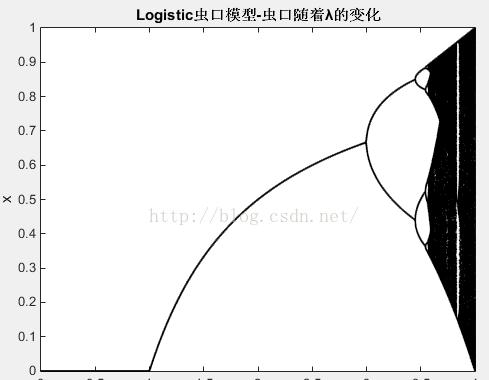
說明:首先進行一些疊代,使之大概達到一種有迹可循的狀态;然後就記錄結果。 橫軸可以看做是疊代次數,橫軸上的一點,對應的縱軸上很多個點的疊加。
%% -------------------蟲口模型-分岔圖----------- % 蟲口模型 x(n+1) = lambda * x(n) * (1 - x(n)) % 當 lambda 從 3 到 4 的過渡圖像 % 參見<<混沌動力學初步>>陳士華,陸君安編著 P46
clc clear close all
lambda = 0:5e-4:4;%原來是3:4 x = 0.4*ones(1,length(lambda));
N1 = 800; % 前面的疊代點數(原來是400) N2 = 200; % 後面的疊代點數(原來是100)
f = zeros(N1+N2,length(lambda)); for i = 1:N1+N2 x = lambda .* x .* (1 - x); f(i,:) = x; end f = f(N1+1:end,:);
plot(lambda,f,'k.','MarkerSize',1) xlabel('\lambda') ylabel('x'); title('Logistic蟲口模型-蟲口随着λ的變化')
1.3 結果
2.洛倫茲方程-天氣對流模型
2.1 原理
1963年,美國著名氣象學家洛倫茲在研究天氣預報問題時,發現确定性方程中出現混沌現象。
振蕩曲線與完全随機的噪聲不一樣,它似乎有一定的規律:無論時間多長,它都不會完全重複以前某時刻的振蕩,即此時振蕩具有非周期性和随機性。這些軌迹被限制在相平面(空間)的有限區域内,這樣的有限區域稱為動力系統的吸引子(attractor)。對于周期運動,吸引子是一條簡單的閉曲線。但形如洛倫茲系統這樣的具有随機性的費周期運動,其吸引子遠非什麼複雜的閉曲線,其軌線往往是反複折疊和互相交叉而形成的密集的帶。這種具有複雜結構的吸引子稱為奇怪吸引子(strange attractor)。具有奇怪吸引子的運動就是混沌的。
2.2 代碼
2.2.1 主函數
%本程式的作用:求解&繪圖
[t,y]=ode45('Lorenz',[0 30],[12,2,9]); (可以寫作: [t,y]=ode45(@Lorenz,[0 30],[12,2,9]) )
figure(1) plot(t,y(:,1));
title('x關于t的變化圖');
xlabel('t');
ylabel('x(t)');
figure(2)
plot(t,y(:,2));
title('y關于t的變化圖');
xlabel('t');
ylabel('y(t)');
figure(3)
plot(t,y(:,3));
title('z關于t的變化圖');
xlabel('t');
ylabel('z(t)');
figure(4)
plot3(y(:,1),y(:,2),y(:,3))
title({'x,y,z的空間關系圖','Lorenz方程在三維相空間中的軌迹圖形'}');
xlabel('x');ylabel('y'),zlabel('z');
view([20,32]);
%% ----驗證“蝴蝶效應”----------
%解釋:洛倫茲方程的解對初始值十分敏感,現在對y的初始值稍加修改,将2改為2.01和1.99,
% 然後求解z的數值解。
%結果說明:随着時間的推移,三條曲線的吻合程度越來越差,差距越來越大,變化也越來越不明顯,成為混沌狀态、。
% 前面一部分(t<5),三條曲線幾乎完全重合。
% clf %清楚目前figure内的圖形
figure(5)
hold on
[t,u]=ode45('Lorenz',[0 15],[12,2,9]);
plot(t,u(:,3),'Color','r');
[t,v]=ode45('Lorenz',[0 15],[12,2.01,9]);
plot(t,v(:,3),'Color','b');
[t,w]=ode45('Lorenz',[0 15],[12,1.99,9]);
plot(t,w(:,3),'Color','k');
hold off
legend('y(t=0)=2','y(t=0)=2.01','y(t=0)=1.99');
xlabel('t');
ylabel('z(t)');
title('蝴蝶效應-y的不同的初始值下,z的取值變化');
2.2.2 函數 Lorenz.m
% (1)洛倫茲方程是一組常微分方程,Runge-Kutta方法是求解常微分方程的經典方法,
% Matlab提供了多個采用該方法的函數指令:ode23 ,ode45 等。
% (2)下面采用ode45指令求解Lorenz在研究大氣對流模型時得到的洛倫茲方程:
% dx/dt=A*(-x+y)
% dy/dt=B*x-y-x*z
% dz/dt=x*y-C*z
% 經常引用的參數是: A=10,B=2,C=8/3 相空間維數為3
% (3)為了用Matlab求解,将x,y,z表示為y(1),y(2),y(3),即為列向量中的三個分量
function dy=Lorenz(t,y)
A=10;
B=28;
C=8/3;
dy=zeros(3,1);
dy(1)=A*(-y(1)+y(2));
dy(2)=B*y(1)-y(2)-y(1)*y(3);
dy(3)=y(1)*y(2)-C*y(3);
end
3.Chen's吸引子
3.1 微分方程求解
3.1.1定義函數Chens.m
function dy=Chens(t,y)
dy=zeros(3,1);%一個三行的矢量
A=35;
B=3;
C=28;
dy(1)=A*(y(2)-y(1));
dy(2)=(C-A)*y(1)-y(1)*y(3)+C*y(2);
dy(3)=y(1)*y(2)-B*y(3);
end
3.1.2求解方程
%二階、三階Runge-Kutta法積分,采用函數:ode23
%四階、五階Runge-Kutta法積分,采用函數:ode45
[T,Y]= ode45(@Chens,[0 200],[0 1 0]);
plot3(Y(:,1),Y(:,2),Y(:,3));
xlabel('x axis');ylabel('y axis');zlabel('z axis');
view(0,90);%在xoy面的投影
view(90,0);%在yoz面的投影
view(0,0);%在xoz面的投影
3.2 線性方程組求解
%% ---------求解平衡點---------------
syms x y z
[solx,soly,solz]= solve(35*(y-x) = =0,-7*x-x*z+28*y==0,x*y-3*z==0,x,y,z)
solutions=[solx,soly,solz] 求得的解如下: solutions =
[ 0, 0, 0]
[ -3*7^(1/2), -3*7^(1/2), 21]
[ 3*7^(1/2), 3*7^(1/2), 21]