leetcode 88 Merge Sorted Array 歸并排序

歸并排序：先将數組一分為二，将左邊部分排序（同樣将其一分為二），再将右邊部分排序，最後逐層歸并。（分治政策）（穩定排序）。

算法穩定性 -- 假設在數列中存在a[i]=a[j]，若在排序之前，a[i]在a[j]前面；并且排序之後，a[i]仍然在a[j]前面。則這個排序算法是穩定的！

先排序的時間複雜度為log(n)；

後歸并的時間複雜度為n；

總的時間複雜度nlog(n)。

1)自頂向下歸并排序的代碼：需要一個和待排序數組相同的空間，故将arr[]拷貝一份給aux[]

//将arr[l...mid]和 arr[mid+1...r]兩部分進行歸并
template<typename T>
void merge(T arr[], int l, int mid,  int r){
    //需要一個臨時的和arr同樣大小的空間
    T aux[r-l+1];
    for(int i=l;i<=r;i++)
        //将arr複制給aus,aus下标從0開始，而arr下标從l開始
        aux[i-l] = arr[i];
//初始化，i指向左半部分的起始索引位置l；j指向右半部分起始索引位置mid+1    
    int i = l, j = mid+1;
    for(int k=l;k<=r;k++){
        //逐漸比較左部分的第i個元素和右部分的第j個元素的大小
        //首先判斷下标i和j的合法性
        if(i>mid){
            //左邊已經周遊完，但右邊還有
            arr[k] = aux[j-l];
            j++
        }
        else if(j>r){
            //右邊已經周遊完，将左邊的元素給arr
            arr[k] = aux[i-l];
            i++;
        }
        else if(aux[i-l]<aux[j-l]){
            arr[k] = aux[i-l];
            i++;
        }
        else{
            arr[k] = aux[j-l];
            j++;
        }    
    }      
}

    
//遞歸使用歸并排序，對arr[l...r]的範圍進行排序
template<typename T>
void mergeSort(T arr[], int l, int r){
    if(l>=r)
        return;
    int mid = (l+r)/2;
    mergeSort(arr, l, mid);
    mergeSort(arr, mid+1,r);
    //優化：隻有當 mid>mid+1 時才需要對左右兩邊進行排序
    //因為左邊或右邊本身是有序的，如果 mid<=mid+1 則不需要對其歸并排序了
    if(arr[mid] > arr[mid+1])
        merge(arr,l,mid,r);
}      

 當數組中的元素足夠少時，可以将遞歸出口改為插入排序，雖然插入排序的時間複雜度是O(n),但是可以提高效率。

 2)自底向上歸并排序：

template<typename T>      //泛型
void mergeSortBU(T arr[], int n){
    //自底向上歸并
    //對merge的元素個數進行周遊：1，2，4，8以此類推
    for(int sz=1 ; sz<=n ; sz+=sz ){
        for(int i=0; i+sz<n; i+=sz+sz)
            //對arr[i...i+sz-1]和arr[i+sz...i+2*sz-1]進行歸并
            merge(arr, i, i+sz-1, min(i+sz+sz-1, n-1));
    }    
}      

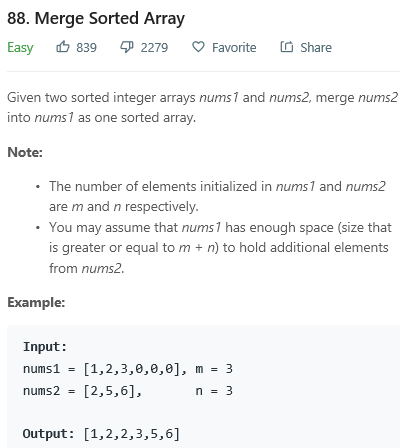
注意：nums1和nums2 是有序的，m代表nums1元素的個數。

這裡的解題思想是歸并排序的merge()函數的思想，先開辟一個與nums1相同大小和值的空間aux，再将其與nums2逐一對比，用小的來替換nums1的值。

class Solution {
public:
    void merge(vector<int>& nums1, int m, vector<int>& nums2, int n) {
        
        if (m <= 0 && n <= 0) return;
        //int aux[m];
        vector<int> aux(m);
        for(int i=0;i<m;i++){
            //将nums1的值拷貝給aux
            aux[i] = nums1[i];
        }
        
        int i=0,j=0;
        for(int k=0;k<nums1.size();k++){
            if(i>m-1){
                //aux數組超界
                nums1[k] = nums2[j];
                j++;
            }
            else if(j>n-1){
                nums1[k] = aux[i];
                i++;
            }    
            else if(nums2[j]<aux[i]){
                nums1[k] = nums2[j];
                j++;
            }
            else{
                nums1[k] = aux[i];
                i++;
            }
                
        }
    }
};      

解法二：從兩個數組的末尾開始比較大小，從下标為m+n-1開始存放，将大的存放在nums1的末尾。如果最後剩下的是nums1，則不需要移動；若是nums2中的元素則需要放在nums1的相應位置。

class Solution {
public:
    void merge(vector<int>& nums1, int m, vector<int>& nums2, int n) {
        
        if (m <= 0 && n <= 0) return;
        
        int count = m+n-1;
        --m, --n;   //m和n是長度，是以要減1變成下标
        while(m>=0 && n>=0){
            if(nums1[m] >nums2[n])
                nums1[count--] = nums1[m--];
            else
                nums1[count--] = nums2[n--];
        }    
        while(n>=0){
           //當m已經全部周遊完，n還剩下
            nums1[count--] = nums2[n--];
        }
    }
};      

轉載于:https://www.cnblogs.com/Bella2017/p/10126088.html