學習筆記,僅供參考,有錯必究
文章目錄
- 時間序列習題
- 機關根檢驗舉例
- 四種典型的非平穩随機過程
- DF 統計量和 t 統計量的分布特征
- 情形1
- 情形2
- 情形3
- DF 統計量的有限樣本分布特征總結
- 機關根檢驗
- AR(1)過程的機關根檢驗
- AR(p)過程的機關根檢驗
- 例子1: 421天的深證成指序列
- 例 2 :中國就業總人數序列
- 例 3 :人民币元兌美元匯率序列的機關根檢驗
時間序列習題
機關根檢驗舉例
四種典型的非平穩随機過程
- 随機遊走過程
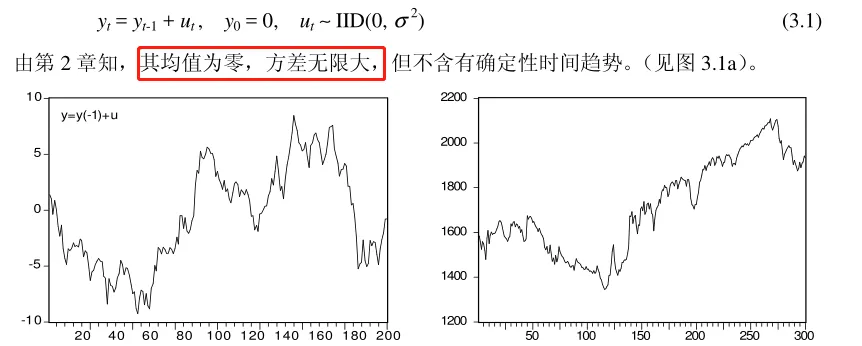
- 随機趨勢過程
對作一次差分後,序列就平穩了:
是以也稱為差分平穩過程(difference- stationary process)。 是序列的均值,原序列的增長速度。
- 趨勢平穩過程
- 趨勢非平穩過程
由上面 4 種随機過程走勢可以看出,對于對數的宏觀經濟變量,随機趨勢過程和退勢平穩過程是兩種最常見的表現形式。
下面分析随機趨勢過程與平穩的 AR(1)過程的差別。對于如下過程:
DF 統計量和 t 統計量的分布特征
在介紹檢驗方法之前,先讨論回歸系數統計量的分布。
情形1
是檢驗機關根的一個常用統計量。有三個結論如下:
- DF統計量
檢驗機關根的另一個統計量是統計量, 統計量在這裡稱 DF 統計量。當時:
情形2
情形3
DF 統計量的有限樣本分布特征總結
機關根檢驗
AR(1)過程的機關根檢驗
對于時間序列可用如下自回歸模型檢驗機關根:
以附表 6 中a部分的相應百分位數作為臨界值,若用樣本計算的:
DF > 臨界值,則接受 H 0 ,非平穩;
DF < 臨界值,則拒絕 H 0 ,是平穩的
- 注意
上述 DF 檢驗還可用另一種形式表達。(3.24) 式兩側同減,得:
這種變化并不影響 DF 統計量的值,是以檢驗規則仍然是:
若 DF > 臨界值,則 y t 是非平穩的;
若 DF < 臨界值,則 y t 是平穩的。
這種檢驗方法是 DF 檢驗的常用方法。
舉例說明以上兩種機關根檢驗方法的 DF 值相同。用同一組資料 y t 得到的兩個回歸結果
如下(括号内給出的是标準差):
注意:
AR§過程的機關根檢驗
以上方法隻适用于 AR(1) 過程的機關根檢驗。當時間序列為 AR§ 形式,或者由以上形式檢驗得到的殘差序列存在自相關時,應采用如下形式檢驗機關根:
注意:
例子1: 421天的深證成指序列
421 天的深證成指序列見圖 3.20。從序列走勢看決不會是随機趨勢非平穩序列,也不會是随機趨勢序列。
- 檢驗方法(1)
不妨先按随機趨勢序列設定檢驗式。帶有截距項的 DF 檢驗式的估計結果如下:
- 檢驗方法(2)
也可以用 F 統計量檢驗判斷漂移項的存在。對(3.35)式中兩個參數做都等于零的 F 檢
驗。
例 2 :中國就業總人數序列
1978-2004 年中國就業人員數( labor ,億人)序列如下圖:
從曲線變化情形看,這是一個帶有均值和斜率突變的非平穩序列。當加入虛拟變量 D1對這種變化進行描述時,就可以清楚地看到這一點。輸出結果如下:
輸出結果還可按兩個時期寫為:
用退勢的方法檢驗機關根。對( 3.46 )式作如下變換:
如果不考慮序列中的結構突變因素,直接用 ADF 檢驗式檢驗機關根,檢驗結果如下:
這個例子非常清楚地說明,中國就業人員數序列是一個退勢平穩序列。當序列存在結構突變,而又沒考慮到這種突變時,就會把一個退勢平穩序列錯判為含有機關根的序列。并再一次說明,當序列存在結構突變, ADF 檢驗式中如果不考慮這種結構突變,就會導緻 ADF檢驗的功效大大降低
例 3 :人民币元兌美元匯率序列的機關根檢驗
截取其中 1991:1∼1996:12 一段檢驗機關根。以 1993 年 12 月為突變點,設:
輸出結果如下:
D1 的系數有顯著性,說明序列确實存在結構變化。 t 和 (t-36)D1 項的系數都有顯著性,且前者為正,後者為負;說明并軌之前,人民币元兌美元的長期趨勢一直在貶值;而并軌之後,人民币元兌美元的長期趨勢一直在升值。
輸出結果還可按兩個時期寫為: