#yyds幹貨盤點# 面試必刷TOP101：二叉搜尋樹的最近公共祖先

1.簡述：

描述

給定一個二叉搜尋樹, 找到該樹中兩個指定節點的最近公共祖先。

1.對于該題的最近的公共祖先定義:對于有根樹T的兩個節點p、q，最近公共祖先LCA(T,p,q)表示一個節點x，滿足x是p和q的祖先且x的深度盡可能大。在這裡，一個節點也可以是它自己的祖先.

2.二叉搜尋樹是若它的左子樹不空，則左子樹上所有節點的值均小于它的根節點的值； 若它的右子樹不空，則右子樹上所有節點的值均大于它的根節點的值

3.所有節點的值都是唯一的。

4.p、q 為不同節點且均存在于給定的二叉搜尋樹中。​

資料範圍:

3<=節點總數<=10000

0<=節點值<=10000

如果給定以下搜尋二叉樹: {7,1,12,0,4,11,14,#,#,3,5}，如下圖:

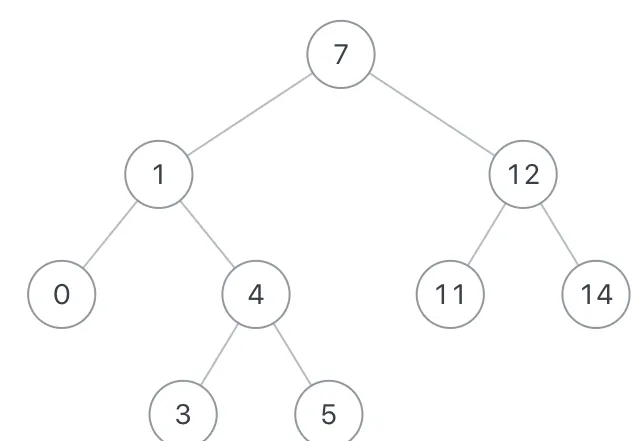
示例1

輸入：

{7,1,12,0,4,11,14,#,#,3,5},1,12      

傳回值：

7      

說明：

節點1 和 節點12的最近公共祖先是7      

示例2

輸入：

{7,1,12,0,4,11,14,#,#,3,5},12,11      

傳回值：

12      

因為一個節點也可以是它自己的祖先.是以輸出12      

import java.util.*;
public class Solution {
    //求得根節點到目标節點的路徑
    public ArrayList<Integer> getPath(TreeNode root, int target) {
        ArrayList<Integer> path = new ArrayList<Integer>();
        TreeNode node = root;
        //節點值都不同，可以直接用值比較
        while(node.val != target){ 
            path.add(node.val);
            //小的在左子樹
            if(target < node.val) 
                node = node.left;
            //大的在右子樹
            else 
                node = node.right;
        }
        path.add(node.val);
        return path;
    }
    public int lowestCommonAncestor (TreeNode root, int p, int q) {
        //求根節點到兩個節點的路徑
        ArrayList<Integer> path_p = getPath(root, p); 
        ArrayList<Integer> path_q = getPath(root, q);
        int res = 0;
        //比較兩個路徑，找到第一個不同的點
        for(int i = 0; i < path_p.size() && i < path_q.size(); i++){ 
            int x = path_p.get(i);
            int y = path_q.get(i);
            //最後一個相同的節點就是最近公共祖先
            if(x == y) 
                res = path_p.get(i);
            else
                break;
        }
        return res;
    }
}