1. 斐波那契數列
509. 斐波那契數
斐波那契數 (通常用 F(n) 表示)形成的序列稱為 斐波那契數列 。該數列由 0 和 1 開始,後面的每一項數字都是前面兩項數字的和。也就是:
F(0) = 0,F(1) = 1
F(n) = F(n - 1) + F(n - 2),其中 n > 1
給定 n ,請計算 F(n) 。
示例 1:
輸入:n = 2
輸出:1
解釋:F(2) = F(1) + F(0) = 1 + 0 = 1
示例 2:
輸入:n = 3
輸出:2
解釋:F(3) = F(2) + F(1) = 1 + 1 = 2
示例 3:
輸入:n = 4
輸出:3
解釋:F(4) = F(3) + F(2) = 2 + 1 = 3
提示:
0 <= n <= 30
題解:
class Solution:
def fib(self, n: int) -> int:
if n == 0:
return 0
if n == 1:
return 1
dp = [0] * (n + 1) # 定義 dp 數組
dp[0] = 0 # 初始化
dp[1] = 1
for i in range(2, n+1):
dp[i] = dp[i - 1] + dp[i - 2] # 遞推公式
return dp[n]
2. 爬樓梯
70. 爬樓梯
假設你正在爬樓梯。需要 n 階你才能到達樓頂。
每次你可以爬 1 或 2 個台階。你有多少種不同的方法可以爬到樓頂呢?
示例 1:
輸入:n = 2
輸出:2
解釋:有兩種方法可以爬到樓頂。
1. 1 階 + 1 階
2. 2 階
示例 2:
輸入:n = 3
輸出:3
解釋:有三種方法可以爬到樓頂。
1. 1 階 + 1 階 + 1 階
2. 1 階 + 2 階
3. 2 階 + 1 階
提示:
1 <= n <= 45
爬樓梯實質上也可以看作一個斐波拉契數列:
class Solution:
def climbStairs(self, n: int) -> int:
dp = [0] * (n+1)
dp[0] = 1
dp[1] = 1
for i in range(2, n+1):
dp[i] = dp[i-1] + dp[i-2]
return dp[n]
類似題目 劍指 Offer 10- II. 青蛙跳台階問題:
class Solution:
def numWays(self, n: int) -> int:
if n == 0 or n == 1:
return 1
dp = [0] * (n + 1)
dp[0] = 1 # 0 個台階有 1 種 方法
dp[1] = 1 # 1 個台階有 1 種方法
for i in range(2, n + 1):
dp[i] = dp[i - 1] + dp[i - 2]
return dp[n] % 1000000007
3. 不同路徑
62. 不同路徑
一個機器人位于一個 m x n 網格的左上角 (起始點在下圖中标記為 “Start” )。
機器人每次隻能向下或者向右移動一步。機器人試圖達到網格的右下角(在下圖中标記為 “Finish” )。
問總共有多少條不同的路徑?
示例 1:
輸入:m = 3, n = 7
輸出:28
示例 2:
輸入:m = 3, n = 2
輸出:3
解釋:
從左上角開始,總共有 3 條路徑可以到達右下角。
1. 向右 -> 向下 -> 向下
2. 向下 -> 向下 -> 向右
3. 向下 -> 向右 -> 向下
示例 3:
輸入:m = 7, n = 3
輸出:28
示例 4:
輸入:m = 3, n = 3
輸出:6
提示:
1 <= m, n <= 100
題目資料保證答案小于等于 2 * 109
題解一:
class Solution:
def uniquePaths(self, m: int, n: int) -> int:
dp = [[0 for i in range(n)] for j in range(m)]
def diff_path(row, col):
# 第一列的任意單元格,隻有來自它上一個單元格過來的方法
for i in range(n):
dp[0][i] = 1
# 第一行的任意單元格,隻有來自它前一個單元格過來的一種方法
for j in range(m):
dp[j][0] = 1
# 随意一個單元格有來自上或者左的兩種路徑,第一行、第一列已填充,不用繼續填充
for i in range(1, row):
for j in range(1, col):
dp[i][j] = dp[i - 1][j] + dp[i][j - 1]
# 傳回最後一個單元格的位置
return dp[row - 1][col - 1]
return diff_path(m, n)
題解二:(更容易了解)
class Solution:
def uniquePaths(self, m: int, n: int) -> int:
dp = [[0] * n for i in range(m)]
for row in range(m):
for col in range(n):
# 第一個格子隻有一種方法
if row == 0 and col == 0:
dp[row][col] = 1
elif col == 0:
# 第一行的任意單元格,隻有來自它前一個單元格過來的一種方法
dp[row][col] = dp[row-1][col]
elif row == 0:
# 第一列的任意單元格,隻有來自它上一個單元格過來的方法
dp[row][col] = dp[row][col - 1]
else:
# 其他情況(中間):任意一個單元格有來自其左或上兩個方向的機器人
dp[row][col] = dp[row - 1][col] + dp[row][col - 1]
return dp[m - 1][n - 1]
4. 不同路徑 II
63. 不同路徑 II
示例 1:
輸入:obstacleGrid = [[0,0,0],[0,1,0],[0,0,0]]
輸出:2
解釋:3x3 網格的正中間有一個障礙物。
從左上角到右下角一共有 2 條不同的路徑:
1. 向右 -> 向右 -> 向下 -> 向下
2. 向下 -> 向下 -> 向右 -> 向右
示例 2:
輸入:obstacleGrid = [[0,1],[0,0]]
輸出:1
提示:
m == obstacleGrid.length
n == obstacleGrid[i].length
1 <= m, n <= 100
obstacleGrid[i][j] 為 0 或 1
題解:
class Solution:
def uniquePathsWithObstacles(self, obstacleGrid: List[List[int]]) -> int:
row = len(obstacleGrid)
col = len(obstacleGrid[0])
# 隻有一個單元格,即一行一列時
if row == 1 and col == 1:
if obstacleGrid[0][0] == 1:
return 0
else:
return 1
dp = [[0] * col for i in range(row)]
for i in range(row):
for j in range(col):
# 遇到阻礙,就跳過目前循環
if obstacleGrid[i][j] == 1:
continue
if i == 0 and j == 0:
dp[i][j] = 1
elif i == 0:
dp[i][j] = dp[i][j - 1]
elif j == 0:
dp[i][j] = dp[i - 1][j]
else:
dp[i][j] = dp[i][j - 1] + dp[i - 1][j]
return dp[row - 1][col - 1]
5. 最小路徑和
64. 最小路徑和
給定一個包含非負整數的 m x n 網格 grid ,請找出一條從左上角到右下角的路徑,使得路徑上的數字總和為最小。
說明:每次隻能向下或者向右移動一步。
示例 1:
輸入:grid = [[1,3,1],[1,5,1],[4,2,1]]
輸出:7
解釋:因為路徑 1→3→1→1→1 的總和最小。
示例 2:
輸入:grid = [[1,2,3],[4,5,6]]
輸出:12
提示:
m == grid.length
n == grid[i].length
1 <= m, n <= 200
0 <= grid[i][j] <= 100
題解:
class Solution:
def minPathSum(self, grid: List[List[int]]) -> int:
m, n = len(grid), len(grid[0])
# 隻有一個單元格時
if m == 1 and n == 1:
return grid[0][0]
dp = [[0] * n for i in range(m)]
for i in range(m):
for j in range(n):
if i == 0:
# 第一行,和 = 目前單元格數字 + 前一個單元格數字
dp[i][j] = dp[i][j - 1] + grid[i][j]
elif j == 0:
# 第一列,和 = 目前單元格數字 + 上一個單元格數字
dp[i][j] = dp[i - 1][j] + grid[i][j]
else:
# 中間單元格,和 = 目前單元格數字 + 上一個和前一個單元格中最小的數字
dp[i][j] = min(dp[i][j - 1], dp[i - 1][j]) + grid[i][j]
return dp[m-1][n-1]
注意:代表的是狀态轉移,它包括前面走過的路徑之和,而dp[i][j - 1]、dp[i - 1][j]
代表的僅僅隻是目前單元格一個數字,是以是:grid[i][j]
,而不是dp[i][j] = dp[i][j - 1] + grid[i][j]
dp[i][j] = grid[i][j - 1] + grid[i][j]
6. 最長遞增子序列
300. 最長遞增子序列
給你一個整數數組 nums ,找到其中最長嚴格遞增子序列的長度。
子序列 是由數組派生而來的序列,删除(或不删除)數組中的元素而不改變其餘元素的順序。例如,[3,6,2,7] 是數組 [0,3,1,6,2,2,7] 的子序列。
示例 1:
輸入:nums = [10,9,2,5,3,7,101,18]
輸出:4
解釋:最長遞增子序列是 [2,3,7,101],是以長度為 4 。
示例 2:
輸入:nums = [0,1,0,3,2,3]
輸出:4
示例 3:
輸入:nums = [7,7,7,7,7,7,7]
輸出:1
提示:
1 <= nums.length <= 2500
-104 <= nums[i] <= 104
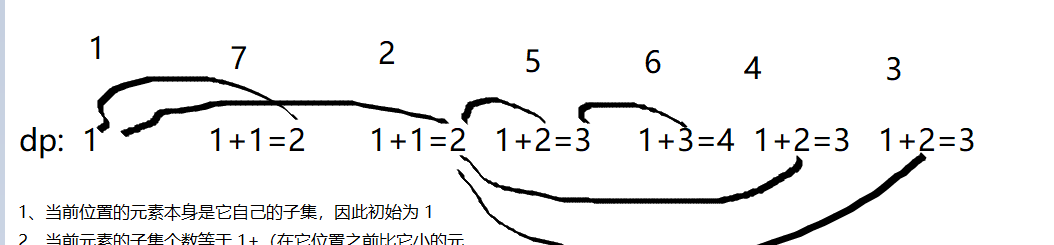
題解:
dp[i]
表示目前元素的遞增子集個數
- 元素 1: 因為沒有比它小的元素,是以遞增子集數為 1
- 元素 7:遞增子集有:
1、 17
1 + dp[0]
- 元素 2:遞增子集有:因為
7
2
1、 12
1 + dp[0]
- 元素 5:遞增子集有:
1 、 15、 125
1 + dp[2]
- 如此類推就能推出
dp[i]
class Solution:
def lengthOfLIS(self, nums: List[int]) -> int:
n = len(nums)
if n == 1:
return 1
dp = [1] * n
res = 1
for i in range(n):
for j in range(i):
# 目前元素與它之前所有的元素進行比較,若之前元素比目前元素大,則跳過不考慮,隻需要考慮比它小的即可
if nums[i] > nums[j]:
dp[i] = max(dp[j] + 1, dp[i])
res = max(res, dp[i])
return res
參考:【算法太難了】【23】最長遞增子序列-動态規劃
7. 最長公共子序列
1143. 最長公共子序列
給定兩個字元串 text1 和 text2,傳回這兩個字元串的最長 公共子序列 的長度。如果不存在 公共子序列 ,傳回 0 。
一個字元串的 子序列 是指這樣一個新的字元串:它是由原字元串在不改變字元的相對順序的情況下删除某些字元(也可以不删除任何字元)後組成的新字元串。
例如,"ace" 是 "abcde" 的子序列,但 "aec" 不是 "abcde" 的子序列。
兩個字元串的 公共子序列 是這兩個字元串所共同擁有的子序列。
示例 1:
輸入:text1 = "abcde", text2 = "ace"
輸出:3
解釋:最長公共子序列是 "ace" ,它的長度為 3 。
示例 2:
輸入:text1 = "abc", text2 = "abc"
輸出:3
解釋:最長公共子序列是 "abc" ,它的長度為 3 。
示例 3:
輸入:text1 = "abc", text2 = "def"
輸出:0
解釋:兩個字元串沒有公共子序列,傳回 0 。
題解:
對于兩個字元串求子序列的問題,都是用兩個指針
i
和
j
分别在兩個字元串上移動,大機率是動态規劃思路
class Solution:
def longestCommonSubsequence(self, text1: str, text2: str) -> int:
# dp 函數的定義:dp(s1, i, s2, j) 計算 s1[i..]和s2[j..]的最長公共子序列長度
dp = [[-1 for _ in text2] for _ in text1]
def ways(s1, i, s2, j):
# bad case,此時 s1 或 s2 相當于空串了
if len(s1) == i or len(s2) == j:
return 0
# 備忘錄,避免重複計算
if dp[i][j] != -1:
return dp[i][j]
# 比較兩個字元串是否相等,若相等一定這個字元串一定在 lcs 中
if s1[i] == s2[j]:
dp[i][j] = 1 + ways(s1, i+1, s2, j+1)
else:
# 不相等,則 s1[i] 、s2[j] 至少有一個不在 lcs 中
dp[i][j] = max(
ways(s1, i+1, s2, j), # s1[i] 不在 lcs 中
ways(s1, i, s2, j+1), # s2[j] 不在 lcs 中
ways(s1, i+1, s2, j+1) # 都不在 lcs 中(這一步可省略,因為前面兩步已經包含了)
)
return dp[i][j]
return ways(text1, 0, text2, 0)
8. 最長回文子序列
516. 最長回文子序列
給你一個字元串 s ,找出其中最長的回文子序列,并傳回該序列的長度。
子序列定義為:不改變剩餘字元順序的情況下,删除某些字元或者不删除任何字元形成的一個序列。
示例 1:
輸入:s = "bbbab"
輸出:4
解釋:一個可能的最長回文子序列為 "bbbb" 。
示例 2:
輸入:s = "cbbd"
輸出:2
解釋:一個可能的最長回文子序列為 "bb" 。
提示:
1 <= s.length <= 1000
s 僅由小寫英文字母組成
題解:
用
dp[i][j
表示字元串 s 下标範圍
[i, j]
内最長回文子序列的長度,假設字元串 s 的長度為 n,則隻有當
0<=i<j<n
時,才會有
dp[i][j] > 0
,否則有
dp[i][j]=0
class Solution:
def longestPalindromeSubseq(self, s: str) -> int:
n = len(s)
dp = [[0] * n for _ in range(n)]
# 倒序遞歸
for i in range(n-1, -1, -1):
# bad case,若隻有一個字元,最長回文子序列長度是 1,dp[i][j] = 1 (i == j)
dp[i][i] = 1
for j in range(i+1, n):
# 它倆一定在最長回文子序列中
if s[i] == s[j]:
dp[i][j] = dp[i+1][j-1] + 2
else:
# s[i+1..j] 和 s[i..j-1] 誰的回文子序列更長
dp[i][j] = max(dp[i+1][j], dp[i][j-1])
return dp[0][n-1]
參考:子序列問題通用思路|最長回文子序列
9. 最長回文子串
5. 最長回文子串
給你一個字元串 s,找到 s 中最長的回文子串。
示例 1:
輸入:s = "babad"
輸出:"bab"
解釋:"aba" 同樣是符合題意的答案。
示例 2:
輸入:s = "cbbd"
輸出:"bb"
提示:
1 <= s.length <= 1000
s 僅由數字和英文字母組成
題解:
class Solution:
def longestPalindrome(self, s: str) -> str:
long_sub = ""
for i in range(len(s)):
odd = self.is_palindrom(s, i, i) # 回文串元素個數為奇數
even = self.is_palindrom(s, i, i + 1) # 回文串元素個數為偶數
long_sub = odd if len(odd) > len(long_sub) else long_sub
long_sub = even if len(even) > len(long_sub) else long_sub
return long_sub
def is_palindrom(self, s, l, r):
"""不超出邊界且擴散的兩邊的元素相等,傳回回文子串"""
while l >= 0 and r < len(s) and s[l] == s[r]:
l -= 1
r += 1
return s[l + 1: r]
s = 'babad' n = len(s) = 5
i = 0
奇數:l = 0, r = 0 ==> s[l] == s[r] ==> l = -1, r = 1 ===> s[0: 1] ==> long_sub = "b"
偶數: l = 0, r = 1 ==> s[l] != s[r] ===> s[0: 1] ==> long_sub = "b"
i = 1
奇數:l = 1, r = 1 ==> s[l] == s[r] ==> l = 0, r = 2 ===> l = -1, r = 3 ===> s[0: 3] ==> long_sub = "bab"
偶數: l = 1, r = 2 ==> s[l] != s[r] ===> s[2: 2] ==> long_sub = "bab"
....