模式識别課分為“分類”和“回歸”
分類:輸出量是離散的類别表達
回歸:輸出量是連續的信号表達(回歸值)
回歸是分類的基礎:離散的類别值是由回歸值做判斷決策的得到的
模式識别:根據已有得知識表達,針對待識别模式,決策其所屬的類别或預測其對應的回歸值
數學解釋:模式識别可以看做一種函數映射,将待識别模式從輸入空間映射到輸出空間,函數是關于已有知識的表達。
特征提取,從原始輸入資料提取更有效的資訊。
回歸器:将特征映射到回歸值。
模型(廣義):特征提取+回歸器+判别函數
模型(狹義):特征提取+回歸器
分類器:回歸器+判别函數
魯棒性:針對不同的觀測條件,仍能夠有效的表達類别之間的差異。
特征向量:多個特征構成的(列)向量
特征向量的歐式距離:表征兩個向量之間的相似程度
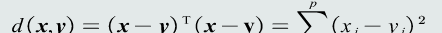
線性模型:
Over-determined:訓練樣本個數>>模型參數個數,額外添加一個标準,通過優化該标準倆确定一個近似解,該标準稱作目标還是或者代價函數又或者損失函數。
目标函數以待學習的模型參數作為自變量,以訓練樣本作為給定量
監督式學習:訓練樣本及輸出真值都給定情況下的機器學習算法
通常用最小化訓練誤差作為目标函數進行優化
無監督式學習:隻給定訓練樣本,沒有給定輸出真值情況下的機器學習算法。
根據樣本間的相似程度來進行決策
典型應用:聚類,圖像分割
半監督式學習:既有标注的樣本,也有未标注的樣本
典型應用:網絡流資料
強化學習:機器自行探索決策、真值滞後回報的過程
定義從輸入狀态到動作決策為一個政策
使用該政策進行決策時,給予每次決策一個獎勵
累積多次獎勵獲得回報值
回報的期望值作為該政策的價值函數
通過最大值回報的期望值,解出該政策的參數
測試集和訓練集是互斥的,但假設同分布
測試誤差,模型在測試集上的誤差,反映了模型的泛化能力,,也稱泛化誤差
泛化能力:訓練得到得模型不僅要對訓練樣本具有決策能力,也要對新的模式具有決策能力
過拟合:模型過于拟合訓練資料
提高泛化能力:選擇複雜度适合的模型;正則化,在目标函數中加入正則項
多項式拟合:
超參數M多項式的階數,決定了模型的複雜度
超參數N訓練樣本的個數
超參數調節:從訓練集中劃分出一個驗證集,基于驗證集調節超參數
留出法:
1、 随機劃分:将資料集分為兩組:訓練集和測試集。利用訓練集訓練模型,然後利用測試集評估模型的量化名額。
2、 取統計值:為了可分單次随機劃分代理的偏差,将上述随機劃分進行若幹次,取量化名額的平均值(以及方差、最大值等)最為最終的性能量化評估結果。
K折交叉驗證:
将資料集分割成k個子集,從中選取當個子集作為測試集,其餘的作為訓練集。
交叉驗證重複k次,使得每個子集都被測試一次,将k次的評估值取平均,作為最終的量化評估結果。
留一驗證:
每次隻取一個樣本作為測試集,其餘作為訓練集。
等同于k為樣本個數的k折交叉驗證
真陽性TP:真值為正,預測為正
假陽性FP:真值為負,預測為正
真陰性TN:真值為負,預測為負
假陰性FN:真值為正,預測為負
準确度:(TP+TN)/(TP+FP+TN+FN) 陽性和陰性樣本比例失衡難度量性能
精度precision:TP/(TP+FP)
召回率recall:TP/(TP+FN)
F-Score: F=[(a2+1)*p*r]/(a2pr)
混淆矩陣:列代表預測值,行代表真值。對角線元素值越大代表模型性能越好。
PR曲線:橫軸:召回率;縱軸:精度 曲線越右上凸,性能越好
ROC曲線:橫軸FPR=FP/(FP+TN);縱軸召回率
曲線下方面積AUC,AUC=1完美分類器,AUC=0.5随機猜測
MED分類器:
最近鄰:取與測試樣本最近的一個訓練樣本作為測試的原型。
缺點:對類的表達誤差較大,對噪聲和異常樣本比較敏感
距離度量的标準:同一性,非負性,對稱性,三角不等式
常用的幾種距離度量
MED分類器:最小歐式距離分類器,距離度量:歐式距離,類原型:均值
沒有考慮特征變化的不同及特征之間的相關性
協方差矩陣:對角元素不相等:每維特征的變化不同;非對角元素不為0:特征之間存在相關性
特征白化:将原始特征映射到一個新的特征空間,使得在新空間中特征的協方差矩陣為機關矩陣,進而去除特征變化的不同及特征之間的相關性
解耦:實作協方差矩陣對角化,去除特征的相關性
白化:進行尺度變化,實作所有特征具有相同方差
馬氏距離:距離度量:馬氏距離;類原型:均值
缺點:均值一樣時會選擇方差較大的類
貝葉斯分類:
後驗機率:
MAP分類器:将測試樣本決策分類給後驗機率大的那個類
損失:錯誤決策所對應的懲罰量,可以手動設定也可以訓練得到
貝葉斯分類器:在MAP的基礎上,加上決策風險因素
樸素貝葉斯分類器:假設特征之間互相獨立
拒絕選項:當後驗機率小于門檻值時,分類器可以拒絕
門檻值等于1,所有樣本都拒絕,門檻值小于1/k,所有樣本都不會被拒絕
似然函數:
先驗機率的似然函數:
先驗機率的最大似然估計即該類訓練樣本出現的機率
觀測似然機率的似然函數(高斯分布的情況):
高斯分布均值的最大似然估計即樣本的均值
高斯分布協方差的最大似然估計等于所有訓練模式的協方差
均值最大似然估計是無偏估計,協方差的最大似然估計是有偏估計
協方差的修正:
貝葉斯估計:給定參數分布的先驗機率及樣本,估計參數分布的後驗機率
參數的後驗機率:
高斯觀測似然:
先驗機率:
後驗機率
參數的後驗機率是高斯分布
樣本數足夠大時,樣本均值就是參數的無偏估計
貝葉斯估計:把參數看作是參數空間的一個機率分布,依賴訓練樣本來估計參數的後驗機率,進而得到觀測似然關于參數的邊緣機率。
最大似然估計:把參數看做是确定值
KNN估計:
K個樣本落在區域R内的機率密度可用二項分布表達:
當N很大時,二項分布的均值約等于k
是以
K鄰近:給定x找到其對應的區域,使得包含k個訓練樣本
優點:可以自适應确定x相關的區域R的範圍
缺點:不是連續函數;不是真正的機率表達,機率密度函數的積分不為1;易受噪音影響
;推理測試階段仍需存儲所有樣本
直方圖估計:
區域R的确定:直接将特征空間分為m個格子,每個格子即為一個區域R,即區域的位置固定;平均分格子大小,是以每個格子體積V=h,即區域的大小固定;相鄰格子不重疊;落到格子裡的訓練樣本個數不定。
機率密度估計:先判斷落到哪個格子,機率密度即為該格子的統計值
優點:固定區域,減少噪聲影響;不需要存儲訓練樣本
缺點:固定區域R的位置,若x落在兩格子交界區域,意味着目前格子不是以x為中心,導緻估計不準确;固定區域R的大小,缺乏自适應能力
雙線性插值:針對自适應不強的問題
a,b代表x到兩均值的距離
帶寬h過小,機率密度函數過于尖銳,反之,過于平滑
核密度估計:
區域R的确定:以x為中心,固定帶寬h
核函數需滿足以下條件:
核函數必須是對稱的函數
優點:自适應确定R的位置;使用所有訓練樣本,克服噪聲影響;若核函數連續,機率密度函數也連續
缺點:需要存儲所有訓練樣本
生成模型:給定訓練樣本,直接在輸入空間内學習其機率密度函數
優勢:可以根據機率密度函數采樣新的樣本;可以檢測出較低機率的資料,實作離群點檢測
劣勢:高維的x需要大量訓練樣本
判别模型:給定訓練樣本,直接在輸入空間内估計後驗機率
優勢:快速直接,省去了耗時的高維觀測似然機率估計
線性判據:
w決定決策邊界的方向
w0決定決策邊界的偏移量,是兩類輸出值分别為正負
訓練樣本遠遠大于參數個數,是以解不唯一
解域:在參數空間内,參數的所有可能解所處的範圍
目标函數:
加入限制條件,提高泛化能力
并行感覺機:
串行感覺機:
如果樣本線性可分,感覺機算法收斂于一個解
步長決定收斂速度及是否收斂到全局最優
提高泛化能力:加入margin限制條件
Fisher線性判據:
線性判據模型可以看作将原空間上的點x投影到新的空間y
不同樣本類别差異盡量大,類内樣本分布離散程度盡量小
類間樣本差異程度:用兩類樣本分布的均值之差度量
類内樣本離散程度:用每類樣本分布的協方差矩表征
支援向量機:
間隔:兩個類的訓練樣本中找到距離決策邊界最近的訓練樣本,記作x+和x-
x+和x-到決策邊界的垂直距離叫做間隔,記為d+和d-
平行決策邊界且經過x+和x-的兩個超平面稱為間隔邊界
位于間隔邊界的兩個樣本稱為支援向量
對偶問題:
支援向量機算法: