機器學習第二次作業

預習筆記

第一章

• 主要内容
  • 模式識别和機器學習的基本概念
  • 模型的概念群組成
  • 特征向量的定義與計算
• 模式識别的基本概念與應用
• 機器學習的基本概念
  • 監督式學習，無監督式學習，半監督式學習，強化學習
  • 模型訓練中存在的問題
    • 樣本稀疏、不均勻、帶有噪聲
  • 模型泛化問題
    • 選擇複雜度合适的模型
    • 正則化
  • 過拟合現象
  • 模型評估方法
    • 留出法、留一法、K折交叉驗證
  • 模型性能度量
    • TP/FP/FN/TN
    • 準确度Accuracy、精度Precision、召回率Recall、特異度Specificity、F-Score
    • 混淆矩陣
    • PR曲線
    • ROC曲線

第二章

• • 基于距離的分類器
    • 歐氏距離、權重歐式距離、曼哈頓距離、馬氏距離
    • 将樣本到每個類的距離作為決策模型，把測式樣本判定為與其距離最近的類
  • 特征白化
• MED分類器（最小歐氏距離分類器）
  • 以歐氏距離為度量
  • 以均值為類的原型
  • 隻考慮到類原型的距離，不考慮類樣本的分布，存在分類不合理的問題
• • 将原始特征映射到新的一個特征空間，使得在新空間中特征的協方差為機關矩陣，進而去除特征變化的不同及特征之間的相關性
  • 特征解耦：先去除特征之間的相關性
  • 特征白化：在解耦的基礎上再對特征進行尺度變化
• 馬氏距離
  • 表示資料的協方差距離，是一種有效的計算兩個未知樣本集的相似度的方法
• MICD分類器（最小類内距離分類器）
  • 以馬氏距離為度量
  • 會選擇方差較大的類

第三章

• • 貝葉斯決策和學習
• MAP分類器（最大後驗機率分類器）
  • 将測試樣本分類到後驗機率最大的類
  • 先驗機率：指根據以往經驗和分析得到的機率
  • 後驗機率：指在得到結果的資訊後重新修正的機率，通過Bayes定理，用先驗機率和似然函數計算出來
  • 決策産生的誤差用機率誤差表達，是未選擇的類對應的後驗機率
• 貝葉斯分類器
  • 在MAP分類器的基礎上，加入決策風險因素
• 參數估計方法
  • 極大似然估計
    • 利用已知的樣本結果，反推最有可能導緻結果的參數值
  • 貝葉斯估計
    • 已知樣本滿足某種未知參數的機率分布，把待估計參數看作符合先驗機率分布的随機變量。對樣本進行觀測的過程就是把先驗機率密度轉化為後驗機率密度，利用樣本資訊修正了對參數的初始估計值。
• 無參數估計方法
  • KNN估計
  • 直方圖估計
  • 核密度估計
    • 利用平滑的峰值函數來拟合觀察到的資料，進而模拟真實的機率分布曲線

第四章

• • 線性判定與回歸
• 生成模型
  • 給定訓練樣本，直接在輸入空間内學習其機率密度函數p(x)
  • 優勢是可以根據p(x)采樣新的樣本資料，可以測驗出較低機率的資料，實作離群點檢測。
  • 劣勢是高維的x需要大量訓練樣本才能準确估計p(x)，否則會出現次元災難
• 判别模型
  • 給定訓練樣本，直接在輸入空間内估計後驗機率，快速直接，省去了耗時的高維觀測似然估計
• 線性判據
  • 如果判别模型f(x)是線性函數，則f(x)是線性判據
• 感覺機算法
  • 根據标記過的訓練樣本學習模型參數
  • 并行感覺機與串行感覺機
• Fisher線性判據
  • 找到最合适的投影軸，使兩類樣本在該軸上投影的重疊部分最少，進而使分來效果達到最佳
• 支援向量機
  • 給定一組訓練樣本，使得兩個類中與決策邊界最近的訓練樣本到決策邊界之間的距離最大
• 拉格朗日對偶問題

複習筆記

• 模式識别的概念

  

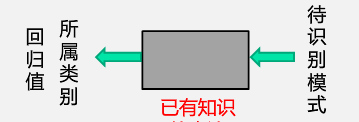
  • 模式識别的基本定義是根據已有知識的表達， 針對待識别模式，判别決策其所屬的類别或者預測其對應的回歸值，本質上是一種推理過程。模式識别在數學解釋上可以看作一種函數映射f(x)，是關于已有知識的一種表達方式，也可以稱作模型，狹義的模型由特征提取和回歸器組成的。
  • 模式識别的任務形式有分類和回歸，前者的輸出量是輸出量是離散的類别表達，後者則是單個或多個次元連續的信号表達（即回歸值）。回歸是分類的基礎，離散的類别值是由回歸值做判别決策得到的，是以分類器是由回歸器與判别函數構成，其加上特征提取則構成廣義的模型。
• 模型的組成
  • 特征提取：指從原始輸入資料提取出更有效的資訊
  • 回歸器：将特征映射到回歸值
  • 模型（廣義）= 特征提取 + 回歸器 + 判别函數
  • 模型（狹義）= 特征提取 + 回歸器
  • 分類器 = 回歸器 + 判别函數
  • 判别器可以是二類分類和多類分類，前者根據回歸值的正負來确定分類，後者根據最大值來确定分類
  • 判别函數通常已知固定，是以不能當作模型的一部分

  • 

• 特征的概念
  • 可以用于區分不同類别模式的、可測量的量
  • 具有辨識能力：提升不同類别之間的識别性能
  • 魯棒性：針對不同的觀測條件，仍能夠有效表達類别之間的差異性
  • 特征向量：指多個特征構成的（列）向量，長度為向量的模，方向為特征向量除其模長
  • 特征空間：每個坐标軸表示一個特征，空間中和坐标原點相連的向量代表着該模式的特征向量
• 特征向量相似度度量
  • 特征向量投影

    

    向量x到向量y的投影是向量x垂直投射到向量y方向上的長度，是個标量。投影的含義是向量x分解到向量y方向上的長度，投影長度越大，說明兩個向量方向上越相似
  • 殘差向量

    

  • 歐式距離

    

    • 兩個特征向量的歐式距離可以表示兩個向量間的相似程度，綜合考慮了方向和模長
  • 餘弦相似度

    

    隻考慮方向，不考慮模長
• • 很顯然想要進行模式識别離不開模型，想要确定模型，就需要先設計好模型結構，然後由機器學習通過訓練樣本得到模型參數

  

• 機器學習的分類
  • 監督式學習
    • 訓練樣本及其輸出真值都給定情況下的機器學習，是最常見的學習方式
    • 監督式學習問題可以進一步被分為回歸和分類問題
    • 通常使用最小化訓練誤差作為目标函數進行優化
  • 無監督式學習
    • 隻給定訓練樣本、沒有給輸出真值情況下的機器學習算法，難度遠高于監督式學習
    • 無監督式學習的目标是對資料中潛在的結構和分布模組化，以便對資料作更進一步的學習。
    • 通常根據訓練樣本之間的相似程度來進行決策，典型應用有聚類和圖像分割
  • 半監督式學習
    • 既有标注的訓練樣本、又有未标注的訓練樣本情況下的學習算法

    • 半監督式學習問題介于監督式和非監督式學習之間。

      許多現實中的機器學習問題都可以歸納為這一類。因為對資料加上标注耗時耗力，對于非專業人士也有一定的阻礙。而無标注資料的收集存儲都是極為友善的

    • 可以看作有限制條件的無監督式學習問題，即标注過的訓練樣本用作限制條件，典型應用有網絡流資料
  • 強化學習
    • 真值滞後回報的過程，适用于累積多次決策動作才能知道最終結果好壞，很難針對單次決策給出對應的真值的任務，例如棋類遊戲。
• 模型的泛化能力
  • 泛化能力是指訓練得到的模型不僅要對訓練樣本要具有決策能力，還要對新的模式具有決策能力。
  • 訓練樣本存在的一些問題
    • 訓練樣本稀疏：給定的訓練樣本數量是有限的，很難完整表達樣本的真實分布
    • 訓練樣本采樣過程可能不均勻：有些區域采樣密一些，有些區域采樣疏一些
    • 一些樣本可能帶有噪聲
• • 模型訓練階段表現很好，但是在測試階段表現差

    

• 如何提高泛化能力
  • 選擇複雜度适合的模型：模型選擇
  • 正則化：在目标函數中加入正則項

    

• 評估方法與性能名額
  • 留出法
    • 直接将資料集D劃分為兩個互斥的部分，其中一部分作為訓練集，另一部分用作測試集
    • 通常訓練集和測試集的比例為70%：30%。
    • 資料集的劃分要注意盡可能保持資料分布的一緻性，避免因資料劃分過程引入的額外偏差而對最終結果産生影響。在分類任務中，保留類别比例的采樣方法稱為分層采樣
    • 同時要注意采用若幹次随機劃分避免單次使用留出法的不穩定性。
  • K折交叉驗證法
    • 交叉驗證法先将資料集劃分為K個大小相似的互斥子集，每次采用K−1個子集的并集作為訓練集，剩下的那個子集作為測試集。進行K次訓練和測試，最終傳回K個測試結果的均值

      

  • 留一法
    • 留一法是K折交叉驗證K=樣本數時候的特殊情況。即每次隻用一個樣本作測試集，其它所有樣本來訓練，計算開銷較大
• 性能度量
  • 根據預測正确與否，将樣例分為以下四種：
    • True positive(TP): 真正例，将正類正确預測為正類數
    • False positive(FP): 假正例，将負類錯誤預測為正類數
    • False negative(FN):假負例，将正類錯誤預測為負類數
    • True negative(TN): 真負例，将負類正确預測為負類數。
  • 準确度Accuracy

    

  • 精度Precision

    

  • 召回率Recall

    

  • 特異度Specificity

    

  • F-Score

    

    • F1-Score
      • F-Score設定a=1

        

• • 行為真值，列為預測值，元素為計數統計值
  • 對角線的值越大，表示模型性能越好
• • 橫軸為召回率，縱軸為精度
  • 對各類别樣本分布敏感
  • 越往右上凸突性能越好
• • 橫軸為假陽性比例（FPR），縱軸為召回率
  • FPR = 1 - Specificity
  • 對各類别樣本分布不敏感
  • 越往左上凸突性能越好
  • 對角線為随機識别算法的性能
  • 可使用曲線下面積（AUC）度量，其中AUC = 0.5時為随機識别算法

• • 把樣本到每個類的距離作為決策模型，将測試樣本判定為與其距離最近的類
• 常見的幾種距離度量
  • 歐氏距離

    

  • 曼哈頓距離(Manhattan Distance)

    

  • 權重歐式距離
    • 對每維特征設定不同的權重

  • 

• • 二類MED分類器決策邊界

    

    • 在高維空間中，該決策邊界是一個超平面，垂直平分兩個類原型的線

  • 存在的問題

    C1 = {(5, 4), (7, 0), (3.5, 1), (4.5, 3)}

    C2 = {(4, 4), (8, 5), (8, 3), (12, 4)}

    判斷y = (4,5)所屬類别

    

    根據MED決策方程，y屬于C1類，但直覺上y更接近于C2類。因為MED分類器沒有考慮特征變化的不同以及特征之間的相關性。
• • 目标
    • 特征之間存在相關性和尺度不同的問題
  • 解耦
    • 通過W1實作協方差矩陣對角化，去除特征之間的相關性
    • 解耦後歐式距離不變
  • 白化
    • 通過W2對上一步變換後的特征再進行尺度變換實作所有特征具有相同方差
  • 過程

    

    

    

    

• MICD分類器（最小馬氏距離分類器）
  • 二類MICD分類器決策邊界

    

    

  • • 誇大了變化微小的變量的作用
    • 受協方差矩陣不穩定的影響，馬氏距離并不總是能順利計算出
    • 在均值相同時，MICD分類器會選擇方差較大的類

      

  • 馬氏距離的優點
    • 不受量綱的影響，兩點之間的馬氏距離與原始資料的測量機關無關
    • 由标準化資料和中心化資料（即原始資料與均值之差）計算出的二點之間的馬氏距離相同
    • 馬氏距離可以排除變量之間的相關性的幹擾，綜合考慮了類的不同特征之間的相關性和尺度差異

      

• 貝葉斯規則
  • 

• • 二分類決策邊界
  • 平均機率誤差
  • 決策目标
    • 最小環機率誤差
• • 決策風險和損失

    

    

  • • 選擇決策風險最小的類。即對于所有測試樣本，選擇損失最小的類，以達到期望損失最小
    • 期望損失，即所有樣本的決策損失之和
  • 樸素貝葉斯分類器
    • 如果特征是多元，學習特征之間的相關性會很困難

      

• • 最大似然估計

    • 

  • 先驗機率估計

    

    先驗機率的最大似然估計就是該類訓練樣本出現的頻率
  • 觀測機率估計：高斯分布

    

    

  • 均值估計
    • 無偏估計

      

    • 高斯分布均值的最大似然估計等于樣本的均值

      

  • 協方差估計
    • 有偏估計

      

    • 高斯分布協方差的最大似然估計等于所有訓練模式的協方差

      

    • 協方差估計的修正

      

  • • 已知樣本滿足某種未知參數的機率分布，把待估計參數看作符合先驗機率分布的随機變量。對樣本進行觀測的過程就是把先驗機率密度轉化為後驗機率密度，利用樣本資訊修正了對參數的初始估計值
    • 參數的後驗機率

      

    • 貝葉斯估計：高斯觀測似然

      

      • 參數（高斯均值）先驗機率

        

      • 參數（高斯均值）後驗機率

        

        

        

      • 分析
        • 當𝑁𝑖足夠大時， 樣本均值m就是參數θ的無偏估計

        

        • 參數先驗對後驗的影響

          

    • 貝葉斯估計：不斷學習能力
      • 允許最初的、基于少量訓練樣本的、不太準的估計
      • 随着訓練樣本的不斷增加，可以串行的不斷修正參數的估計值，進而達到該參數的期望真值
    • 流程

      

    • 貝葉斯估計一般比最大似然估計複雜，但能力也更強

• • 

    • 優點
      • 可以自适應的确定𝒙相關的區域𝑅的範圍
    • 缺點
      • KNN機率密度估計不是連續函數
      • 不是真正的機率密度表達，機率密度函數積分是 ∞ 而不是1。例如，在k=1時

  • 

    

    • • 固定區域𝑅：減少由于噪聲污染造成的估計誤差
      • 不需要存儲訓練樣本
    • • 固定區域𝑅的位置：如果模式𝒙落在相鄰格子的交界區域，意味着目前格子不是以模式𝒙為中心，導緻統計和機率估計不準确
      • 固定區域𝑅的大小：缺乏機率估計的自适應能力，導緻過于尖銳或平滑
    • 雙線性插值

      

    • 帶寬選擇

      

  • • 以任意待估計模式𝒙為中心、固定帶寬ℎ，以此确定一個區域𝑅
    • 原理

      

    • 機率密度估計

      

    • 核函數

      

    • • 以待估計模式𝒙為中心、自适應确定區域𝑅的位置（類似KNN）
      • 使用所有訓練樣本，而不是基于第 𝑘 個近鄰點來估計機率密度，進而克服KNN估計存在的噪聲影響
      • 如果核函數是連續，則估計的機率密度函數也是連續的
    • • 與直方圖估計相比， 核密度估計不提前根據訓練樣本估計每個格子的統計值，是以它必須要存儲所有訓練樣本
    • • 帶寬ℎ決定了估計機率的平滑程度
      • 因為給定的訓練樣本數量是有限的，是以要求根據這些訓練樣本估計出來的機率分布既能夠符合這些訓練樣本，同時也要有一定預測能力，即也能估計未看見的模式

• • 優勢
    • 可以根據p(x)采樣新的樣本資料，可以測驗出較低機率的資料，實作離群點檢測。
  • 劣勢
    • 高維的x需要大量訓練樣本才能準确估計p(x)，否則會出現次元災難
• • 給定訓練樣本，直接在輸入空間内估計後驗機率
  • • 快速直接，省去了耗時的高維觀測似然估計
• • 可以用于二類分類，決策邊界是線性的
  • 也可以用于多類分類，相鄰兩類之間的決策邊界也是線性的
  • • 計算量少：在學習和分類過程中，線性判據方法都比基于學習機率分布的方法計算量少
    • 适用于訓練樣本較少的情況
  • 數學表達

    

  • w的方向

    

  • w0的作用
  • 任意樣本到決策邊界的距離r r的絕對值可以作為confidence score：值越大，這個點屬于正類或者負類的程度越大，𝑓(𝒙)是樣本𝒙到決策面𝐻的代數距離度量
  • 學習方法

    

    

    

• • 預處理

    

  • 目标函數

    

  • 并行感覺機
    • 訓練樣本并行給出
    • • 對所有被錯誤分類的訓練樣本，其輸出值取反求和

        

        

      • 偏導不含有a，不能通過令偏導為0來求a
  • 梯度下降算法

    

    步長用來調整更新的幅度，每次疊代可以用不同的步長

    參數更新

  • 參數a的更新公式（梯度下降算法）

    

    帶入并行感覺機的梯度公式：

    

  • 串行感覺機算法
    • 訓練樣本是串行給出的

    • 

      

      

    • 算法流程

      

  • 收斂性
    • 如果訓練樣本是線性可分的，感覺機算法理論上收斂于一個解
    • 這隻是保證算法會停止，但是最終結果不一定是全局最優

    • 

• • 投影後，使得不同類别的樣本分布的類間差異盡可能大，同時使得各自類内樣本分布的離散程度盡可能小
  • 類間樣本的差異程度
    • 用兩類樣本分布的均值之差度量
  • 類内樣本的離散程度
    • 用每類樣本分布的協方差矩陣表征
• • 最大化總間隔
• • 在數學最優問題中，是一種尋找變量受一個或多個條件所限制的多元函數的極值的方法
  • KKT條件
    • 是解決最優化問題的時用到的一種方法。這裡提到的最優化問題通常是指對于給定的某一函數，求其在指定作用域上的全局最小值
  • 設d∗是拉格朗日對偶問題的最優解，則不管原問題是不是凸優化問題，都一定有d∗=f∗則強對偶成立。這時對偶函數是原問題的緊緻下界

  • 

    則弱對偶成立
  • 能不能取到強對偶條件取決于目标函數和限制條件的性質。如果滿足原問題是凸優化問題，并且至少存在一個絕對可行點，那麼就具有強對偶性

學習心得與總結

• 機器學習是計算機及其應用領域的一門重要學科。通過這學期的課程學習，大概了解了機器學習的一些基本方法，特别是監督式學習方法，如感覺機、K近鄰法、貝葉斯法、支援向量機等。
• 總體來說這門課雖然是介紹性的入門課程，但還是由淺入深的。通過闡明思路以及給出必要數學推導的方法，結合部分具體問題和執行個體，為進一步學習機器學習知識打下基礎。
• 當然，這門課因為對于數學、特别是線性代數和機率論的高要求，需要對之前學習過的内容做一些概念性的整合。其實課程中介紹的很多方法還是缺少例子的，難以有整體性的了解，如果概念還不清晰就更緻命了。确實需要實踐環節來加深印象，可是從理論到實踐跳的有點太快了，這方面的引導可能由于不可抗力比較缺乏吧。