洛谷題目傳送門
閑話
看完洛谷larryzhong巨佬的題解,蒟蒻一臉懵逼
如果哪年NOI(放心我這樣的蒟蒻是去不了的)又來個決策單調性優化DP,那蒟蒻是不是會看都看不出來直接爆\(0\)?!
還是要想點辦法,不失一般性也能快捷地判定決策單調。
對于判定決策單調的分析
再補一句決策單調性的概念:狀态轉移方程形如\(f_i=\min/\max_{j=1}^{i-1} g_j+w_{i,j}\),且記\(f_i\)的最優決策點為\(p_i\)(也就是\(f_i\)從\(g_{p_i}+w_{i,p_i}\)處轉移最優)若滿足\(p_i\le p_{i+1}\),則該方程滿足決策單調性。(摘自蒟蒻的DP優化總結)
顯然每個決策\(j\)可以用一個關于\(i\)的函數\(f_j(i)\)表示。
函數的一個重要思想:數形結合!
光靠腦子想不到規律,隻好先舉一些用語言難以描述的反例。我們的函數不能這樣
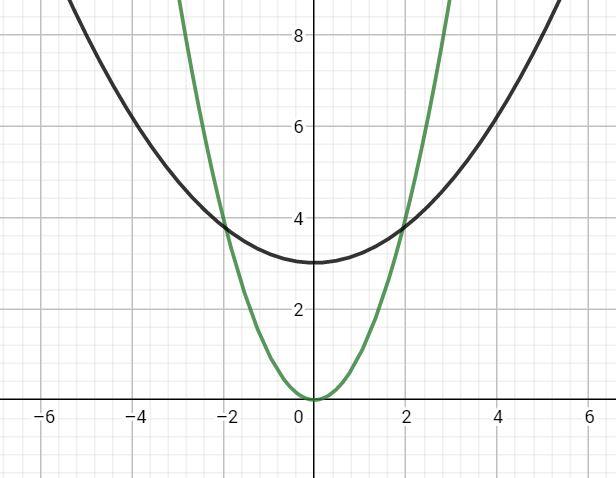
看到這裡Dalao們有沒有一點想法呢?蒟蒻反正想到了一點——兩個函數必須隻有一個交點!在這一點之前一個函數更優,而之後就被永遠取代了。
感覺滿足條件的函數其實很少,分類讨論一下(如有誤歡迎Dalao指教)
直線
顯然上面的基本要求都滿足。不過要是函數是直線的話都可以用斜率優化搞了(\(k_1x+b_1\ge k_2x+b_2,x\ge\frac{b_2-b_1}{k_1-k_2}\))。
不是直線
為了避免圖1的尴尬情況,可能需要所有決策函數之間可以通過平移互相變換(形如\(f_j(x)=f_k(x-a)+b\))。
為了避免圖2的尴尬情況,可能需要函數的導函數在各自的定義域内單調遞增/遞減(注意是導函數不是原函數)。
接着,根據蒟蒻肝過的幾個題,好像還有一條規律——
如果導函數遞增、求最大值(檸檬),或者導函數遞減、求最小值,要用單調棧。
如果導函數遞增、求最小值(本題),或者導函數遞減、求最大值(Lightning Conductor),要用單調隊列。
複雜的函數
蒟蒻見過這一道(Yet another minimization problem)
感覺可以看成對于每一種數都有一個函數\(\frac{(c_i-c_j)(c_i-c_j+1)}{2}\),單看這一個是滿足決策單調性的(\(c_i\ge c_j\),定義域内的導函數是遞增的)。
那麼總函數就可以寫成\(f_j(i)=g_j+\sum\frac{(c_i-c_j)(c_i-c_j+1)}{2}\),怎麼看也不像是不滿足決策單調性的。
本題的思路
那麼就可以回歸本題了。
設\(len_i\)為第\(i\)句的長度,\(s_i=i+\sum\limits_{j=1}^i len_j\)(加上\(i\)是預設一句話後面有空格)
設\(f_i\)為選前\(i\)句的最小代價,我們枚舉目前這一行填入最後面的多少個句子,注意行末沒有空格,長度要\(-1\),那麼有方程
\[f_i=\min\limits_{j=0}^{i-1}\{f_j+|s_i-s_j-1-L|^P\}
\]
容易發現後面這一坨決策函數是關于直線\(x=s_j+1+L\)對稱的。把它去絕對值,變成兩段,顯然左邊一段和右邊一段的導函數都是遞增的,左邊恒\(<0\),右邊恒\(>0\)。又因為這函數是連續的,是以當然整個函數的導函數也單調遞增咯!
用隊列維護決策二分棧的過程不再贅述,總結裡也有。時間複雜度\(O(Tn\log n)\)
看到Dalao們都記錄了一個三元組,可蒟蒻還是覺得沒啥必要啊。。。隻要儲存隊列中相鄰兩個元素的臨界值\(k\)就好了吧。
一個寫法技巧:
二分決策\(x,y(x<y)\)的臨界值的時候,左端點設成\(x\)就好了,沒必要設成\(1\)(難怪蒟蒻之前寫Lightning Conductor跑得有點慢)
三個坑點:
不管是轉移還是輸出,都要去掉行末的空格(怪蒟蒻看題不清)
當答案大于\(10^{18}\)的時候開longlong也炸了,是以要用實數以犧牲精度的代價換來更大的值域。然而double真的WA了。于是要開long double。
cmath的pow太慢了容易TLE,要手寫快速幂。
#include<cstdio>
#include<cmath>
#include<cstring>
#define RG register
#define R RG int
#define G c=getchar()
#define Calc(i,j) f[j]+qpow(abs(s[i]-s[j]-L))//計算函數值
using namespace std;
typedef long double LD;//開long double
const int N=1e5+9;
int n,L,P,s[N],q[N],k[N],pr[N];
LD f[N];
char str[N][33];
inline int in(){
RG char G;
while(c<'-')G;
R x=c&15;G;
while(c>'-')x*=10,x+=c&15,G;
return x;
}
inline LD qpow(RG LD b){//自己寫快速幂
RG LD a=1;
for(R k=P;k;k>>=1,b*=b)
if(k&1)a*=b;
return a;
}
inline int bound(R x,R y){//二分臨界值
R l=x,r=n+1,m;//左端點設為x減小常數
while(l<r){
m=(l+r)>>1;
Calc(m,x)>=Calc(m,y)?r=m:l=m+1;
}
return l;
}
int main(){
R T=in(),i,h,t;
while(T--){
n=in();L=in()+1;P=in();//把L處理了一下
for(i=1;i<=n;++i){
if(scanf("%s",str[i]));
s[i]=s[i-1]+strlen(str[i])+1;//記字首和
}
for(q[i=h=t=1]=0;i<=n;++i){
while(h<t&&k[h]<=i)++h;
f[i]=Calc(i,q[h]);pr[i]=q[h];//記錄轉移位置友善輸出方案
while(h<t&&k[t-1]>=bound(q[t],i))--t;
k[t]=bound(q[t],i);q[++t]=i;
}
if(f[n]>1e18)puts("Too hard to arrange");
else{
printf("%.0Lf\n",f[n]);
for(q[t=0]=i=n;i;q[++t]=i=pr[i]);
for(;t;--t){
for(i=q[t]+1;i<q[t-1];++i)
printf("%s ",str[i]);
puts(str[i]);//行末不要搞空格
}
}
puts("--------------------");
}
return 0;
}