字首和優化
當DP過程中需要反複從一個求和式轉移的話,可以先把它預處理一下。運算一般都要滿足可減性。
比較naive就不展開了。
題目
【Todo】洛谷P2513 [HAOI2009]逆序對數列
【Done】洛谷P2511 [HAOI2008]木棍分割
【Done】洛谷P4099 [HEOI2013]SAO
【Done】NOIAC37 染色
單調隊列優化
前置技能:單調隊列(經典的問題模型:洛谷P1886 滑動視窗)
用于優化形如\(f_i=\min/\max_{j=l_i}^{i-1}\{g_j\}+w_i\),且滿足\(l_i\le l_{i+1}\)的轉移。
人話:對于序列中的每個點,從其左側一段決策區間内的最值進行轉移,且決策區間随着序列下标的增大也不斷右移(就像視窗向右滑動)。
設\(j<k\),容易發現如果\(g_j\)劣于\(g_k\)的話,那麼當決策區間移動到\(k\)以後,\(j\)永遠不會成為最優決策點,再也不會被轉移了。
于是,我們隻要維護一個隊列,滿足下标遞增,決策性遞減。我們需要目前的隊首成為最優決策點,那麼當隊首第一次超出了區間範圍(以後也就永遠超出了)就把它出隊。為了保證單調性,隊尾新加入點之前,要先把隊列中比它劣的點依次從隊尾出隊。
【Sol.】洛谷P1776 寶物篩選_NOI導刊2010提高(02)(就是多重背包)
【Done】洛谷P2254 [NOI2005]瑰麗華爾茲
【Todo】洛谷P2569 [SCOI2010]股票交易
【Todo】洛谷P3572 [POI2014]PTA-Little Bird
【Todo】洛谷P3594 [POI2015]WIL-Wilcze doły
決策單調性
一般分兩類。無論是哪一類都需要細心發現決策之間的遞變規律。
一種是用于優化形如\(f_{i}=\min/\max w_{i,j}\)且對于每一個\(i\)和它的最優決策點\(j\)都有單調性的方程。
這樣的方程對題目的性質要求較高(因為\(j\)是獨立的)。
隻需要維護指針,按照單調性不斷尋找最優答案即可。
update:上面提到的這一種好像不在狹義的決策單調性的定義内。。。應該可以叫雙指針優化。
另一種是形如\(f_i=\min/\max_{j=1}^{i-1} g_j+w_{i,j}\),且記\(f_i\)的最優決策點為\(p_i\)(也就是\(f_i\)從\(g_{p_i}+w_{i,p_i}\)處轉移最優)若滿足\(p_i\le p_{i+1}\),則該方程滿足決策單調性。
在詩人小G的題解中蒟蒻用數形結合的思想讨論了一種可能可以快速準确地判斷一個轉移方程是否滿足決策單調性的方法。
因為\(j\)不獨立了,是以我們隻能把有用的決策先存起來。
政策1——二分棧
我們使用決策二分棧(一種單調棧)來維護所有有用的決策,其中棧頂是目前最優決策。
為什麼叫二分棧呢?
我們可以把\(g_j+w_{i,j}\)視為關于\(j\)的函數。因為決策單調,是以對于棧中的任意相鄰兩個決策點,我們都可以通過二分找到一個臨界值\(k\),使得序列中在\(k\)之前的時候,其中一個作為決策轉移到\(f_k\)更優,而\(k\)以後另一個更優。可以借助函數圖像來了解這個過程。
我們需要棧頂為目前的最優解。而如果棧中有不止一個元素,則可能存在一個\(i\),使得到\(i\)之後棧裡面的決策比棧頂優了。這個時候,如何快速判斷并彈掉棧頂呢?
上面提到的這個可二分的性質就派上用場了。對于目前的\(i\),如果目前棧頂下面與棧頂相鄰的決策在\(i\)之前就比棧頂更優了,就要把棧頂彈掉。
這是決策單調性的基本思想,具體的題目實作起來也不一樣。諸如有的題為了擴充功能,還需要把單調棧換成單調隊列,等等。
政策2——分治
然而二分棧有一個局限性,那就是必須能快速計算\(w_{i,j}\)。如果不能\(O(1)\)算的話,在求臨界值\(k\)的時候複雜度會嚴重退化。
既然轉移過程是單調并且離線的,我們考慮分治。假設目前我們求解一段區間\(f_{l,r}\),而所有\(f_{l,r}\)的最優決策點在\([L,R]\)之間。對于\([l,r]\)的中點\(mid\),我們可以暴力掃一遍\(L-mid\),找到它的最優決策點\(k\)。因為決策單調,是以\(f_{l,mid-1}\)的決策落在\([L,k]\)上,而\(f_{mid+1,r}\)的決策落在\([k,R]\)上,變成了兩個規模減半的小問題。
套用分治的複雜度分析,總的時間也是\(n\log n\)的。
兩種政策的代碼難度都不大呢~
廢話,DP當然是重在思維啦!
類型1
【Sol.】洛谷P1973 [NOI2011]Noi嘉年華
【Todo】洛谷P3724 [AH2017/HNOI2017]大佬
類型2
【Done】BZOJ4709 [Jsoi2011]檸檬
【Sol.】洛谷P3515 [POI2011]Lightning Conductor
【Sol.】洛谷P1912 [NOI2009]詩人小G
【Sol.】CF868F Yet Another Minimization Problem(洛谷)(vjudge)
斜率優化
與決策單調性有着說不清的聯系。
仍然是轉移方程形如\(f_i=\min_{j=1}^{i-1}g_j+w_{i,j}\)(\(\max\)同理)
考慮兩個決策\(j_1,j_2\),如果\(j_1\)比\(j_2\)優,那麼\(g_{j_1}+w_{i,j_1}\le g_{j_2}+w_{i,j_2}\)。
這時候根據題目特點把\(w\)展開,如果式子能化成\(\frac{y_{j_1}-y_{j_2}}{x_{j_1}-x_{j_2}}\le k_i\)的形式,那麼我們把每個決策看成點\((x_j,y_j)\)分布在坐标系上,而真正有用的決策點實際上形成了一個凸殼。(由類似線性規劃的尋找最優解的過程可以發現)
上面這段不好了解?下面第一題的Sol對兩種了解斜率優化的方法做了更詳細的分析(最好看第二種,因為第一種有針對性,不通用)(有圖檔喲qwq)
于是我們用資料結構維護凸殼上的所有點,具體實作依題而定。
不管是什麼題,加入決策點的時候要保證斜率遞增/遞減。
如果\(x\)單調,可以用單調棧維護凸殼,轉移時使用目前直線的斜率(線性規劃),在棧内二分最優解。
如果斜率\(k\)單調,那麼用單調隊列維護凸殼,隊首為目前最優決策。轉移之前如果隊首不優就出隊。
引用MashiroSky學長的更完整的套路總結(他的總結戳這裡)
斜率單調暴力移指針
斜率不單調二分找答案
x坐标單調開單調隊列
x坐标不單調開平衡樹|cdq分治
【Sol.】洛谷P2900 [USACO08MAR]土地征用Land Acquisition
【Todo】洛谷P3195 [HNOI2008]玩具裝箱TOY
【Sol.】洛谷P3628 [APIO2010]特别行動隊
【Todo】洛谷P4360 [CEOI2004]鋸木廠選址
【Todo】洛谷P2305 [NOI2014]購票
【Todo】洛谷P1721 [NOI2016]國王飲水記
DP凸優化/WQS二分/帶權二分
WQS的論文(線上)(下載下傳)
這種算法用來解決一類問題——有\(n\)個物品,規定以若幹方式選擇物品有若幹代價,需要在強制選出\(C\)個物品的前提下最大/最小化代價。
一般來說,适用此算法的題目還要有如下一些特點:(設關于\(x\)的函數\(g(x)\)為強制選\(x\)個物品的最值)
- 我們無法直接求出\(g(C)\)的值(廢話,不然幹嘛不直接求);
- 我們可以直接求出\(g\)的最值,以及使\(g(x)\)取到最值的\(x\);
- \(g\)是一個凸函數。
蒟蒻再解釋這是個什麼東東也比不上Creeper_LKF大佬的blog來的清楚明白了。
可是,有沒有大佬和蒟蒻一樣覺得用二分斜率切凸包的這種思路有點不好了解呢?
受超級大佬學哥的啟發,蒟蒻想試着用原函數與導數的互相轉化來了解我們尋找剛好選取\(C\)個物品時的最優解。
這是\(g(x)\)(上方藍色曲線)和\(g'(x)\)(下方紅色曲線)
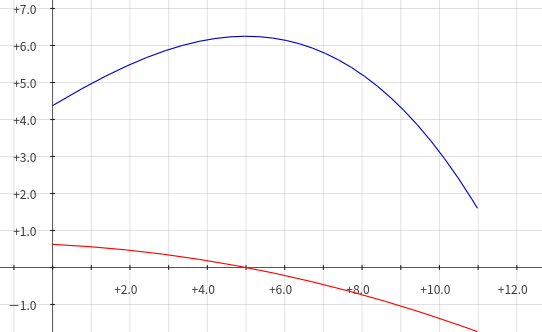
設\(C=7\),現在我們的任務就是求出\(g(7)\)。
顯然,因為\(g(x)\)是凸的,是以\(g'(x)\)是單調遞減的。我們可以求出現在\(g(x)\)的最值,有什麼特點呢?看看\(g'(x)\)與\(x\)軸相交的地方,不就是在這個點處\(g(x)\)取到最值麼?
然而這個交點\(x=5\),不是我們想要的。如果我們能把函數膜改一下,使導函數的交點挪到\(x=7\),那該有多好!
設\(f(x)=g(x)+kx\),\(k\)的現實意義是,我們每多選一個物品,就要多付出\(k\)的代價。
那\(k\)的函數意義又是什麼呢?我們顯然可以發現\(f'(x)=g'(x)+k\),相當于導函數向上平移了\(k\)個機關!而導函數是遞減的,如果我們把它向上平移,那它與\(x\)軸的交點就會向右移了。等于說\(k\)越大交點的\(x\)也越大。這個樣子是可二分的。
于是我們對\(k\)進行二分,\(k\)的值域就是導函數的值域。我們做一遍DP,在原有的轉移基礎上,每多選一個物品還要額外加上\(k\)的代價。最後,我們可以求得\(f(x)\)的極值點,也就是\(f'(x)\)與\(x\)軸的交點。如果這個交點\(x<C\)說明我們仍需繼續調大\(k\),否則就是調小咯。
現在我們試着模拟一下。一開始\(k\)等于\(0\)的時候交點\(x=5<C\),我們就把\(k\)調大一點點。
圖中多了\(f(x)\)(上方綠色曲線)和\(f'(x)\)(下方橙色曲線)
現在的交點\(x=9\),又比\(7\)大了,我們調小\(k\)。
又經過若幹調整,我們終于使得交點落在了\(C\)這個位置。
那麼我們要求出\(g(C)\)了。我們現在求出的是\(f(C)\),隻需要\(g(C)=f(C)-kC\)即可,等于說減掉函數圖像中\(f(x)\)與\(g(x)\)在\(C\)處的高度差。
看上去需要小數二分?不是這樣的。在實際的DP問題中\(x\)肯定都是整數點,那麼\(g(x)\)肯定是一段一段的折線,\(g'(x)\)就是一段一段的水準線,等于說取遍\(g'(x)\)的整數點的值就能取遍\(g'(x)\)的整個值域了。于是在整數内二分即可。
注意上面的\(g(x)\)是上凸的,如果\(g(x)\)下凸那麼\(g'(x)\)遞增,二分的方向還要變一下。
【Sol.】洛谷P2619 [國家集訓隊2]Tree I(不是DP,但有助于了解帶權二分)
【Sol.】洛谷P4072 [SDOI2016]征途
【Done】洛谷P4383 [八省聯考2018]林克卡特樹lct
【Todo】BZOJ5311貞魚
【Todo】洛谷CF739E Gosha is hunting