拓撲排序是否唯一——重建序列115

重建序列

題目：重建序列

    判斷原始的序列 org 是否可以從序列集 seqs 中唯一地重建 。

    重建 是指在序列集 

seqs

 中建構最短的公共超序列，即  

seqs

 中的任意序列都是該最短序列的子序列

案例

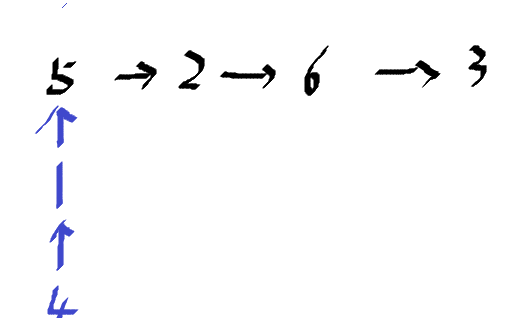
輸入: org = [4,1,5,2,6,3], seqs = [[5,2,6,3],[4,1,5,2]]
輸出: true           

題解

  思路：從序列中尋找拓撲排序，并判斷拓撲排序是否唯一

  拓撲排序唯一：循環中，隊列中每次直郵一個入度為0的點

class Solution {
        public boolean sequenceReconstruction(int[] org, List<List<Integer>> seqs) {
            if (seqs == null || seqs.size() == 0) return false;
            Queue<Integer> queue = new ArrayDeque<>();
            Map<Integer, Set<Integer>> map = new HashMap<>();
            Map<Integer, Integer> degree = new HashMap<>();

            //計算每個點的連接配接點
            for (List<Integer> list : seqs) {
                degree.putIfAbsent(list.get(0), 0);
                for (int i = 1; i < list.size(); i++) {
                    map.putIfAbsent(list.get(i - 1), new HashSet<>());
                    map.get(list.get(i - 1)).add(list.get(i));
                }
            }

            //計算入度
            map.forEach((k, v) -> {
                for (int next : v)
                    degree.merge(next, 1, Integer::sum);
            });

            //入度為0，則入隊列
            if (degree.size() != org.length) return false;
            degree.forEach((k, v) -> {
                if (v == 0) queue.add(k);
            });

            //判斷拓撲排序是否唯一
            int index = 0, res[] = new int[org.length];
            while (!queue.isEmpty()) {
                if (queue.size() > 1) return false;
                int temp = queue.poll();
                res[index++] = temp;
                if (map.get(temp) != null && map.get(temp).size() > 0) {
                    for (int neib : map.get(temp)) {
                        degree.put(neib, degree.get(neib) - 1);
                        if (degree.get(neib) == 0) queue.add(neib);
                    }
                }
            }

            //拓撲排序是否與原序列一緻
            if (index != org.length) return false;
            for (int i = 0; i < org.length; i++)
                if (res[i] != org[i]) return false;
            return true;
        }
    }           

算法小白，歡迎指教