圖文講解,一門教學級邏輯式程式設計語言,NMiniKanren,的運作原理。
本系列前面的文章:
邏輯式程式設計語言極簡實作(使用C#) - 1. 邏輯式程式設計語言介紹
邏輯式程式設計語言極簡實作(使用C#) - 2. 一道邏輯題:誰是兇手
第二天,好為人師的老明繼續開講他的私人課堂。
“今天講NMiniKanren的運作原理。”老明敲了敲白闆,開始塗畫代碼,“我們從一個喜聞樂見的例子開始。”
“這題我會了!”小皮在例子下邊寫下答案:
看到小皮沒把昨天的知識忘光,老明略感欣慰:“不錯。你這個答案是怎麼算出來的呢?”
“呃……就是那個……”小皮忽然卡殼了。這種問題就好比幾何證明題,明明一眼就能看出來的兩條垂直線,真下手證明卻發現還挺不容易。小皮抓了幾把頭發,總算理出一縷思緒:“大概就是找出所有條件可能的組合……然後算一下解……”小皮一邊說,一邊在白闆上寫着:
<code>x == 1</code>
<code>y == x => (x y) == (1 1)</code>
<code>y == "b" => (x y) == (1 "b")</code>
<code>x == 2</code>
<code>y == x => (x y) == (2 2)</code>
<code>y == "b" => (x y) == (2 "b")</code>
“嗯,其實你已經知道怎麼算出答案來了。隻是對于其中的細節還不甚明了。我們接下來要做的事要理清楚這個計算過程,得到一個每一步都可以由計算機明确執行的算法。
“這個算法其實就是你所說這樣,找出所有可能的條件組合。每組條件組合可以求出一個解,也可能自相沖突進而無解。由于NMiniKanren中的條件都是相等條件,是以一組條件組合可以看作一個替換(Substitution)。一個替換能産生一個解,或者無解。
“是以,隻需解決下面兩個問題:
要在什麼資料結構上按照什麼順序周遊替換。
如何從替換中算出一個解,或者判斷其無解。”
首先,我們要從代碼構造出一個資料結構(其實就是一張圖)。這個資料結構能夠按照一定的順序進行周遊,并依次生成替換。
例子中的代碼使用到了<code>Eq</code>、<code>Any</code>和<code>All</code>這三種構造目标的方法。下面分别探讨怎樣從這三種方法構造出我們需要的資料結構來。
“<code>k.Eq(a, b)</code>構造的目标是什麼意思呢?”老明以一個看似平凡的問題開頭。
“簡單,意思就是<code>a</code>要等于<code>b</code>這個條件。”
“孤立地看,是這樣。但是考慮到上下文,更精确地說應該是,在上下文的基礎上追加<code>a</code>等于<code>b</code>這個條件。”
小皮有點不解:“emm……多了‘追加’有什麼不同呢?”
“從文字上看,多了‘追加’後,目标的解釋從一種名詞(一組條件)變成了動詞(追加條件)。這樣一來,目标不僅表達了一組條件,同時也表達了這些條件如何跟上下文結合。就<code>Eq</code>的情況來說,這個結合方式是‘追加’。而<code>Any</code>和<code>All</code>會有其他結合方式。”
“雖然還不是很明白,我想這個要等<code>Any</code>和<code>All</code>的情況一起對比才能清晰起來。我還另外有個問題,上下文指的是什麼?”
“狹義地說,上下文是解釋器運作到這一條代碼時,已執行的代碼生成的替換。
“廣義上看,上下文還應該包含回溯分支等控制資訊,不過目前我們先忽略這些。
“綜合起來,按照對<code>Eq</code>目标的解釋,我們可以用下圖來表示這個目标。”
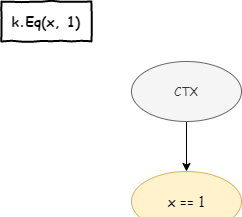
“接着看<code>Any</code>。按照上面的讨論,我們要怎麼解釋<code>Any</code>目标呢?”老明繼續發問。
“解釋目标要說清楚兩個方面:名詞(什麼條件)和動詞(如何與上下文結合)。以一開始的例子中的<code>k.Any(k.Eq(x, 1), k.Eq(x, 2))</code>為例。名詞方面自然就是<code>x</code>等于1和<code>x</code>等于2兩個條件了,不過這兩個條件是‘或’的關系。動詞方面,應該是從上下文分岔出兩個分支,一個分支追加<code>x</code>等于1這個條件,另一個分支追加<code>x</code>等于2這個條件。”
“很好。也就是說,和<code>Eq</code>不同,<code>Any</code>操作和上下文結合後,會生成多個替換。”老明贊許地點點頭,“它把參數的分支都放在一起,就像加法似的。用圖表示的話,就像下面這樣。”
“最後是<code>All</code>……”
“這個我也會了!”小皮打斷老明,“<code>k.All(a, b)</code>名詞上表示條件<code>a</code>且條件<code>b</code>;動詞上表示上下文先追加<code>a</code>,再追加<code>b</code>。”
“你說的太籠統了。<code>a</code>和<code>b</code>可能都有多個分支,這種情況下怎麼做?”老明接着問道。
小皮想了想一開始做的例子,答道:“這種情況要取所有組合,也就是<code>a</code>的分支和<code>b</code>的分支兩兩組合!最後分支數量等于<code>a</code>分支數量乘以<code>b</code>分支數量。”
“很好。如果<code>Any</code>類比加法,那麼<code>All</code>類比的是乘法。下面這圖描述了開頭例子中的<code>All</code>方法的結合過程。
“這是個有向圖,每條邊表示一次追加條件的過程。每條從開始節點(上下文)到結尾的路徑,上面的節點組合起來就是一個替換。周遊所有路徑,我們就周遊了所有替換。而周遊的順序,就是解釋器輸出結果的順序。”
接下來我們還可以來看看<code>Anyi</code>。
普通的<code>Any</code>使用的普通的樹結構周遊順序:
而<code>Anyi</code>以交替的順序周遊分支:
<code>Alli</code>類似采用交替的順序周遊,這裡就不再畫了(主要是不好畫,懶)。
上一篇主要從構造目标的角度出發,介紹了不同方式構造出來的目标。為了實作NMiniKanren的解釋器,我們需要更加深入地了解在解釋器的實作中,Goal是什麼類型。
在前面的讨論中,我們知道,目标的含義是對上下文/一個替換按照某種方式追加一些條件,傳回零個、一個或多個替換——<code>Eq</code>傳回一個;<code>Any</code>和<code>All</code>可能傳回多個;另外前面沒讨論到的<code>Fail</code>會傳回零個。
從這個描述不難看出,最友善表述目标類型的是一個單參數函數,其參數是一個替換,傳回值是替換的枚舉,相當于C#中的<code>Enumerable<替換></code>,也可以說是一個替換的流(Stream)。
<code>Goal(替換)</code>這個函數調用的含義是把Goal包含的條件,追加到替換上,傳回一系列(因為可能有分支,就會變成多個)的替換。
“為什麼不直接用<code>List</code>呢?”小皮又發問了。
“因為很多情況下,分支數量會很多,甚至是無窮多,而我們隻需要挨個取前面幾個結果就夠了。這種情況下使用<code>List</code>會極大降低解釋器效率,甚至造成死循環。”
“略。”
“啥?”小皮瞪了下眼。
“懶得畫,留着思考吧。”
“生成替換後,剩下的就是求解了。
“替換求解的方法很簡單,就是應用一下國小時學過的代入消元法。來,看看這個怎麼解。”老明一邊說一邊寫下例題:
畢竟是國小難度的題目,小皮看了一眼,馬上就有了解法:“<code>x</code>等于1是确定的了,把(3)代入(1)後,<code>y</code>也等于1。把(1)和(3)都代入(2),得到<code>q</code>等于<code>(1 1)</code>。”
“解是求出來了,不過你覺得你這個步驟有通用性嗎?”老明虛着眼說,“計算機能自覺地使用你這個蛇皮順序嗎?”
“呃……”小皮陷入沉思。判斷代入順序的規則似乎還挺麻煩的。或者簡單粗暴按照所有順序都代入一遍?
“其實沒想象中複雜,按順序代入一遍,再反過來代入一遍,就OK了。”
把(1)代入(2)(3):
把(2)代入(3):
在解釋器實作中,條件是一條一條追加上來的。可以每次追加條件的時候,将已有的條件代入新條件,這樣就把這一步化解到生成替換的過程中了。
加入條件(1) <code>y == x</code>:
加入條件(2) <code>q == (x y)</code>:
加入條件(3) <code>x == 1</code>:
把(3)代入(2)(1):
把(2)代入(1):
搞定!
這隻是個簡單的例子。實際情況還可能會出現無解、自由變量以及死循環等情況。這裡就不多贅述了。
“現在能看出NMiniKanren為什麼不支援‘非’運算了嗎?”
小皮認真想了一會,說:“豈止不支援‘非’,‘大于’和‘小于’這些也不行吧。按照代入消元法,NMiniKanren隻支援相等條件。”。
“那如果要支援這些運算應該怎麼做呢?”
“要拓展條件的類型。除了相等條件,還要有不相等條件等。響應的求解算法也要有所變化。”
“沒錯。改動雖然不大,但是代碼看起來會混亂得多。是以以教學為目的的話,就不支援這些了。”
不知不覺時間已到了喜聞樂見的午餐時間,于是老明總結道:“雖然還沒有落地成代碼,但運作原理算是弄清楚了。關鍵點就兩個:
如何從替換中算出一個解,或者判斷其無解。
“第一點,我們從代碼構造了一張圖。該圖的每條路徑對應一個替換,周遊路徑的順序就是周遊替換的順序。同時也明确了目标Goal的類型。
“第二點,我們使用代入消元法,來回兩遍代入解出了所有未知量。”
“接下來可以寫代碼實作NMiniKanren解釋器了吧。”了解了原理後,小皮的十條手指已經饑渴難耐,蚯蚓似的扭動着。
“不着急,下午還要先講一個程式設計小技巧,然後就可以開搞了。”