要了解HashSet,可以按字面上把它分解為兩部分,一方面它表示一個集合(Set),另一方面,它的實作使用了散列法(Hashing)。
<b>集合(</b><b>Set</b><b>)</b>
還記得嗎?在中學裡曾經學過,集合是某些指定對象的全體,集合的三個性質是确定性、互異性和無序性。本文提到的集合正是這個數學概念在計算機中的實作。
這裡比較值得關注的是互異性,在開發中有些時候需要這樣的一個容器。我們經常使用的數組和List<T>本身不能滿足該性質。.NET3.5之前沒有一個類型是直接提供這種支援的,一種方案是采用Hashtable或Dictionary,在存儲資料項的時候,隻使用key,value忽略。.NET3.5(以及以上)提供了HashSet<T>泛型類,終于可以滿足集合的要求了。
集合作為一種資料結構,它的主要操作很簡單,最重要的是<b>添加和移除元素,以及查詢</b>(判斷某個值是否在集合中,枚舉集合中的所有元素)。要實作一個集合類型,首先可以使用簡單的數組,但是數組元素查詢的時間複雜度是O(n);比數組好得多的另一個選擇是二叉搜尋樹,它本身就提供了上述的三個操作,而且速度都很快:O(logn),這種實作一般稱為TreeSet。二叉搜尋樹在操作的時候需要維護元素之間的相對順序,而集合對順序是沒有要求的,是否可以提供更好的時間複雜度呢?
答案就是HashSet,相關的方法是散列法(Hashing),這也是本文的主要内容。關于集合更詳細的讨論(泛型接口ISet<T>,集合之間的操作,如交集、并集等)将在下篇中進行。
<b>散列法</b>
現在再來明确一下目标。我們要實作的Set類要滿足元素的互異性,但不關心元素的順序如何;要支援的操作是<b>添加</b><b>(insert)</b>元素、<b>移除</b><b>(remove)</b>元素、<b>查詢</b><b>(find)</b>(判斷某個值是否在集合中);每種操作的時間複雜度要比O(logn)好。
對于數組來說,如果知道了下标,那麼通路該元素的時間複雜度為O(1),現在看能否利用這一點。考慮一種簡單情況,我們要處理的集合包含若幹小的整數,範圍在0到99之間,并且事先可以确定集合的元素個數不會超過100。此時,可以建立一個長度為100的int數組a,其元素全部初始化為0。對于一個數i,要完成insert(i)操作,隻要執行a[i] = 1;對于remove(i)操作,隻需要a[i] = 0;find(i)操作,可以傳回a[i] == 1(或a[i] > 0)。
三種操作的時間複雜度都是O(1),實作起來也很簡單,看起來不錯。不過它有兩個明顯的問題,如果要儲存的整數不是一個小範圍内的值,而是所有int,那麼<b>數組</b><b>a</b><b>的長度要超過</b><b>40</b><b>億</b>,太不現實;另外,我們要實作的是泛型類,可以容納各種類型的值,如果不是int,而是string,<b>元素本身的值不能用作索引</b>。
上面的兩個問題也是散列法的兩個核心問題。先來看第二個問題:對于非整型的值,如何獲得它對應的數組下标。以string為例,假設它包含的字元都是ASCII字元,對應的int值範圍是0-127。對于“junk”,可以這樣來計算:'j'*128^3 + 'u'*128^2 + 'n'*128^1 + 'k'*128^0,這樣就把一個string值轉換為int值了。不過這種方法會産生巨大的整數,對于“junk”這樣簡單的字元串,産生的值就高達224229227,可以想見,對于複雜一點兒的字元串将是不能接受的。于是又回到了<b>上段中的第一個問題,如何避免使用過于巨大的數組</b>?
如果集合的元素是int類型,雖然int的可能值超過40億,但是在一個特定的問題中,集合的元素個數卻可能很有限。如果元素個數不超過1000,那麼隻需要一個長度為1000的數組就夠了,如果一個值超過了數組下标的上限,可以通過一個函數将該值映射到0-999,這樣的函數稱為散列函數(hash function)。
<b>散列函數</b>
根據上面的分析,對于一個集合S,用來存放元素的數組長度為tableSize,其中的任一進制素e,散列函數h将e映射到0到tableSize之間的一個整數(即數組的一個有效索引),可以記為:
index = h(e, tableSize)
首先針對元素e,根據某種特定的方法計算出它的int值hashCode,然後傳回hashCode % tableSize,這樣傳回值就會落在0到tableSize-1之間。顯然,在散列函數的實作中,最重要的部分就是計算hashCode。你也許已經想到了一個方法,那就是object.GetHashCode(),這裡需要的正是它。該方法是virtual的,這樣它的每個子類都可以提供自己的實作。比如下面的例子:
前面提到過,很多情況下,元素e的取值範圍要比tableSize大得多,這樣就有可能遇到一種情況,對于不同的兩個元素e1和e2,有h(e1, tableSize) == h(e2, tableSize),此時它們被映射到同一個數組索引,這種複雜的情況稱為<b>沖突</b>(<b>collision</b>),在本文後面會讨論如何解決沖突問題。
一般地,一個好的散列函數需要滿足:
容易計算(主要是指散列函數的時間複雜度為常數時間)。
将元素均勻地映射到數組中,減少沖突的可能;
如果元素類型是基元類型,可以使用它們内置的GetHashCode實作,對于自定義類型的實作,将會在下篇中進行讨論。
<b>當沖突發生時</b>
現在我們已經有了散列函數,接下來需要确定當沖突發生時如何化解它。具體來說,如果一個元素e,經過散列函數求值,被散列到的位置已經被另一個元素占據,那麼e應該放在哪裡?
最簡單的方法是,下一個位置。在數組中順序搜尋,直到找到一個空位置。為利用數組的所有空位置,搜尋進行到數組尾部時,可以繞回到第一個位置。這種方法就是<b>線性探測法</b>(linear probing)。
考慮一個例子,數組長度tableSize = 10,要添加的元素是89、18、49、58和9。散列函數的傳回結果為:
hash(89, 10) → 9
hash(18, 10) → 8
hash(49, 10) → 9
hash(58, 10) → 8
hash(9, 10) → 9
索引
insert(89)
insert(18)
insert(49)
insert(58)
insert(9)
49
1
58
2
9
3
4
5
6
7
8
18
89
在添加89和18時,沒有沖突。添加49時,與89沖突,尋找下一個空位置,由于到達數組尾部,繞回,在索引0處存放49;接下來的58和9與此類似。隻要數組足夠大,就可以找到一個空位置。但問題是,“探測”的時間可能會很長,如果隻有一個空位置,那麼要搜遍整個數組才能找到,平均下來要搜尋半個數組,這與我們的每個操作都是常數時間的期望已經相去甚遠了。
再來看find操作,它的探測路徑與insert相同。要找58,從索引8(hash的傳回值)開始,這個位置有一個元素,但不是58;繼續向下看索引9,仍然不是,直到索引1,找到了比對的元素。要找19,從索引9開始,曆經9、0、1、2,最後到了一個空位置3,這說明數組中沒有與之比對的項。
最後是remove操作,不能直接将元素删除(将該位置置空)。從上面分析可以看到,insert和find操作都需要一條探測路徑,如果直接删除,就會打斷這條路徑,進而使find操作失效。如果把89直接删除,那麼49、58和9就都找不到了。
<b>線性探測法的簡單分析</b>
在上面的例子中,向空的數組添加元素時沒有沖突,到後來沖突越來越多,這也是符合我們的直覺的。公共汽車上越擁擠,沖突發生的可能性就越大。在散列法中有一個專門的術語:<b>負載因子(</b><b>load factor</b><b>)</b>。探測散清單的<b>負載因子</b><b>λ</b><b>是表被裝滿的比例</b>,範圍從0(空)到1(滿)。
使用線性探測法時,比較容易産生連續被占據的塊,如果一個元素被散列到這個塊中,就需要連續嘗試以找到下一個可用位置(看上面添加9時)。這種連續聚集的塊稱為<b>初始聚集(</b><b>primary clustering</b><b>)</b>。用線性探測法添加項時,需要嘗試的平均單元數大約是
。
如果λ=0.5,嘗試次數為2.5,還是可以的;如果λ=0.9,那麼嘗試次數就多達50次了(這還是平均數,某些情況比這更糟)。
對于find操作來說,可以分為兩種情況:不成功的和成功的。不成功的情況與insert操作一樣。如果查找成功,需要檢查的平均單元數約為
如果λ=0.5,嘗試次數為1.5;如果λ=0.9,嘗試次數為5.5。
看來λ=0.5是個不錯的選擇,<b>平均</b>探測次數很少,也不會需要大量的空閑位置,而且很容易實作。不過,為了減少探測數,我們需要一種能避免初始聚集的方法,一種選擇就是二次探測法。
<b>二次探測法(</b><b>quadratic probing</b><b>)</b>
線上性探測法中,當發現沖突産生時,我們會從沖突位置開始順序探測下一個可用位置,這正是産生初始聚集的原因。如果散列函數hash的傳回值為h,那麼探測的位置将依次是h + 1,h + 2,...,h + i。探測的位置連續,當然就容易産生聚集了。既然這樣,就不要探測連續的位置了,記為
,現在改為依次探測h + f(1),h + f(2),...,h + f(i)。下面來看二次探測法的使用,還是使用前面的那個例子。
在添加49時,與89沖突,49的最終位置是(9 + 1) % 10 = 0;添加58時,與18沖突,而(8 + 1)位置與89沖突,是以58的最終位置是(8 + 2^2) % 10 = 2;同理,9的位置是3。這裡有個相當重要的地方是,hash值為8的元素和hash值為9的元素探測路徑不同,添加58不會影響到後面添加9,這是比線性探測好的地方。
在編碼之前,我們再來考慮幾個問題,這幾個問題解決後,你會發現二次探測法的實作灰常簡單。這幾個問題是:
使用線性探測法,雖然它可能會比較慢,但它可以保證的是,隻要數組不滿,就可以插入新的值,二次探測法也可以做到這一點嗎?另外,探測路徑中的位置會不會被重複探測到?
線性探測法實作隻需要簡單的計算,二次探測法則需要乘法和模運算,這會不會造成太大的負擔?
如果λ過高怎麼辦?能否動态擴充數組?
對于問題1,如果tableSize為素數,而且λ不超過0.5,就可以解決,即下面的定理:
定理1:如果采用二次探測法并且表(數組)的大小是素數,表至少有一半是空的(即λ <= 0.5),那麼新的元素總能插入,插入過程中沒有一個位置會被探測兩次。
證明:設表的大小為M,M為大于3的奇素數。現在考慮探測序列的前
項(包括初始項),可以證明它們彼此是不同的。這裡使用反證法。假設這些項的某兩個項是
和
,其中
。若這兩項相同且
,那麼
因為M是素數,是以i-j或i+j可以被M整除,因為i和j不同且它們的和小于M,這兩種情況都不可能。可以得出,這兩項是不同的,由于λ>0.5(M為奇數),是以這
項中必然有一項是空位置,這樣元素總能插入,且不會有位置被探測兩次。
對于問題2,線性探測法需要的計算需要一次簡單的加法(加1)、一個确定是否需要繞回表頭的測試,一個很少出現的減法(傳回表頭)。二次探測法需要做一次加法(i – 1到i)、一次乘法(i * i)、一次加法和一次取模,看起來開銷很大。通過下面的定理:
定理2:不需要昂貴的乘法和取模就能實作二次探測法。
簡單說一下證明。探測序列中的相鄰兩項是
和
問題3的出現是因為,要解決問題1,我們需要保證λ不超過0.5,随着元素的增加,需要動态擴充數組,這個過程稱為重散列(rehashing)。擴充為新的數組後,不能簡單的将元素拷貝過去,因為新的tableSize意味着新的散列函數,這裡的做法是重新檢查原有數組的每個元素,将它們添加到新數組中。
現在可以來考慮HashSet的具體實作了,首先來看HashSet的Hash部分,通過散列法實作Set的三種基本操作。HashSet的類圖大緻如下:
這裡通過嵌套類HashEntry來存放集合中的值,前面提到過,不能夠直接删除某個項,而是通過一個IsActive屬性進行辨別。對于主要的三個操作Add(insert)、Remove和Contains(find)來說,它們都需要一個探測序列來找到insert的位置或是查詢是否包含某個值。這個類似的探測過程都放在了FindPos方法中:
1 private int FindPos(T item)
2 {
3 int collisionNum = 0;
4 int pos = (item.IsNull()) ? 0 : Math.Abs(item.GetHashCode() % array.Length);
6 while (array[pos].IsNotNull())
7 {
8 if (item.IsNull())
9 {
10 if (array[pos].Item.IsNull())
11 {
12 break;
13 }
14 }
15 else if (item.Equals(array[pos].Item))
16 {
17 break;
18 }
19
20 pos += 2 * (++collisionNum) - 1;
21 if (pos >= array.Length)
22 {
23 pos -= array.Length;
24 }
25 }
26
27 return pos;
28 }
第4行獲得初始散列值,第20行使用的是定理2中的公式。
有了FindPos方法,三個操作的代碼都變得簡單了:
Add/Remove/Contains方法
到這裡,我們使用二次探測法實作了HashSet的三個基本操作,不過關于GetHashCode方法和ISet接口的實作,這裡還沒有提及,這些留在下一篇中進行讨論。
<b>其它沖突解決方法</b>
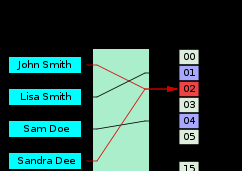
還有一種流行的方法是分離連結法(separate chaining):
如上圖,John Smith和Sandra Dee都散列到了152位置,它們對應的兩個值将形成一個連結清單,也就是它們被放在了同一個桶(bucket)裡,這樣的好處是不會大量的“空桶”,進而節省了空間。了解了二次探測法,這個也比較容易了解。
小結
本文主要讨論了散列法和散列函數的基本概念以及解決散列沖突的兩種方法:線性探測法和二次探測法,并以二次探測法簡單地實作了HashSet的Hash這一部分。在下篇中将會讨論GetHashCode方法在自定義類型中的實作以及給HashSet添加對ISet接口的實作,那樣才算是一個真正的Set。
參考
<a href="http://en.wikipedia.org/wiki/Hash_function">Hash Function</a>
<a href="http://en.wikipedia.org/wiki/Hash_table">Hash Table</a>
本文轉自一個程式員的自省部落格園部落格,原文連結:http://www.cnblogs.com/anderslly/archive/2011/06/13/hashset-part1.html,如需轉載請自行聯系原作者。