通常在現實應用中,我們需要去了解一個變量是如何被一些其他變量所決定的。
回答這樣的問題,需要我們去建立一個模型。一個模型就是一個公式之中,一個因變量(dependent variable)(需要預測的值)會随着一個或多個數值型的自變量(independent variable)(預測變量)而改變的。我們能夠建構的最簡單的模型之一就是線性模型,我們可以假設因變量和自變量間是線性的關系。回歸分方法可用于預測數值型資料以及量化預測結果與其預測變量之間關系的大小及強度。本文将介紹如何将回歸方法應用到你自己的資料中,主要介紹學習内容:
用線性回歸方法來拟合資料方程的基本統計原則和它們如何描述資料元素之間的關系。
如何使用R準備資料進行回歸分析,定義一個線性方程并估計回歸模型。
回歸主要關注确定一個唯一的因變量(dependent variable)(需要預測的值)和一個或多個數值型的自變量(independent variable)(預測變量)之間的關系。我們首先假設因變量和自變量之間的關系遵循一條直線,即線性關系。
你可能還記得數學中是以類似于Y=aX + b的斜截式來定義直線的,其中,y是因變量,x是自變量。在這個公式中,斜率(slope)a表示每增加一個機關的x,直接會上升的高度;變量b表示X=0時y的值,它稱為截距,因為它指定了直線穿過y軸時的位置。
回歸方程使用類似于斜截式的形式對資料建立模型。該機器的工作就是确定a和b的值,進而使指定的直線最适合用來反映所提供的x值和y值之間的關系,這可能不是完美的比對,是以該機器也需要有一些方法來量化誤差範圍,很快我們就會讨論這個問題。
回歸分析通常用來對資料元素之間的複雜關系建立模型,用來估計一種處理方法對結果的影響和推斷未來。一些具體應用案例包括:
根據種群和個體測得的特征,研究他們之間如何不同(差異性),進而用于不同領域的科學研究,如經濟學、社會學、心理學、實體學和生态學;
量化事件及其相應的因果關系,比如可應用于藥物臨床試驗、工程安全檢測、銷售研究等。
給定已知的規則,确定可用來預測未來行為的模型,比如用來預測保險賠償、自然災害的損失、選舉的結果和犯罪率等。
回歸方法也可用于假設檢驗,其中包括資料是否能夠表明原假設更可能是真還是假。回歸模型對關系強度和一緻性的估計提供了資訊用于評估結果是否是由于偶然性造成的。回歸分析是大量方法的一個綜合體,幾乎可以應用于所有的機器學習任務。如果被限制隻能選擇單一的分析方法,那麼回歸方法将是一個不錯的選擇。
本文隻關注最基本的回歸模型,即那些使用直線回歸的模型,這叫做線性回歸(linearregression)。如果隻有一個單一的自變量,那就是所謂的簡單線性回歸(simple linear regression),否則,稱為多元回歸(multiple regression),這兩個模型都假定因變量是連續的。對其他類型的因變量,即使是分類任務,使用回歸方法也是可能的。邏輯回歸(logistic regression)可以用來對二進制分類的結果模組化;泊松分布(Possion regression)可以用來對整型的計數資料模組化。相同的基本原則适用于所有的回歸方法,是以一旦了解了線性情況下的回歸方法,就可以研究其他的回歸方法。
讓我們從基礎開始。記得高中時學過的直線方程嗎?
Y=aX + b
a就是斜率,b就是y軸截距。簡單而言,線性回歸就是一系列技術用于找出拟合一系列資料點的直線。這也可以被認為是從資料之中反推出一個公式。我們會從最基礎的一些規則開始,慢慢增加數學複雜度,增進對這個概念了解的深入程度。但是在此之前,也許你會很好奇這裡的a和b的值分别是多少。接下來,我們通過一個例子,使用軟體R來為我們計算,我們的資料來源于一組真實的關于兒童的身高和年齡,記錄的資料。首先我們先直覺地顯示年齡與身高之間的關系,畫出一張散點圖,以年齡age為橫坐标,身高height為縱坐标,R的代碼如下:
> age=18:29 #年齡從18到29歲
> height=c(76.1,77,78.1,78.2,78.8,79.7,79.9,81.1,81.2,81.8,82.8,83.5)
> plot(age,height,main = "身高與年齡散點圖")
散點圖結果如圖1所示。
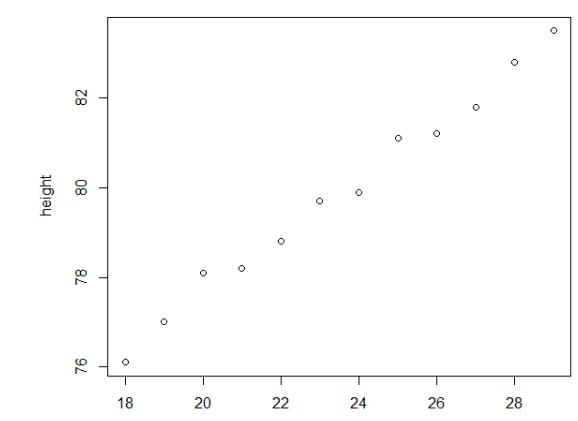
圖1 身高與年齡散點圖
從圖中可以觀察到,年齡與身高基本在一條直線附近,可以認為兩者具有線性關系,接下來建立回歸模型,R代碼如下:
> lm.reg <- lm(height~age) #建立回歸方程
> lm.reg
> abline(lm.reg) #畫出拟合的線性回歸線
産生以下的輸出:
Call:
lm(formula = height ~ age)
cients:
(Intercept) age
64.928 0.635
圖2 身高與年齡拟合直線
我們可以看到兩個數值,“截距”和“斜率”。無論我們用什麼軟體來做線性回歸(本文中的例子統一采用R語言),它都會用某種形式來報告這兩個數值。截距就是我們的公式中的b,斜率就是Y和自變量之間的傾斜程度。
總結起來,我們有一個資料集(觀測值)和一個模型(我們猜測可以拟合資料的一個公式),我們還要去找出模型的參數(我們的最佳拟合模型中的參數a和b),這樣,模型就可以“最佳”拟合資料了。我們希望用我們的資料來找出一個公式的參數,這樣,這個公式也能夠“最佳”拟合資料了。
1. 用模型來做預測
一旦你目測出最佳拟合直線并且讀出a和b,也許你大概會說大意是這樣的話:“這些資料遵循一個形式為Y = aX + b 的線性方程,其中a(斜率)= 某個數,b(y軸截距)= 另外某個數”。你也許記得,這個等式并非是确切的表述,因為很有可能你的資料并不是所有的都在一條完美的直線上,是以資料點之間可能會有不同程度的誤差。你的目測是主觀地嘗試把一些直覺上的總的誤差給降到最低。你做的事情就是直覺上的“線性回歸”。你按照“我看起來很順眼”的算法來估計a和b。我們會以這個直覺的行為為開端,并迅速帶入一些重量級的機械,使得我們能夠解決一些相當複雜的問題。
在這個節點,你的實驗室練習也許會要求你為不在你的觀測值集合以内的,某個給定數值的X,給出Y的估值。然後你就會用上面的等式,比如說a是2.1,b是0.3的等式Y = 2.1 X + 0.3作為你的模型,你把X輸入進去,就會得到一個Y。這時候你就是在用你的模型去預測一個值,換句話說,你正在陳述這樣的事實:我在實驗之中并沒有用這個X值,并且我的資料裡也沒有它,但是我想要知道這個X值是怎樣投射到Y軸上的。你也許會想要能夠說出:“我的誤差會是某個數,是以我相信實際上的值會在[Y-誤差,Y+誤差]之間”。在這樣的情況下,我們把變量X叫做“預測變量”,而Y的值是基于X的一個值來預測的,是以變量Y是“反應”。
2. 一個概念:總誤差
我們想要創造一個有關誤差,或者說我們的直線所給出的Y值與我們資料集中的真實Y值之間的差異的簡單公式。除非我們的直線正好穿過一個特定的點,否則,這個誤差是非零的。它可能是正值,也可能是負值。我們可以取這個誤差的平方(或者我們也可以取它的絕對值),然後我們把每個點的誤差項相加起來,然後得到直線和這個資料集的總誤差。在同一個實驗的不同的樣例集合中,我們會得到一個不同的資料集,很有可能一條不同的直線,并且幾乎可以肯定一個不同的總誤差。我們所用的誤差的平方值是一個非常常用的總誤差形式,它就是“方差”。它用同樣的方式來處理正值的誤差和負值的誤差,是以方差總是正值的。從現在開始我們會使用“方差”作為我們誤差的代表。總的來說,回歸是我們所使用的任意的資料,最小化方差,來估測模型系數的手段。統計軟體用多變量微積分這些專業技術來最小化誤差,并且給我們提供系數的估測值。對于回歸方程回歸系數的檢驗,檢驗一般用方差分析或t檢驗,兩者的檢驗結果是等價的。方差分析主要是針對整個模型的,而t檢驗是關于回歸系數的。
對于上例中的回歸方程,我們對模型進行檢驗,方差分析的R代碼如下:
> anova(lm.reg) #模型方差分析
Analysis of Variance Table
Response: height
Df Sum Sq Mean Sq F value Pr(>F)
age 1 57.655 57.655 879.99 4.428e-11 ***
Residuals 10 0.655 0.066
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
由于P<0.05,于是在α=0.05水準下,本例的回歸系數有統計學意義,身高和年齡存在直線回歸關系。
同理,對于上例中的回歸方程,我們對模型進行回歸系數的t檢驗,t檢驗的R代碼如下:
> summary(lm.reg) #回歸系數的t檢驗
Residuals:
Min 1Q Median 3Q Max
-0.27238 -0.24248 -0.02762 0.16014 0.47238
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 64.9283 0.5084 127.71 < 2e-16 ***
age 0.6350 0.0214 29.66 4.43e-11 ***
Residual standard error: 0.256 on 10 degrees of freedom
Multiple R-squared: 0.9888,Adjusted R-squared: 0.9876
F-statistic: 880 on 1 and 10 DF, p-value: 4.428e-11
同方差分析,由于P<0.05,于是在α=0.05水準下,本例的回歸系數有統計學意義,身高和年齡存在回歸關系。
很自然地,如果Y依賴于多于一個變量的時候,會發生什麼。這時候,數學上的普遍性的力量就顯現了。這個簡單的原理在多元的情況下同樣适用。不僅僅是兩個或者三個,還有更多更大的數值。如果我們想要建構現實資料的模型的話,二十個,三十個,甚至百來個自變量都毫無問題。但現在我們就看看Y,作為一個含有多個自變量的函數,例如含有來個自變量X1和X2的形式:
Y = a0 + a1X1 + a2X2
這裡的a0 就是截距項,a1,a2 就是自變量X1 ,X2 的系數。 為了看看具有多個潛在的自變量的真實資料集,我們會在下一步使用具體的資料——醫療費用的資料。
多元線性回歸優缺點
優點
缺點
迄今為止,它是數值型資料模組化最常用的方法
對資料做出了很強的假設
可适用于幾乎所有的資料
該模型的形式必須由使用者事先指定
提供了特征(變量)與結果之間關系的強度和大小的估計
不能很好地處理缺失資料
隻能處理數值特征,是以分類資料需要額外的處理
需要一些統計知識來了解模型
醫療費用很難估計,因為花費最高的情況是罕見的而且似乎是随機的。但是有些情況對于部分特定的群體還是比較普遍存在的。例如,吸煙者比不吸煙者得肺癌的可能性更大,肥胖的人更有可能得心髒病。此分析的目的是利用病人的資料,來預測這部分群體的平均醫療費用。這些估計可以用來建立一個精算表,根據預期的治療費用來設定年度保費價格是高一點還是低一點。我們想要去探索這些資料,嘗試從中獲得一些對于建立線性回歸模型有用處的見解。
我們會依據以下步驟完成,将來,我們還會對其他資料集座同樣的事情。
1) 收集/觀察資料;
2) 探索和準備資料;
3) 基于資料訓練模型;
4) 評估模型的性能;
5) 提高模型的性能。
第1步——收集/觀察資料
為了便于分析,我們使用一個模拟資料集,該資料集包含了美國病人的醫療費用。而本文建立的這些資料使用了來自美國人口普查局(U.S. Census Bureau)的人口統計資料,是以可以大緻反映現實世界的情況。
注:如果你想一起學習這個例子,那麼你需要從Packt出版社的網站(https://github.com/stedy/Machine-Learning-with-R-datasets/find/master)下載下傳insurance.csv檔案,并将該檔案儲存到R的工作檔案夾中。
該檔案(insurance.csv)包含1338個案例,即目前已經登記過的保險計劃受益者以及表示病人特點和曆年計劃計入的總的醫療費用的特征。這些特征是:
age: 這是一個整數,表示主要受益者的年齡(不包括超過64歲的人,因為他們一般由政府支付)。
sex: 這是保單持有人的性别,要麼是male,要麼是female。
bmi: 這是身體品質指數(Body Mass Index,BMI),它提供了一個判斷人的體重相對于身高是過重還是偏輕的方法,BMI指數等于體重(公斤)除以身高(米)的平方。一個理想的BMI指數在18.5~24.9的範圍内。
children: 這是一個整數,表示保險計劃中所包括的孩子/受撫養者的數量。
smoker: 根據被保險人是否吸煙判斷yes或者no。
region: 根據受益人在美國的居住地,分為4個地理區域:northeast、southeast、southwest和northwest。
如何将這些變量與已結算的醫療費用聯系在一起是非常重要的。例如,我們可能認為老年人和吸煙者在大額醫療費用上是有較高的風險。與許多其他的方法不同,在回歸分析中,特征之間的關系通常由使用者指定而不是自動檢測出來。
第2步——探索和準備資料
在R中,我們将使用read.csv()函數來加載用于分析的資料。我們可以使用stringAsFactors = TRUE,因為将名義變量轉換成因子變量是恰當的:
> insurance <- read.csv("insurance.csv",stringsAsFactors = TRUE)
函數str()确認該資料轉換了我們之前所期望的形式:
> str(insurance)
'data.frame':1338 obs. of 7 variables:
$ age : int 19 18 28 33 32 31 46 37 37 60 ...
$ sex : Factor w/ 2 levels "female","male": 1 2 2 2 2 1 1 1 2 1 ...
$ bmi : num 27.9 33.8 33 22.7 28.9 ...
$ children: int 0 1 3 0 0 0 1 3 2 0 ...
$ smoker : Factor w/ 2 levels "no","yes": 2 1 1 1 1 1 1 1 1 1 ...
$ region : Factor w/ 4 levels "northeast","northwest",..: 4 3 3 2 2 3 3 2 1 2 ...
$ charges : num 16885 1726 4449 21984 3867 ...
既然因變量是changes,那麼讓我們一起來看一下它是如何分布的:
> summary(insurance$charges)
Min. 1st Qu. Median Mean 3rd Qu. Max.
1122 4740 9382 13270 16640 63770
因為平均數遠大于中位數,表明保險費用的分布是右偏的,我們可以用直方圖證明這一點。
> hist(insurance$charges)
圖3 charges直方圖
在我們的資料中,絕大多數的個人每年的費用都在0~15000美元,盡管分布的尾部經過直方圖的峰部後延伸得很遠。即将面臨的另一個問題就是回歸模型需要每一個特征都是數值型的,而在我們的資料框中,我們有3個因子類型的特征。很快,我們會看到R中的線性回歸函數如何處理我們的變量。
1.探索特征之間的關系——相關系數矩陣
在使用回歸模型拟合資料之前,有必要确定自變量與因變量之間以及自變量之間是如何相關的。相關系數矩陣(correlation matrix)提供了這些關系的快速概覽。給定一組變量,它可以為每一對變量之間的關系提供一個相關系數。
為insurance資料框中的4個數值型變量建立一個相關系數矩陣,可以使用cor()指令:
> cor(insurance[c("age","bmi","children","charges")])
age bmi children charges
age 1.0000000 0.1092719 0.04246900 0.29900819
bmi 0.1092719 1.0000000 0.01275890 0.19834097
children 0.0424690 0.0127589 1.00000000 0.06799823
charges 0.2990082 0.1983410 0.06799823 1.00000000
該矩陣中中的相關系數不是強相關的,但還是存在一些顯著的關聯。例如,age和bmi顯示出中度相關,這意味着随着年齡(age)的增長,身體品質指數(bmi)也會增加。此外,age和charges,bmi和charges,以及children和charges也都呈現處中度相關。當我們建立最終的回歸模型時,我們會盡量更加清晰地梳理出這些關系。
2.可視化特征之間的關系——散點圖矩陣
或許通過使用散點圖,可視化特征之間的關系更有幫助。雖然我們可以為每個可能的關系建立一個散點圖,但對于大量的特征,這樣做可能會變得比較繁瑣。
另一種方法就是建立一個散點圖矩陣(scatterplot matrix),就是簡單地将一個散點圖集合排列在網格中,裡邊包含着互相緊鄰在一起的多種因素的圖表。它顯示了每個因素互相之間的關系。斜對角線上的圖并不符合這個形式。為何不符合呢?在這個語境下,這意味着找到某個事物和自身的關系,而我們正在嘗試确定某些變量對于另一個變量的影響。預設的R中提供了函數pairs(),該函數産生散點圖矩陣提供了基本的功能。對醫療費用資料之中的四個變量的散點圖矩陣如下圖所示。R代碼如下:
pairs(insurance[c("age","bmi","children","charges")])
圖4 散點圖矩陣
與相關系數矩陣一樣,每個行與列的交叉點所在的散點圖表示其所在的行與列的兩個變量的相關關系。由于對角線上方和下方的x軸和y軸是交換的,是以對角線上方的圖和下方的圖是互為轉置的。
你注意到這些散點圖中的一些圖案了嗎?盡管有一些看上去像是随機密布的點,但還是有一些似乎呈現了某種趨勢。age和charges之間的關系呈現出幾條相對的直線,而bmi和charges的散點圖構成了兩個不同的群體。
如果我們對散點圖添加更多的資訊,那麼它就會更加有用。一個改進後的散點圖矩陣可以用psych包中的pairs.panels()函數來建立。R中如果你還沒有安裝這個包,那麼可以輸入install.packages("psych")指令将其安裝到你的系統中,并使用library(psych)指令加載它。R代碼及散點圖矩陣如下:
pairs.panels(insurance[c("age","bmi","children","charges")])
圖5 散點圖矩陣
在對角線的上方,散點圖被相關系數矩陣所取代。在對角線上,直方圖描繪了每個特征的數值分布。最後,對角線下方的散點圖帶有額外的可視化資訊。
每個散點圖中呈橢圓形的對象稱為相關橢圓(correlation ellipse),它提供了一種變量之間是如何密切相關的可視化資訊。位于橢圓中心的點表示x軸變量的均值和y軸變量的均值所确定的點。兩個變量的相關性由橢圓的形狀所表示,橢圓越被拉伸,其相關性越強。一個幾乎類似于圓的完美的橢圓形,如bmi和children,表示一種非常弱的相關性。
散點圖中繪制的曲線稱為局部回歸平滑(loess smooth),它表示x軸和y軸變量之間的一般關系。最好通過例子來了解。散點圖中age和childr的曲線是一個倒置的U,峰值在中年附近,這意味着案例中年齡最大的人和年齡最小的人比年齡大約在中年附近的人擁有的孩子更少。因為這種趨勢是非線性的,是以這一發現已經不能單獨從相關性推斷出來。另一方面,對于age和bmi,局部回歸光滑是一條傾斜的逐漸上升的線,這表明BMI會随着年齡(age)的增長而增加,從相關系數矩陣中我們也可推斷出該結論。
第3步——基于資料訓練模型
用R對資料拟合一個線性回歸模型時,可以使用lm()函數。該函數包含在stats添加包中,當安裝R時,該包已經被預設安裝并在R啟動時自動加載好。使用R拟合稱為ins_model的線性回歸模型,該模型将6個自變量與總的醫療費用聯系在一起。代碼如下:
ins_model <- lm(charges~age+children+bmi+sex+smoker+region,data=insurance)
建立模型後,隻需輸入該模型對象的名稱,就可以看到估計的a系數:
> ins_model
lm(formula = charges ~ ., data = insurance)
(Intercept) age sexmale
-11938.5 256.9 -131.3
bmi children smokeryes
339.2 475.5 23848.5
regionnorthwest regionsoutheast regionsouthwest
-353.0 -1035.0 -960.1
你可能注意到,在我們的模型公式中,我們僅指定了6個變量,但是輸出時,除了截距項外,卻輸出了8個系數。之是以發生這種情況,是因為lm()函數自動将一種稱為虛拟編碼(dummy coding)的技術應用于模型所包含的每一個因子類型的變量中。當添加一個虛拟編碼的變量到回歸模型中時,一個類别總是被排除在外作為參照類别。然後,估計的系數就是相對于參照類别解釋的。在我們的模型中,R自動保留sexfemale、smokerno和regionnortheast變量,使東北地區的女性非吸煙者作為參照組。是以,相對于女性來說,男性每年的醫療費用要少$131.30;吸煙者平均多花費$23848.50,遠超過非吸煙者。此外,模型中另外3個地區的系數是負的,這意味着東北地區傾向于具有最高的平均醫療費用。
線性回歸模型的結果是合乎邏輯的。高齡、吸煙和肥胖往往與其他健康問題聯系在一起,而額外的家庭成員或者受撫養者可能會導緻就診次數增加和預防保健(比如接種疫苗、每年體檢)費用的增加。然而,我們目前并不知道該模型對資料的拟合有多好?我們将在下一部分回答這個問題。
第4步——評估模型的性能
通過在R指令行輸入ins_model,可以獲得參數的估計值,它們告訴我們關于自變量是如何與因變量相關聯的。但是它們根本沒有告訴我們用該模型來拟合資料有多好。為了評估模型的性能,可以使用summary()指令來分析所存儲的回歸模型:
> summary(ins_model)
-11304.9 -2848.1 -982.1 1393.9 29992.8
Estimate Std. Error t value Pr(>|t|)
(Intercept) -11938.5 987.8 -12.086 < 2e-16 ***
age 256.9 11.9 21.587 < 2e-16 ***
sexmale -131.3 332.9 -0.394 0.693348
bmi 339.2 28.6 11.860 < 2e-16 ***
children 475.5 137.8 3.451 0.000577 ***
smokeryes 23848.5 413.1 57.723 < 2e-16 ***
regionnorthwest -353.0 476.3 -0.741 0.458769
regionsoutheast -1035.0 478.7 -2.162 0.030782 *
regionsouthwest -960.0 477.9 -2.009 0.044765 *
Residual standard error: 6062 on 1329 degrees of freedom
Multiple R-squared: 0.7509,Adjusted R-squared: 0.7494
F-statistic: 500.8 on 8 and 1329 DF, p-value: < 2.2e-16
開始時,summary()的輸出可能看起來令人費解,但基本原理是很容易掌握的。與上述輸出中用标簽編号所表示的一樣,該輸出為評估模型的性能提供了3個關鍵的方面:
1) Residuals(殘差)部分提供了預測誤差的主要統計量;
2) 星号(例如,***)表示模型中每個特征的預測能力;
3) 多元R方值(也稱為判定系數)提供度量模型性能的方式,即從整體上,模型能多大程度解釋因變量的值。
給定前面3個性能名額,我們的模型表現得相當好。對于現實世界資料的回歸模型,R方值相當低的情況并不少見,是以0.75的R方值實際上是相當不錯的。考慮到醫療費用的性質,其中有些誤差的大小是需要關注的,但并不令人吃驚。如下節所述,我們會以略微不同的方式來指定模型,進而提高模型的性能。
第5步——提高模型的性能
正如前面所提到的,回歸模型通常會讓使用者來選擇特征和設定模型。是以,如果我們有關于一個特征是如何與結果相關的學科知識,我們就可以使用該資訊來對模型進行設定,并可能提高模型的性能。
1. 模型的設定——添加非線性關系
線上性回歸中,自變量和因變量之間的關系被假定為是線性的,然而這不一定是正确的。例如,對于所有的年齡值來講,年齡對醫療費用的影響可能不是恒定的;對于最老的人群,治療可能會過于昂貴。
2. 轉換——将一個數值型變量轉換為一個二進制名額
假設我們有一種預感,一個特征的影響不是累積的,而是當特征的取值達到一個給定的門檻值後才産生影響。例如,對于在正常體重範圍内的個人來說,BMI對醫療費用的影響可能為0,但是對于肥胖者(即BMI不低于30)來說,它可能與較高的費用密切相關。我們可以通過建立一個二進制名額變量來建立這種關系,即如果BMI大于等于30,那麼設定為1,否則設定為0。
注:如果你在決定是否要包含一個變量時遇到困難,一種常見的做法就是包含它并檢驗其顯著性水準。然後,如果該變量在統計上不顯著,那麼就有證據支援在将來排除該變量。
3. 模型的設定——加入互相作用的影響
到目前為止,我們隻考慮了每個特征對結果的單獨影響(貢獻)。如果某些特征對因變量有綜合影響,那麼該怎麼辦呢?例如,吸煙和肥胖可能分别都有有害的影響,但是假設它們的共同影響可能會比它們每一個單獨影響之和更糟糕是合理的。
當兩個特征存在共同的影響時,這稱為互相作用(interaction)。如果懷疑兩個變量互相作用,那麼可以通過在模型中添加它們的互相作用來檢驗這一假設,可以使用R中的公式文法來指定互相作用的影響。為了展現肥胖名額(bmi30)和吸煙名額(smoker)的互相作用,可以這樣的形式寫一個公式:charge~bmi30*smoker。
4. 全部放在一起——一個改進的回歸模型
基于醫療費用如何與患者特點聯系在一起的一點學科知識,我們采用一個我們認為更加精确的專用的回歸公式。下面就總結一下我們的改進:
增加一個非線性年齡項
為肥胖建立一個名額
指定肥胖與吸煙之間的互相作用
我們将像之前一樣使用lm()函數來訓練模型,但是這一次,我們将添加新構造的變量和互相作用項:
> ins_model2 <-lm(charges~age+age2+children+bmi+sex+bmi30*smoker+region,data=insurance)
接下來,我們概述結果:
> summary(ins_model2)
lm(formula = charges ~ age + age2 + children + bmi + sex + bmi30 *
smoker + region, data = insurance)
-17296.4 -1656.0 -1263.3 -722.1 24160.2
Estimate Std. Error t value Pr(>|t|)
(Intercept) 134.2509 1362.7511 0.099 0.921539
age -32.6851 59.8242 -0.546 0.584915
age2 3.7316 0.7463 5.000 6.50e-07 ***
children 678.5612 105.8831 6.409 2.04e-10 ***
bmi 120.0196 34.2660 3.503 0.000476 ***
sexmale -496.8245 244.3659 -2.033 0.042240 *
bmi30 -1000.1403 422.8402 -2.365 0.018159 *
smokeryes 13404.6866 439.9491 30.469 < 2e-16 ***
regionnorthwest -279.2038 349.2746 -0.799 0.424212
regionsoutheast -828.5467 351.6352 -2.356 0.018604 *
regionsouthwest -1222.6437 350.5285 -3.488 0.000503 ***
bmi30:smokeryes 19810.7533 604.6567 32.764 < 2e-16 ***
Residual standard error: 4445 on 1326 degrees of freedom
Multiple R-squared: 0.8664,Adjusted R-squared: 0.8653
F-statistic: 781.7 on 11 and 1326 DF, p-value: < 2.2e-16
分析該模型的拟合統計量有助于确定我們的改變是否提高了回歸模型的性能。相對于我們的第一個模型,R方值從0.75提高到約0.87,我們的模型現在能解釋醫療費用變化的87%。此外,我們關于模型函數形式的理論似乎得到了驗證,高階項age2在在統計上是顯著的,肥胖名額bmi30也是顯著的。肥胖和吸煙之間的互相作用表明了一個巨大的影響,除了單獨吸煙增加的超過$13404的費用外,肥胖的吸煙者每年要另外花費$19810,這可能表明吸煙會加劇(惡化)與肥胖有關的疾病。
原文釋出時間為:2017-06-11
本文作者:慕生鵬
本文來自雲栖社群合作夥伴“資料派THU”,了解相關資訊可以關注“資料派THU”微信公衆号