本章中,我们将首先学习如何用r语言挖掘频繁模式、关联规则及相关规则。然后,我们将使用基准数据评估所有这些方法以便确定频繁模式和规则的兴趣度。本章内容主要涵盖以下几个主题:
关联规则和关联模式概述
购物篮分析
混合关联规则挖掘
序列数据挖掘
高性能算法
关联规则挖掘算法可以从多种数据类型中发现频繁项集,包括数值数据和分类数据。根据不同的适用环境,关联规则挖掘算法会略有差异,但大多算法都基于同一个基础算法,即apriori算法。另一个基础算法称为fp-growth算法,与apriori算法类似。大多数的与模式相关的挖掘算法都是来自这些基础算法。
将找到的频繁模式作为一个输入,许多算法用来发现关联规则或相关规则。每个算法仅仅是基础算法一个变体。
随着不同领域中的数据集大小和数据类型的增长,提出了一些新的算法,如多阶段算法、多重散列算法及有限扫描算法。
数据挖掘的一个最受欢迎的任务就是发现源数据集之间的关系,它从不同的数据源(如购物篮数据、图数据或流数据)中发现频繁模式。
为了充分理解关联规则分析的目的,本章中所有算法均用r语言编写,这些代码使用算法的标准r添加包(如arules添加包)进行说明。
在众多的领域应用中,频繁模式挖掘经常用于解决各种问题,比如大型购物中心的市场调查可以通过分析购物交易数据来完成。
频繁模式是经常出现在数据集中的模式。频繁模式挖掘的数据类型可以是项集、子序列或子结构。因此,频繁模式也可称为:
频繁项集
频繁子序列
频繁子结构
接下来的章节将详细介绍这3种频繁模式。
当从给定的数据集中发现重复出现的有意义的规则或关系时,这些新发现频繁模式将作为一个重要的平台。
为了提高挖掘数据集的效率,提出了不同的模式。本章列举了以下几种模式,后面将给出它们详细的定义。
封闭模式
最大模式
近似模式
紧凑模式
判别式频繁模式
频繁项集的概念来源于真实的购物篮分析。在诸如亚马逊等商店中,存在很多的订单或交易数据。当客户进行交易时,亚马逊的购物车中就会包含一些项。商店店主可以通过分析这些大量的购物事务数据,发现顾客经常购买的商品组合。据此,可以简单地定义零个或多个项的组合为项集。
我们把一项交易称为一个购物篮,任何购物篮都有组元素。将变量s设置为支持阈值,我们可以将它和一组元素在所有的购物篮中出现的次数做比较,如果这组元素在所有购物篮中出现的次数不低于s,我们就将这组元素称为一个频繁项集。
若一个项集包含有k个项,则该项集称为k项集,其中k是非零整数。项集x的支持计数记为support_count(x),表示给定数据集中包含项集x的计数。
给定一个预先定义的最小支持度阈值s,如果support_count(x)≥s,则称项集x为频繁项集。最小支持度阈值s是一个可以自定义的参数,可以根据领域专家或经验进行调整。
频繁项集也经常应用于许多领域,如下表所示。
如果某个项集是频繁的,那么该项集的任何一个子集也一定是频繁的。这称为apriori原理,它是apriori算法的基础。apriori原理的直接应用就是用来对大量的频繁项集进行剪枝。
影响频繁项集数目的一个重要因素是最小支持计数:最小支持计数越小,频繁项集的数目也越多。
为了优化频繁项集生成算法,人们提出一些其他概念:
闭项集:给定数据集s,如果y∈s, x y,则support_count (x) ≠ support_count (y),那么x称作闭项集。换言之,如果x是频繁的,则x是频繁闭项集。
最大频繁项集:如果y∈s, x y,x是最大频繁项集,则y是非频繁的。换言之,y没有频繁超集。
约束频繁项集:若频繁项集x满足用户指定的约束,则x称为约束频繁项集。
近似频繁项集:若项集x只给出待挖掘数据近似的支持计数,则称为近似频繁项集。
top-k频繁项集:给定数据集s和用户指定的整数k,若x是前k个频繁项集,则x称为top-k频繁项集。
下面给出一个事务数据集的例子。所有项集仅包含集合d = {ik |{k∈[1,7]}中的项。假定最小支持度计数为3。
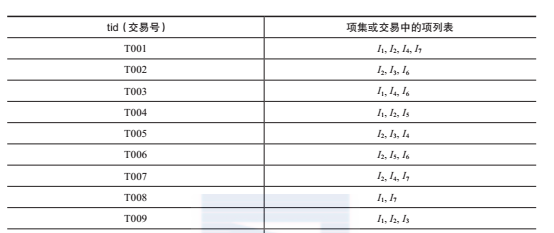
那么,可以得到频繁项集l1 = {ik | k∈{1, 2, 4, 6, 7}}和l2 = {{i1, i2},{i1, i4},{i2, i4}}。
频繁子序列是元素的一个有序列表,其中每个元素包含至少一个事件。一个例子是某网站页面访问序列,具体而言,它是某个用户访问不同网页的顺序。下面给出了频繁子序列的两个例子。
消费者数据:某些客户在购物商城连续的购物记录可作为序列,购买的每个商品作为事件项,用户一次购买的所有项作为元素或事务。
网页使用数据:访问www历史记录的用户可作为一个序列,每个ui/页面作为一个事件或项目,元素或事务定义为用户通过一次鼠标的单击访问的页面。
序列中包含的项数定义为序列的长度。长度为k的序列定义为k序列。序列的大小定义为序列中项集的数目。当满足1≤j1≤j2≤…≤jr-1≤jr≤v,且a1bj1, a2bj2, …, arbjr,则称序列s1=为序列s2=的子序列或s2为s1的超序列。
在某些领域中,研究任务可借助图论来进行建模。因此,需要挖掘其中常见的子图(子树或子格)。例如:
网络挖掘:网页视为图的顶点,网页之间的链接视为图的边,用户的页面访问记录用来构造图。
网络计算:网络上具有计算能力的任何设备作为顶点,这些设备之间的相互连接作为边。由这些设备和设备之间的相互连接组成的整个网络视为图。
语义网络:xml元素视为顶点,元素之间的父/子关系视为边。所有的xml文件可视为图。
图g表示为:g = (v, e),其中v表示顶点的集合,e表示边的集合。当v′v且e′e,图g′= (v′, e′)称为g=(v, e)的子图。下图给出一个子图的例子。图中,左边是原始图及其包含的顶点和边,右边是删除多条边(或删除多个顶点)后的子图。
基于已发现的频繁模式,可以挖掘关联规则。根据关系的兴趣度的不同侧重点,可以进一步研究以下两种类型的关系:关联规则和相关规则。
关联分析可以从海量数据集中发现有意义的关系,这种关系可以表示成关联规则的形式或频繁项集的形式。具体的关联分析算法将在后面一个章节中给出。
关联规则挖掘旨在发现给定数据集(事务数据集或其他序列-模式-类型数据集)中的结果规则集合。给定预先定义的最小支持度计数s和置信度c,给定已发现的规则x→y support_count (x→y)≥s且confidence (x→y)≥c。
当x∩y=(x、y不相交),则x→y是关联规则。规则的兴趣度通过支持度(support)和置信度(confidence)来测量。支持度表示数据集中规则出现的频率,而置信度测量在x出现的前提下,y出现的可能性。
对于关联规则,衡量规则可用性的核心度量是规则的支持度和置信度。两者之间的关系是:
support_count(x)是数据集中包含x的项集数。
通常,在support_count(x)中,支持度和置信度的值表示为0~100的百分数。
给定最小支持度阈值s和最小置信度阈值c。如果support_count (x→y) > s且confidence (x→y)≥c,则关联规则x→y称为强规则。
对于关联规则含义的解释应当慎重,尤其是当不能确定地判断规则是否意味着因果关系时。它只说明规则的前件和后件同时发生。以下是可能遇到不同种类的规则:
布尔关联规则:若规则包含项出现的关联关系,则称为布尔关联规则。
单维关联规则:若规则最多包含一个维度,则为单维关联规则。
多维关联规则:若规则至少涉及两个维度,则为多维关联规则。
相关关联规则:若关系或规则是通过统计相关进行测量的,满足给定的相关
性规则,则称为相关关联规则。
定量关联规则:若规则中至少一个项或属性是定量的,则称为定量关联规则。
在某些情况下,仅仅凭借支持度和置信度不足以过滤掉那些无意义的关联规则。此时,需要利用支持计数、置信度和相关性对关联规则进行筛选。
计算关联规则的相关性有很多方法,如卡方分析、全置信度分析、余弦分析等。对于k项集x={i1, i2 …, ik},x的全置信度值定义为: