1、数字
123 1.23e2
-0.125 1.25E-1 2、逻辑
布尔型,常量值只有
TRUE
和
FALSE
。
**注意:**R 语言区分大小写,true 或 True 不能代表 TRUE。
3、字符串
在 R 语言中,字符串既可以用单引号包含,也可以用双引号包含
| 字符串函数 | 说明 |
| toupper(“xxx”) | 转换为大写 |
| tolower(“xxx”) | 转换为小写 |
| ncahr(“xxx”, type=“bytes”) | 统计字节长度 |
| ncahr(“xxx”, type=“char”) | 统计字符长度 |
| substr(“123456”, 1, 5) | 截取字符串,从1到5 |
| substring(“1234567890”, 5) | 截取字符串,从5到结束 |
| as.numeric(“12”) | 将字符串转换为数字 |
| as.character(12.34) | 将数字转换为字符串 |
| strsplit(“2019;10;1;”, “;”) | 分隔符拆分字符串 |
| gsub(“/”, “-”, “2019/10/1”) | 替换字符串2019-10-1 |
在 Windows 计算机上实现,使用的是 GBK 编码标准,所以一个中文字符是两个字节,如果在 UTF-8 编码的计算机上运行,单个中文字符的字节长度应该是 3。
4、向量
向量从数据结构上看就是一个线性表,可以看成一个数组
向量的生成
1、创建向量函数:
c()
2、等差数列:
seq()
seq(1, 9, 2) # 1 3 5 7 9
seq(0, 1, length.out=3) # 0.0 0.5 1.0 3、重复序列:
rep()
rep(0, 5) # 0 0 0 0 0 向量中常会用到 NA 和 NULL ,这里介绍一下这两个词语与区别:
- NA 代表的是"缺失",NULL 代表的是"不存在"。
- NA 缺失就像占位符,代表这里没有一个值,但位置存在。
- NULL 代表的就是数据不存在。
向量访问
a = c(10,20,30,40,50,60)
print(a[2])
#取出第1项到第4项,10 20 30 40
a[1:4]
#取出第1,3,5项,10 30 50
a[c(1,3,5)]
#去掉第1和第5项,20 30 40 60
a[c(-1,-5)] 可以通过下标取向量中的元素,小标从1开始
向量支持标量计算
a = c(1,2,3)
a = a - 0.5 # 0.5 1.5 2.5
b = c(1,2)
b = b ^ 2 # 1 4 向量函数
| 函数 | 说明 |
| sort(a) | 从小到大排序 |
| rev(a) | 从大到小排序 |
| order(a) | 向量排序之后的下标向量,排序后的这项在排序前的下标 |
| sum | 求和 |
| mean | 求平均值 |
| var | 方差 |
| sd | 标准差 |
| min | 最小值 |
| max | 最大值 |
| range | 取值范围(二维向量,最大值和最小值) |
| which() | a = c(1,2,3,4,5) b =a[which(a>=3 & a<=4)] # 2 3 4 |
| all() | 向量全为TRUE,返回TRUE |
| any() | 向量存在一个TRUE,返回TRUE |
5、矩阵
矩阵类似于二维数组
矩阵生成:
vector = c(1,2,3,4,5,6) # 创建向量
m = matrix(vector, 2, 3) #创建矩阵,2行3列 矩阵访问:
m[1,1] # 第1行、第1列 设置矩阵行列名称:
colnames(m) = c("x", "y", "z")
rownames(m) = c("a", "b")
x y z
a 1 2 3
b 4 5 6 矩阵乘法运算:
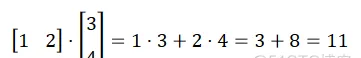
> m1 = matrix(c(1, 2), 1, 2)
> m2 = matrix(c(3, 4), 2, 1)
> m1 %*% m2
[,1]
[1,] 11 逆矩阵:
> A = matrix(c(1, 3, 2, 4), 2, 2)
> solve(A)
[,1] [,2]
[1,] -2.0 1.0
[2,] 1.5 -0.5 solve() 函数用于求解线性代数方程,基本用法是 solve(A,b),其中,A 为方程组的系数矩阵,b 方程的向量或矩阵。
> (A = matrix(c(1, 3, 2, 4), 2, 2))
[,1] [,2]
[1,] 1 2
[2,] 3 4
> apply(A, 1, sum) # 第二个参数为 1 按行操作,用 sum() 函数
[1] 3 7
> apply(A, 2, sum) # 第二个参数为 2 按列操作
[1] 4 6