主要参考内容:
1. 《Field-aware Factorization Machines for CTR Prediction》
2. 美团点评的技术文章:https://tech.meituan.com/deep-understanding-of-ffm-principles-and-practices.html
原理的话,美团这篇博文很详细(当然参考原文亦可),我这边就大致就着美团技术文章做一些阅读笔记。
一、FM模型
引用(2)文中一句话:“旨在解决稀疏数据下的特征组合问题”。先看一般的多元线性回归模型:
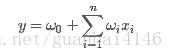
。优化的目的就是希望找到相应的权值
、以及偏置
使得目标函数损失最小。我们可以看到该模型是不考虑特征组合的(也就是缺少
的组合)。这在现实中是不符合实际的,文中的例子:"USA"和“Thanksgiving”、"China"和"Chinese New Year",这样的特征组合出现,很符合实际的需求。
接下来引入特征组合:
独热编码问题(one-hot)
很自然的,我们会遇到很多类别特征,比如很常见的:性别,国籍(目前我国是不支持双重国籍的),职业等。那么为了输入模型中,我们需要将类别特征数字化。比如性别:男、女、其他。那么男孩可以表示为(1,0,0),女孩就是(0,1,0),其他就是(0,0,1)。
题外话:独热编码后的数据是怎么输入模型训练的?
大家对one-hot的概念可以自行学习,但是独热编码的后的数据是怎么输入模型训练的呢?(虽然简单,但容易忽视的问题)。很简单,就是把一个特征变多个特征:
输入模型训练的时候就相当于整个数据集横向拉长了。很明显,我们看到数据集很稀疏了。(就是有很多0)
FM的参数训练问题
从前面的公式后半截(
)可以看到,我们希望通过训练得到参数
。现实情况是特征很稀疏,如果有很多特征x是0的话,
一组合就更有可能为0,要想训练出参数就很困难了。于是引入隐向量的概念,这是矩阵分解中的思想,具体可以查看原文资料。
至于为什么这么做更好呢,还是技术博文里的那句话引过来:
简单解释一下,举个例子,如果参数没有因子化,现在要求组合参数
,
,
。那么在求
的时候,所有特征
、
非0的样本都可以用来训练
。但实际情况是,尤其是对于类别型特征来说,这样的样本不会很多。同理,其他参数也是如此。
如果参数因子化表示,
,
,那么所有特征
,
,
非0的样本都可以用来训练
,参数间不再独立,可用于训练的样本数量大大增加。(以上是个人理解,不当处请指正)
参数训练用的梯度下降法,原理不再赘述,可自行查阅。
二、FFM的概念
ffm就是加了一个field的概念。它把相同性质的特征归于同一个field中。如下:
大致就是这样子的表示,具体可以参考原文和上面技术博文。那么引入field的概念后,参数表示有什么变化呢?下面有三个field、六个feature(年龄是数值型特征):
同一个隐参数
和其他所有特征隐参数做内积,这是fm做法。而在ffm中,每个特征对不同field都有一个隐参数:
以上是对field的直观理解。具体内容还是以原文为准。
三、FFM的实现
同样,详细内容原文包括那篇美团技术博文都有。我这里只是对我学习过程中遇到的问题做简单介绍。FFM采用的对数损失、L2惩罚项,做二元分类。伪代码(原文中的):
模型的初始化(init(tr.n,tr.m,pa))
这里很简单,没什么好说的(所有参数均已注释)。
class ffm(object):
def __init__(self, feature_num, fild_num, feature_dim_num, feat_fild_dic, learning_rate, regular_para, stop_threshold):
#n个特征,m个域,每个特征维度k
self.n = feature_num
self.m = fild_num
self.k = feature_dim_num
self.dic = feat_fild_dic
#设置超参,学习率eta, 正则化系数lamda
self.eta = learning_rate
self.lamda = regular_para
self.threshold = stop_threshold
self.w = np.random.rand(self.n, self.m , self.k) / math.sqrt(self.k)
#self.G是每轮梯度平方和
self.G = np.ones(shape = (feature_num, fild_num, feature_dim_num), dtype = np.float64)
其中feat_field_dic是一个字典,大致样式:{feature1:field,......}。也就是存储了每个feature所对应的field,这个我在数据预处理部分得到。
模型训练
这是主要部分,其中另外封装了两个函数phi()和sgd_para()。前者phi()是模型的计算函数:
这里省略了常数项和一次项。后者是梯度下降法更新参数的。后面再说,先看下整体的训练代码:
def train(self, tr_l, val_l, train_y, val_y, max_echo):
#tr_l, val_l, train_y, val_y, max_echo分别是
#训练集、验证集、训练集标签、验证集标签、最大迭代次数
minloss = 0
for i in range(max_echo):
#迭代训练,max_echo是最大迭代次数
L_val = 0
Logloss = 0
order = range(len(train_y))
#打乱顺序
random.shuffle(order)
for each_data_index in order:
#取出一条记录
tr_each_data = tr_l[each_data_index]
#phi()就是模型公式
phi = self.phi(tr_each_data)
#y_i是实际的标签值
y_i = float(train_y[each_data_index])
#下面计算梯度
g_phi = -y_i/(1 + math.exp(y_i * phi))
#下面开始用梯度下降法更新模型参数
self.sgd_para(tr_each_data, g_phi)
#接下来在验证集上进行检验,基本过程和前面一样。
for each_vadata_index, each_va_y in enumerate(val_y):
val_each_data = val_l[each_vadata_index]
phi_v = self.phi(val_each_data)
y_vai = float(each_va_y)
Logloss += -(y_vai * math.log(phi_v) + (1 - y_vai) * math.log(1 - phi_v))
Logloss = Logloss/len(val_y)
#L_val += math.log(1+math.exp(-y_vai * phi_v))
print("第%d次迭代, 验证集上的LOGLOSS:%f" %(i ,Logloss))
if minloss == 0:
#minloss存储最小的LOGLOSS
minloss = Logloss
if Logloss <= self.threshold:
#也可以认为设定阈值让程序跳断,个人需要,可以去掉。
print('小于阈值!')
break
if minloss < Logloss:
#如果下一轮迭代并没有减少LOGLOSS就break出去(early stopping)
print('early stopping')
break
每一句都有详细注释。主要说明一下我在预处理部分将数据集(tr_l、va_l)处理成的样式,整体是一个列表,每个元素是一条记录,每条记录用字典的形式存储,只存储每条记录中非0的特征值。形如:
接下来,看下刚才封装的两个函数,首先是phi():
def phi(self, tmp_dict):
#样本在这要归一化,防止计算溢出
sum_v = sum(tmp_dict.values())
#首先先找到每条数据中非0的特征的索引,放到一个列表中
phi_tmp = 0
key_list = tmp_dict.keys()
for i in range(len(key_list)):
#feat_index是特征的索引,fild_index1是域的索引,value1是特征对应的值
feat_index1 = key_list[i]
fild_index1 = self.dic[feat_index1]
#这里除以sum_v的目的就是对这条进行归一化(将所有特征取值归到0到1之间)
#当然前面已经对每个特征进行归一化了(0-1)
value1 = tmp_dict[feat_index1] / sum_v
#两个非0特征两两內积
for j in range(i+1, len(key_list)):
feat_index2 = key_list[j]
fild_index2 = self.dic[feat_index2]
value2 = tmp_dict[feat_index2] / sum_v
w1 = self.w[feat_index1, fild_index2]
w2 = self.w[feat_index2, fild_index1]
#最终的值由多有特征组合求和得到
phi_tmp += np.dot(w1, w2) * value1 * value2
return phi_tmp
这里注意那边样本归一化和特征归一化,我卡在这里很久。我把所有类别特征onehot编码后,那么这些类别特征只能取0或者1。我再把数值型特征归一化(maxmin()归一化),有的值会很小(比如0.0001)。那么样本再归一化,每个特征除以该样本的所有特征取值之和,这样都落到0~1之间了。也就是先纵向归一化再横向归一化。
再看下另外一个封装的函数sgd_para():
def sgd_para(self, tmp_dict, g_phi):
sum_v = sum(tmp_dict.values())
key_list = tmp_dict.keys()
for i in range(len(key_list)):
feat_index1 = key_list[i]
fild_index1 = self.dic[feat_index1]
value1 = tmp_dict[feat_index1] / sum_v
for j in range(i+1, len(key_list)):
feat_index2 = key_list[j]
fild_index2 = self.dic[feat_index2]
value2 = tmp_dict[feat_index2] / sum_v
w1 = self.w[feat_index1, fild_index2]
w2 = self.w[feat_index2, fild_index1]
#更新g以及G
g_feati_fildj = g_phi * value1 * value2 * w2 + self.lamda * w1
g_featj_fildi = g_phi * value1 * value2 * w1 + self.lamda * w2
self.G[feat_index1, fild_index2] += g_feati_fildj ** 2
self.G[feat_index2, fild_index1] += g_featj_fildi ** 2
#math.sqrt()只能接受一个元素,而np.sqrt()可以对整个向量开根
self.w[feat_index1, fild_index2] -= self.eta / np.sqrt(self.G[feat_index1, fild_index2]) * g_feati_fildj
self.w[feat_index2, fild_index1] -= self.eta / np.sqrt(self.G[feat_index2, fild_index1]) * g_featj_fildi
这里主要是细心点,符号不能错。尤其是正则化参数对应的参数w和计算梯度时对应的w是不同的。这里对应的计算公式就是求梯度:
学习率是用的AdaGrad算法,他会根据梯度变化的大小,自动调整学习率。更新方式如下:
这里公式里有(+1)是为了防止被除数是0的情况,而前面程序中在初始化的时候就是ones(),也就是初始化就从1开始,所以没有加一。
主要就这么多,接下来顺便看下预处理的代码:
def preprocess(tr_data, te_data, cate_list, ignore_list):
#tr_data, te_data分别是训练集和测试集pandas的dataframe表示
#cate_list, ignore_list分别是类别特征列表、以及不需要的特征列表
#先去掉不要的特征属性
tr_data.drop(ignore_list, axis=1, inplace=True)
te_data.drop(ignore_list, axis=1, inplace=True)
#print(tr_data)
# 先从训练集tr_data分出一部分作验证集,用train_test_split
X, y = tr_data.drop(["id", "target"], axis=1).values, tr_data['target'].values
X_train, X_val, y_train, y_val = train_test_split(X, y, test_size=0.25, random_state=0)
X_test = te_data.drop(["id"], axis=1).values
#到这里数据集从dataframe变成了array数组格式
tr_data.drop(["id", "target"], axis=1, inplace = True)
#去掉id和target后,未onehot编码前,可以先找到域的个数。
m = len(tr_data.columns)
#设定类别特征所在索引,也就是类别域对应的索引。
col_list = list(tr_data.columns)
cate_list_index = []
for cate_index, cate in enumerate(col_list):
if cate in cate_list:
cate_list_index.append(cate_index)
# 训练数据和测试数据连接一起做归一化
X_all = np.concatenate([X_train, X_val, X_test])
# 先将所有类别属性序列化
lb = LabelEncoder()
for i in cate_list_index:
lb.fit(X_all[:, i])
X_all[:, i] = lb.transform(X_all[:, i])
X_train[:, i] = lb.transform(X_train[:, i])
X_val[:, i] = lb.transform(X_val[:, i])
X_test[:, i] = lb.transform(X_test[:, i])
# 接下来对数值型数据进行归一化,这里用最大最小归一,先设置数值型特征的索引列表
del lb
#对非类别行进行归一化
for i in range(len(col_list)):
if i not in cate_list_index:
minv = X_all[:, i].min()
maxv = X_all[:, i].max()
delta = maxv - minv
X_all[:, i] = (X_all[:, i] - minv) / delta
X_train[:, i] = (X_train[:, i] - minv)/ delta
X_val[:, i] = (X_val[:, i] - minv)/ delta
X_test[:, i] = (X_test[:, i] - minv)/ delta
#进行onhot编码
enc = OneHotEncoder(categorical_features = cate_list_index)
enc.fit(X_all)
gc.collect()
#拟合完的enc,可以输出每个类别特征取值个数列表
m_list = list(enc.n_values_)
#onehot编码以后,数据就会很稀疏,直接toarray会报内存错误。coo_matix
X_all = enc.transform(X_all)
#onehot编码后,可以输出特征的个数了。onehot以后非类别的特征顺次靠后。
n = X_all.get_shape()[1]
dic = dict()
h = 0
cate_list_index = range(len(cate_list_index))
for i in range(m):
if i in cate_list_index:
for j in range(m_list[0]):
dic[h] = i
h += 1
m_list.pop(0)
else:
dic[h] = i
h += 1
X_train = enc.transform(X_train)
X_val = enc.transform(X_val)
X_test = enc.transform(X_test)
#接下来调用封装的函数将非0矩阵转成前面列表中套字典的形式
X_train = generate_li(X_train)
X_val = generate_li(X_val)
X_test = generate_li(X_test)
return X_train, X_val, X_test, y_train, y_val, n, m, dic
值得注意的是,直接把非零矩阵存储coo_matrix转成矩阵的话,会内存溢出。也可以看出数据onehot后是多么稀疏。
另一个,onehot后的类别特征顺次靠前,数值型顺次靠后(这个可以查官方文档)。
我整体预处理的过程就是
1. 数据拆成训练、验证、测试集 2. 对类别特征(field)标签化 3. 对数值型特征(field)归一化 4.对类别特征(field)独热编码
其中封装的一个函数gnerate_li()是用来将原来的稀疏矩阵存储转成前面需要的列表套字典的那种格式的。具体代码如下:
def generate_li(m):
r = list(m.row)
c = list(m.col)
value = list(m.data)
l = [dict() for i in range(m.get_shape()[0])]
for i,v in enumerate(r):
x = c[i]
l[v][x] = value[i]
return l
这里很简单,不做赘述。感兴趣的话,可以去看下python中稀疏矩阵存储方式,有很多种,这里onehot后默认是最简单的一种coo_matrix。
对了,一开始我是转成列表的,所以每次计算都要扫描一次列表,比较费时,还是字典查询快。
原文中对模型训练的时候用了无锁多线程,参考文章:
《HOGWILD!: A Lock-Free Approach to Parallelizing Stochastic Gradient Descent》。
我没有实现这种方法。python中的多线程是有限制的,因为python解释型语言,依赖解释器,解释器运行代码的时候会给每个线程加个GIL锁,每100行释放一次,让别的线程有机会运行。这样效率降低了。不知道文中是不是有新颖的方法(时间问题我没有看)
我用了python中的多进程的方法。原本单进程训练迭代2次是差不多三个多小时,用了多进程缩小到25分钟左右。这边下篇会说明。
不当之处,还请指正。