主要參考内容:
1. 《Field-aware Factorization Machines for CTR Prediction》
2. 美團點評的技術文章:https://tech.meituan.com/deep-understanding-of-ffm-principles-and-practices.html
原理的話,美團這篇博文很詳細(當然參考原文亦可),我這邊就大緻就着美團技術文章做一些閱讀筆記。
一、FM模型
引用(2)文中一句話:“旨在解決稀疏資料下的特征組合問題”。先看一般的多元線性回歸模型:
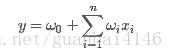
。優化的目的就是希望找到相應的權值
、以及偏置
使得目标函數損失最小。我們可以看到該模型是不考慮特征組合的(也就是缺少
的組合)。這在現實中是不符合實際的,文中的例子:"USA"和“Thanksgiving”、"China"和"Chinese New Year",這樣的特征組合出現,很符合實際的需求。
接下來引入特征組合:
獨熱編碼問題(one-hot)
很自然的,我們會遇到很多類别特征,比如很常見的:性别,國籍(目前我國是不支援雙重國籍的),職業等。那麼為了輸入模型中,我們需要将類别特征數字化。比如性别:男、女、其他。那麼男孩可以表示為(1,0,0),女孩就是(0,1,0),其他就是(0,0,1)。
題外話:獨熱編碼後的資料是怎麼輸入模型訓練的?
大家對one-hot的概念可以自行學習,但是獨熱編碼的後的資料是怎麼輸入模型訓練的呢?(雖然簡單,但容易忽視的問題)。很簡單,就是把一個特征變多個特征:
輸入模型訓練的時候就相當于整個資料集橫向拉長了。很明顯,我們看到資料集很稀疏了。(就是有很多0)
FM的參數訓練問題
從前面的公式後半截(
)可以看到,我們希望通過訓練得到參數
。現實情況是特征很稀疏,如果有很多特征x是0的話,
一組合就更有可能為0,要想訓練出參數就很困難了。于是引入隐向量的概念,這是矩陣分解中的思想,具體可以檢視原文資料。
至于為什麼這麼做更好呢,還是技術博文裡的那句話引過來:
簡單解釋一下,舉個例子,如果參數沒有因子化,現在要求組合參數
,
,
。那麼在求
的時候,所有特征
、
非0的樣本都可以用來訓練
。但實際情況是,尤其是對于類别型特征來說,這樣的樣本不會很多。同理,其他參數也是如此。
如果參數因子化表示,
,
,那麼所有特征
,
,
非0的樣本都可以用來訓練
,參數間不再獨立,可用于訓練的樣本數量大大增加。(以上是個人了解,不當處請指正)
參數訓練用的梯度下降法,原理不再贅述,可自行查閱。
二、FFM的概念
ffm就是加了一個field的概念。它把相同性質的特征歸于同一個field中。如下:
大緻就是這樣子的表示,具體可以參考原文和上面技術博文。那麼引入field的概念後,參數表示有什麼變化呢?下面有三個field、六個feature(年齡是數值型特征):
同一個隐參數
和其他所有特征隐參數做内積,這是fm做法。而在ffm中,每個特征對不同field都有一個隐參數:
以上是對field的直覺了解。具體内容還是以原文為準。
三、FFM的實作
同樣,詳細内容原文包括那篇美團技術博文都有。我這裡隻是對我學習過程中遇到的問題做簡單介紹。FFM采用的對數損失、L2懲罰項,做二進制分類。僞代碼(原文中的):
模型的初始化(init(tr.n,tr.m,pa))
這裡很簡單,沒什麼好說的(所有參數均已注釋)。
class ffm(object):
def __init__(self, feature_num, fild_num, feature_dim_num, feat_fild_dic, learning_rate, regular_para, stop_threshold):
#n個特征,m個域,每個特征次元k
self.n = feature_num
self.m = fild_num
self.k = feature_dim_num
self.dic = feat_fild_dic
#設定超參,學習率eta, 正則化系數lamda
self.eta = learning_rate
self.lamda = regular_para
self.threshold = stop_threshold
self.w = np.random.rand(self.n, self.m , self.k) / math.sqrt(self.k)
#self.G是每輪梯度平方和
self.G = np.ones(shape = (feature_num, fild_num, feature_dim_num), dtype = np.float64)
其中feat_field_dic是一個字典,大緻樣式:{feature1:field,......}。也就是存儲了每個feature所對應的field,這個我在資料預處理部分得到。
模型訓練
這是主要部分,其中另外封裝了兩個函數phi()和sgd_para()。前者phi()是模型的計算函數:
這裡省略了常數項和一次項。後者是梯度下降法更新參數的。後面再說,先看下整體的訓練代碼:
def train(self, tr_l, val_l, train_y, val_y, max_echo):
#tr_l, val_l, train_y, val_y, max_echo分别是
#訓練集、驗證集、訓練集标簽、驗證集标簽、最大疊代次數
minloss = 0
for i in range(max_echo):
#疊代訓練,max_echo是最大疊代次數
L_val = 0
Logloss = 0
order = range(len(train_y))
#打亂順序
random.shuffle(order)
for each_data_index in order:
#取出一條記錄
tr_each_data = tr_l[each_data_index]
#phi()就是模型公式
phi = self.phi(tr_each_data)
#y_i是實際的标簽值
y_i = float(train_y[each_data_index])
#下面計算梯度
g_phi = -y_i/(1 + math.exp(y_i * phi))
#下面開始用梯度下降法更新模型參數
self.sgd_para(tr_each_data, g_phi)
#接下來在驗證集上進行檢驗,基本過程和前面一樣。
for each_vadata_index, each_va_y in enumerate(val_y):
val_each_data = val_l[each_vadata_index]
phi_v = self.phi(val_each_data)
y_vai = float(each_va_y)
Logloss += -(y_vai * math.log(phi_v) + (1 - y_vai) * math.log(1 - phi_v))
Logloss = Logloss/len(val_y)
#L_val += math.log(1+math.exp(-y_vai * phi_v))
print("第%d次疊代, 驗證集上的LOGLOSS:%f" %(i ,Logloss))
if minloss == 0:
#minloss存儲最小的LOGLOSS
minloss = Logloss
if Logloss <= self.threshold:
#也可以認為設定門檻值讓程式跳斷,個人需要,可以去掉。
print('小于門檻值!')
break
if minloss < Logloss:
#如果下一輪疊代并沒有減少LOGLOSS就break出去(early stopping)
print('early stopping')
break
每一句都有詳細注釋。主要說明一下我在預處理部分将資料集(tr_l、va_l)處理成的樣式,整體是一個清單,每個元素是一條記錄,每條記錄用字典的形式存儲,隻存儲每條記錄中非0的特征值。形如:
接下來,看下剛才封裝的兩個函數,首先是phi():
def phi(self, tmp_dict):
#樣本在這要歸一化,防止計算溢出
sum_v = sum(tmp_dict.values())
#首先先找到每條資料中非0的特征的索引,放到一個清單中
phi_tmp = 0
key_list = tmp_dict.keys()
for i in range(len(key_list)):
#feat_index是特征的索引,fild_index1是域的索引,value1是特征對應的值
feat_index1 = key_list[i]
fild_index1 = self.dic[feat_index1]
#這裡除以sum_v的目的就是對這條進行歸一化(将所有特征取值歸到0到1之間)
#當然前面已經對每個特征進行歸一化了(0-1)
value1 = tmp_dict[feat_index1] / sum_v
#兩個非0特征兩兩內積
for j in range(i+1, len(key_list)):
feat_index2 = key_list[j]
fild_index2 = self.dic[feat_index2]
value2 = tmp_dict[feat_index2] / sum_v
w1 = self.w[feat_index1, fild_index2]
w2 = self.w[feat_index2, fild_index1]
#最終的值由多有特征組合求和得到
phi_tmp += np.dot(w1, w2) * value1 * value2
return phi_tmp
這裡注意那邊樣本歸一化和特征歸一化,我卡在這裡很久。我把所有類别特征onehot編碼後,那麼這些類别特征隻能取0或者1。我再把數值型特征歸一化(maxmin()歸一化),有的值會很小(比如0.0001)。那麼樣本再歸一化,每個特征除以該樣本的所有特征取值之和,這樣都落到0~1之間了。也就是先縱向歸一化再橫向歸一化。
再看下另外一個封裝的函數sgd_para():
def sgd_para(self, tmp_dict, g_phi):
sum_v = sum(tmp_dict.values())
key_list = tmp_dict.keys()
for i in range(len(key_list)):
feat_index1 = key_list[i]
fild_index1 = self.dic[feat_index1]
value1 = tmp_dict[feat_index1] / sum_v
for j in range(i+1, len(key_list)):
feat_index2 = key_list[j]
fild_index2 = self.dic[feat_index2]
value2 = tmp_dict[feat_index2] / sum_v
w1 = self.w[feat_index1, fild_index2]
w2 = self.w[feat_index2, fild_index1]
#更新g以及G
g_feati_fildj = g_phi * value1 * value2 * w2 + self.lamda * w1
g_featj_fildi = g_phi * value1 * value2 * w1 + self.lamda * w2
self.G[feat_index1, fild_index2] += g_feati_fildj ** 2
self.G[feat_index2, fild_index1] += g_featj_fildi ** 2
#math.sqrt()隻能接受一個元素,而np.sqrt()可以對整個向量開根
self.w[feat_index1, fild_index2] -= self.eta / np.sqrt(self.G[feat_index1, fild_index2]) * g_feati_fildj
self.w[feat_index2, fild_index1] -= self.eta / np.sqrt(self.G[feat_index2, fild_index1]) * g_featj_fildi
這裡主要是細心點,符号不能錯。尤其是正則化參數對應的參數w和計算梯度時對應的w是不同的。這裡對應的計算公式就是求梯度:
學習率是用的AdaGrad算法,他會根據梯度變化的大小,自動調整學習率。更新方式如下:
這裡公式裡有(+1)是為了防止被除數是0的情況,而前面程式中在初始化的時候就是ones(),也就是初始化就從1開始,是以沒有加一。
主要就這麼多,接下來順便看下預處理的代碼:
def preprocess(tr_data, te_data, cate_list, ignore_list):
#tr_data, te_data分别是訓練集和測試集pandas的dataframe表示
#cate_list, ignore_list分别是類别特征清單、以及不需要的特征清單
#先去掉不要的特征屬性
tr_data.drop(ignore_list, axis=1, inplace=True)
te_data.drop(ignore_list, axis=1, inplace=True)
#print(tr_data)
# 先從訓練集tr_data分出一部分作驗證集,用train_test_split
X, y = tr_data.drop(["id", "target"], axis=1).values, tr_data['target'].values
X_train, X_val, y_train, y_val = train_test_split(X, y, test_size=0.25, random_state=0)
X_test = te_data.drop(["id"], axis=1).values
#到這裡資料集從dataframe變成了array數組格式
tr_data.drop(["id", "target"], axis=1, inplace = True)
#去掉id和target後,未onehot編碼前,可以先找到域的個數。
m = len(tr_data.columns)
#設定類别特征所在索引,也就是類别域對應的索引。
col_list = list(tr_data.columns)
cate_list_index = []
for cate_index, cate in enumerate(col_list):
if cate in cate_list:
cate_list_index.append(cate_index)
# 訓練資料和測試資料連接配接一起做歸一化
X_all = np.concatenate([X_train, X_val, X_test])
# 先将所有類别屬性序列化
lb = LabelEncoder()
for i in cate_list_index:
lb.fit(X_all[:, i])
X_all[:, i] = lb.transform(X_all[:, i])
X_train[:, i] = lb.transform(X_train[:, i])
X_val[:, i] = lb.transform(X_val[:, i])
X_test[:, i] = lb.transform(X_test[:, i])
# 接下來對數值型資料進行歸一化,這裡用最大最小歸一,先設定數值型特征的索引清單
del lb
#對非類别行進行歸一化
for i in range(len(col_list)):
if i not in cate_list_index:
minv = X_all[:, i].min()
maxv = X_all[:, i].max()
delta = maxv - minv
X_all[:, i] = (X_all[:, i] - minv) / delta
X_train[:, i] = (X_train[:, i] - minv)/ delta
X_val[:, i] = (X_val[:, i] - minv)/ delta
X_test[:, i] = (X_test[:, i] - minv)/ delta
#進行onhot編碼
enc = OneHotEncoder(categorical_features = cate_list_index)
enc.fit(X_all)
gc.collect()
#拟合完的enc,可以輸出每個類别特征取值個數清單
m_list = list(enc.n_values_)
#onehot編碼以後,資料就會很稀疏,直接toarray會報記憶體錯誤。coo_matix
X_all = enc.transform(X_all)
#onehot編碼後,可以輸出特征的個數了。onehot以後非類别的特征順次靠後。
n = X_all.get_shape()[1]
dic = dict()
h = 0
cate_list_index = range(len(cate_list_index))
for i in range(m):
if i in cate_list_index:
for j in range(m_list[0]):
dic[h] = i
h += 1
m_list.pop(0)
else:
dic[h] = i
h += 1
X_train = enc.transform(X_train)
X_val = enc.transform(X_val)
X_test = enc.transform(X_test)
#接下來調用封裝的函數将非0矩陣轉成前面清單中套字典的形式
X_train = generate_li(X_train)
X_val = generate_li(X_val)
X_test = generate_li(X_test)
return X_train, X_val, X_test, y_train, y_val, n, m, dic
值得注意的是,直接把非零矩陣存儲coo_matrix轉成矩陣的話,會記憶體溢出。也可以看出資料onehot後是多麼稀疏。
另一個,onehot後的類别特征順次靠前,數值型順次靠後(這個可以查官方文檔)。
我整體預處理的過程就是
1. 資料拆成訓練、驗證、測試集 2. 對類别特征(field)标簽化 3. 對數值型特征(field)歸一化 4.對類别特征(field)獨熱編碼
其中封裝的一個函數gnerate_li()是用來将原來的稀疏矩陣存儲轉成前面需要的清單套字典的那種格式的。具體代碼如下:
def generate_li(m):
r = list(m.row)
c = list(m.col)
value = list(m.data)
l = [dict() for i in range(m.get_shape()[0])]
for i,v in enumerate(r):
x = c[i]
l[v][x] = value[i]
return l
這裡很簡單,不做贅述。感興趣的話,可以去看下python中稀疏矩陣存儲方式,有很多種,這裡onehot後預設是最簡單的一種coo_matrix。
對了,一開始我是轉成清單的,是以每次計算都要掃描一次清單,比較費時,還是字典查詢快。
原文中對模型訓練的時候用了無鎖多線程,參考文章:
《HOGWILD!: A Lock-Free Approach to Parallelizing Stochastic Gradient Descent》。
我沒有實作這種方法。python中的多線程是有限制的,因為python解釋型語言,依賴解釋器,解釋器運作代碼的時候會給每個線程加個GIL鎖,每100行釋放一次,讓别的線程有機會運作。這樣效率降低了。不知道文中是不是有新穎的方法(時間問題我沒有看)
我用了python中的多程序的方法。原本單程序訓練疊代2次是差不多三個多小時,用了多程序縮小到25分鐘左右。這邊下篇會說明。
不當之處,還請指正。