方程的根的求法——交叉法,迭代法
迭代法
一、迭代法基本原理介绍
-
迭代法的基本思想
将方程改写成某种等价形式,由等价形式构造出相应的迭代公式,然后选择方程的某个初始近似根x_0,代入迭代公式,反复矫正,逼近所求的根的近似值,直到达到满足的精度为止。
给定一个方程f(x)=0,要求求出这个方程的一个近似的根。我们给出计算过程:
- 将方程改写成为x=g(x)的等价形式。比如改写成:x=x+f(x)②(右边的x+f(x)就相当于g(x))。
- 给定一个初值x_0代入②式的右端,得到x_1=g(x_0 ),x_2=g(x_1 ),x3=g(x_2)……
- 通过(2),本质是一个递推式,即上述的迭代公式:x_(k+1)=g(x_k ),k=0,1,2,3……进而我们得到一个序列{x_k },即{x_0,x_1,x_2……x_k……}。
- 如果序列{x_k}有极限x*,那么x*即是所求的方程的近似根。或者说按照所给的精度(比如0.001)如果偏差|x_(k+1)-x_k|<ε,ε≤0.001,那么就保证了迭代误差|x-x_k|足够小。因此|x_(k+1)-x_k|<ε往往作为迭代结束的条件。
-
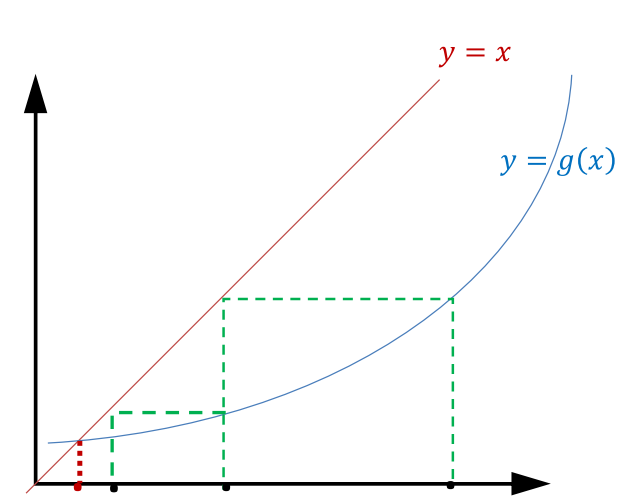
此方法的几何意义:
y=x与y=g(x)的图像的交点——
数值计算方法——第一节方程的根的求解方程的根的求法——交叉法,迭代法 -
给出一个例子:求方程:x^3-x-1=0的根
我们将上述方程改写成为它的一个等价形式:x=∛(x+1)
选择初始值x_0=1.5
4. 关于迭代法中g(x)的选择的问题
虽然迭代法的思想简单,但是并不是每次都能得到根的值:g(x)的选择是关键点。还是以方程x^3-x-1=0为例,假如我们将方程改写成为另外一种形式:
我们仍取初值x_0=1.5,然后建立迭代公式:
经过迭代我们发现𝑥1=2.375,𝑥2=12.3976……一直迭代下去并没有发现序列收敛。所以𝑔(𝑥)的选择是很重要的。
有定理:设方程x=g(x),在(a,b)内有根x,满足李普希兹(Lipschitz)条件:即对(a,b)内任意的x_1,x_2 都有:
其中q为一个确定的正数,且q<1。那么方程在(a, b)内有唯一的根。
且迭代公式:
对于任意初始近似值x_0均收敛于方程的根x
需要说明三点:
①要验证g(x)满足李普希兹条件是比较困难的,若g(x)可微,可以利用充分条件
来替代李普希兹条件。否则不一定能满足求出收敛的根x*。
②迭代的终止条件:|x_(k+1)-x_k|<ε。
③在上面我们已经说过,确定g(x)是比较重要的。选取不当的话,迭代的结果不会收敛。最一般地,g(x)可以写成这种形式:
x+α(x)f(x);
即方程x=x+α(x)f(x)的形式,这样可以通过选取α(x),使其满足①中给出的充分条件。
二、常用的确定g(x)的方法
1.牛顿法(Newton-Raphson Method)
(1)在牛顿法中,我们选择
(2)迭代公式:
(3)牛顿法确定g(x)的几何意义:做x_0这点的切线,切线与x轴交点为x_1,后面以此类推……
2.弦截法(Secant Method)
(1)在弦截法中,递推公式为:
交叉法
一、交叉法概述
这是一类求根方法,对于连续的𝑓(𝑥), 现在已知𝑓(x_1)𝑓(x_2) < 0,那么在x_1与x_2之间一定有一点𝑥满足𝑓(𝑥) = 0,即 𝑥 ∈ (x_1, x_2),(这里不妨设x_1 < x_2) 我们可通过不断减小这个区间的范围,从而找到𝑥的数值解。
二、 交叉法的具体方法
- 逐步求根法
- 二分法
- 比例求根法
方法过程:
- 设𝑓(𝑎) < 0, 𝑓(𝑏) > 0
-
对于上述的三种方法:
逐步求根法:
c=a+h (h为步长)
二分法:
c=(a+b)/2
比例求根法:
数值计算方法——第一节方程的根的求解方程的根的求法——交叉法,迭代法 -
计算𝑓(c)
若𝑓(c)> 0,则令a=c
若𝑓(c)< 0, 则令b=c
若𝑓(c)= 0, 则x=c,结束
- 返回步骤2
三、例题分析
例1:分别用二分法、牛顿法、弦截法求下列方程的根,并分别画出几种方法所求根的收敛速 度对比图(即画出相对误差随迭代步数的变化趋势图)以下给出Matlab代码。
- f(x)=cosx-x
function y=f(x)
%编辑方程式
y=cos(x)-x;
①二分法:
function [c,k,iteration]=half(a,b,epsilon)
%默认取中点为数值解
iteration=zeros(19,1);
k=0;%迭代次数
result=test;
% result是零点,即方程的解
myResult=0;
c=0;
while(abs(myResult-result)>epsilon)
c=(a+b)/2;
if f(a)*f(c)<0
b=c;
elseif f(b)*f(c)<0
a=c;
end
myResult=c;
k=k+1;
iteration(k)=abs(myResult-result)/result;
end
x=1:k;
plot(x,iteration,'-b');
grid on
xlabel('迭代次数');
ylabel('相对误差');
legend('二分法求解');
②牛顿法
function [k,x1]=newton(x0,epsilon)
%牛顿法求根
result=test;
%result为根的值;
syms x
g=cos(x)-x;
f1=subs(diff(g),x,x0);
x1=x0-f(x0)/f1;
k=1;
iterater=zeros(5,1);
while (abs(x0-x1)>=epsilon)
x0=x1;
f1=subs(diff(g),x,x0);
x1=x0-f(x0)/f1;
myResult=x1;
iterater(k)=abs(myResult-result)/result;
k=k+1;
end
k1=1:k;
plot(k1,iterater,'-.r')
③ 弦截法
function secant(x0,x1,epsilon)
%弦截法求根
x2=x1-(x1-x0)*f(x1)/(f(x1)-f(x0));
k=1;
while(abs(x2-x1)>=epsilon)
x0=x1;
x1=x2;
x2=x1-(x1-x0)*f(x1)/(f(x1)-f(x0));
end
k
x2