【高等数学】重积分

二重积分的概念与性质

一、二重积分的定义

设$f(x,y)$是有界闭区域$D$上的有界函数，将闭区域$D$任意分成$n$哥小闭区域$\Delta\sigma_1,\Delta\sigma_2,\cdots,\Delta\sigma_n$，其中$\Delta\sigma_i$表示第$i$个小闭区域，也表示它的面积，在每个$\Delta\sigma_i$上任取一点$(\xi_i,\eta_i)\Delta\sigma_i\quad(i=1,2,3,\cdots,n)$，并作和$\sum^{n}{i=1}f(\xi_i,\eta_i)\Delta\sigma_i$，如果当各小闭区域的直径中的最大值$\lambda\to0$时，这个和的极限总存在，且与闭区域$D$的分发及点$(\xi_i,\eta_i)$的取法无关，那么称此极限为函数$f(x,y)$在闭区域$D$上的二重积分，记作$\begin{aligned}\iint\limits{D}f(x,y)d\sigma=\lim_{\lambda\to0}\sum^n_{i=1}f(\xi_i,\eta_i)\Delta\sigma_i\end{aligned}$，其中$f(x,y)d\sigma$叫做被积表达式，$x$与$y$叫做积分变量，$D$叫做积分区域，$\sum^n_{i=1}f(\xi_i,\eta_i)\Delta\sigma_i$叫做积分和

二、二重积分的性质

性质1（线性）：设$\alpha$与$\beta$为常数，则$\iint\limits_D[\alpha f(x,y)+\beta g(x,y)]d\sigma=\alpha\iint\limits_Df(x,y)d\sigma+\beta\iint\limits_Dg(x,y)d\sigma$

性质2（区域可加）：如果闭区域$D$被有线条曲线分成有限个部分闭区域，那么在$D$上的二重积分等于在各部分闭区域上的二重积分的和

例：如果$D$分成两个闭区域$D_1$与$D_2$，则$\iint\limits_Df(x,y)d\sigma=\iint\limits_{D_1}f(x,y)d\sigma+\iint\limits_{D_2}f(x,y)d\sigma$

性质3：如果在$D$上，$f(x,y)=1$，$\sigma$是$D$的面积，那么$\sigma=\iint\limits_D1d\sigma=\iint\limits_Dd\sigma$

性质4：如果在$D$上，$f(x,y)\leq g(x,y)$，那么有$\iint\limits_Df(x,y)d\sigma\leq\iint\limits_Dg(x,y)d\sigma$。特殊地，由于$-|f(x,y)|\leq f(x,y)\leq|f(x,y)|$，所以$|\iint\limits_Df(x,y)d\sigma|\leq\iint\limits_D|f(x,y)|d\sigma$

性质5：设$M$和$m$分别是$f(x,y)$在闭区域$D$上的最大值和最小值，$\sigma$是$D$的面积，则有$m\sigma\leq\iint\limits_Df(x,y)d\sigma\leq M\sigma$

证明：

设$m\leq f(x,y)\leq M$

由性质4知，$\iint\limits_Dmd\sigma\leq\iint\limits_Df(x,y)d\sigma\leq\iint\limits_DMd\sigma$，即$m\iint\limits_Dd\sigma\leq\iint\limits_Df(x,y)d\sigma\leq M\iint\limits_Dd\sigma$

由性质3得，$m\sigma\leq\iint\limits_Df(x,y)d\sigma\leq M\sigma$

证毕

性质6（二重积分的中值定理）：设函数$f(x,y)$在闭区域$D$上连续，$\sigma$是$D$的面积，则在$D$上至少存在一点$(\xi_i,\eta_i)$，使得$\iint\limits_Df(x,y)d\sigma=f(\xi,\eta)\cdot\sigma$

证明：

$\sigma\ne0$

由性质5知，两边同除$\sigma$得，$m\leq\frac1\sigma\iint\limits_Df(x.y)d\sigma\leq M$

又$\because f(x,y)$在区域$D$上连续

由闭区域连续函数的介值定理可知，在区域$D$上至少存在一点$(\xi,\eta)$

使$f(\xi,\eta)=\frac1\sigma\iint\limits_Df(x,y)d\sigma$

即$\iint\limits_Df(x,y)d\sigma=f(\xi,\eta)\cdot\sigma$

二重积分的计算法

一、利用直角坐标计算二重积分

1. $X$型区域

区域$D$由$\begin{cases}y_1(x)\leq y\leq y_2(x)\a\leq x\leq b\end{cases}$确定

1. 先确定$x$的范围
2. 再任取$x$，沿$y$轴的正方向穿针，穿入为下限，穿出为上限

$\iint\limits_Df(x,y)d\sigma=\int^b_adx\int^{y_2(x)}_{y_1(x)}f(x,y)dy$

2. $Y$型区域

区域$D$由$\begin{cases}x_1(y)\leq x\leq x_2(y)\c\leq y\leq d\end{cases}$确定

1. 先确定$y$的范围
2. 再任取$y$，沿$x$轴的正方向穿针，穿入为下限，穿出为上限

$\iint\limits_Df(x,y)d\sigma=\int^d_cdy\int^{x_2(y)}_{x_1(y)}f(x,y)dx$

例1：计算$\iint\limits_Dxyd\sigma$，其中$D$是由抛物线$y^2=x$及直线$y=x-2$所围成的闭区域

ax = plt.gca()

ax.spines['right'].set_color('none')

ax.spines['top'].set_color('none')

ax.spines['bottom'].set_position(('data', 0))

ax.spines['left'].set_position(('data',0))

ax.set_aspect(1)

plt.rcParams['figure.figsize']=(8,6)

X=np.arange(-5,5,0.002)

f1=lambda x:x-2

f2=lambda x:x**0.5

f3=lambda x:-x**0.5

s1=pd.Series(f1(X),index=X)

s2=pd.Series(f2(X),index=X)

s3=pd.Series(f3(X),index=X)

s1.plot()

s2.plot(color='orange')

s3.plot(color='orange')

plt.ylim(-2,3)

plt.xlim(-1,5)

           

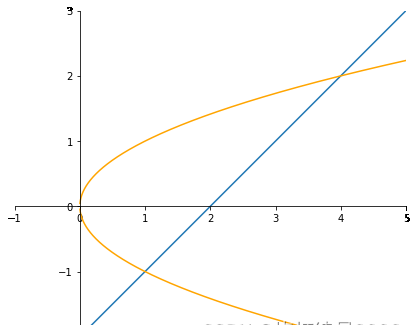
联立$\begin{cases}y^2=x\y=x-2\end{cases}$解得$\begin{cases}x=1\y=-1\end{cases}\quad\begin{cases}x=4\y=2\end{cases}$

先$y$后$x$

原式$\begin{aligned}=\int^1_0dx\int^{\sqrt x}{-\sqrt x}xydy+\int^4_1dx\int^{\sqrt x}{x-2}xydy=\frac{45}8\end{aligned}$

先$x$后$y$

$\begin{aligned}\text{原式}&=\int^2_{-1}dy\int^{y+2}{y^2}xydx\&=\int^2{-1}(\frac12yx^2)\Big|^{y+2}{y^2}dy\&=\frac12\int^2{-1}(y^3+4y^2+4y-y^5)dy\&=\frac{45}8\end{aligned}$

二、利用极坐标计算二重积分

适用情况：一般适用于圆域、部分圆域，被积函数有$(x^2+y^2)$的函数

极坐标的做法：

$\begin{cases}x=r\cdot\cos\theta\y=r\cdot\sin\theta\end{cases}\quad\begin{cases}\alpha\leq\theta\leq\beta\r_1(\theta)\leq r\leq r_2(\theta)\end{cases}$

$\begin{aligned}\iint\limits_Df(x,y)d\sigma=\int^\beta_\alpha\theta\int^{r_2(\theta)}_{r_1(\theta)}f(r\cos\theta,r\sin\theta)rdr\end{aligned}$

其中$d\sigma=dxdy=r\cdot d\theta dr$

若积分区域$D$包含原点，则$r$的下限一定为$0$

例2：计算$\iint\limits_D\arctan\frac yxd\sigma$其中$D$是由圆周$x^2+y^2=4,x^2+y^2=1$及直线$y=0,y=x$所围成的在第一象限的闭区域

ax=plt.gca()

ax.spines['right'].set_color('none')

ax.spines['top'].set_color('none')

ax.spines['bottom'].set_position(('data', 0))

ax.spines['left'].set_position(('data',0))

ax.set_aspect(1)

plt.rcParams['figure.figsize']=(8,6)

X1=np.linspace(0,2,50)

# np.arange会出现x取不到端点值，改用np.linspace

print(X1)

f1=lambda x:(4-x**2)**0.5

X2=np.linspace(0,1,50)

f2=lambda x:(1-x**2)**0.5

s1=pd.Series(f1(X1),index=X1)

s2=pd.Series(f2(X2),index=X2)

s1.plot()

s2.plot(color='orange')

           

$\begin{aligned}\text{原式}&=\int^{\frac\pi4}_0d\theta\int^2_1\arctan\frac{r\sin\theta}{r\cos\theta}rdr\&=\int^{\frac\pi4}_0d\theta\int^2_1\arctan(\tan\theta)rdr\&=\int^{\frac\pi4}_0\theta d\theta\int^2_1rdr\&=(\frac12\theta^2)\Big|^\frac\pi4_0(\frac12r^2)\Big|^2_1\&=\frac3{64}\pi^2\end{aligned}$

三重积分

一、三重积分的概念

定义：设$f(x,y,z)$是空间有界闭区域$\Omega$上的有界函数。将$\Omega$任意分成$n$个小闭区域$\Delta v_1,\Delta v_2,\cdots,\Delta v_n$，其中$\Delta v_i$表示第$i$个小闭区域，也表示它的体积。在每个$\Delta v_i$上任取一点$(\xi_i,\eta_i,\zeta_i)$，作乘积$f(\xi_i,\eta_i,\zeta_i)\Delta v_i\quad(i=1,2,\cdots,n)$，并作和$\sum^n_{i=1}f(\xi_i,\eta_i,\zeta_i)\Delta v_i$。如果当各小闭区域直径中的最大值$\lambda\to0$时，这个和的极限总存在，且与闭区域$\Omega$的分法及点$(\xi_i,\eta_i,\zeta_i)$的取法无关，那么称此极限为函数$f(x,y,z)$在闭区域$\Omega$上的三重积分，记作$\iiint\limits_\Omega f(x,y,z)dv$，即$\iiint\limits_\Omega f(x,y,z)dv=\lim_{\lambda\to0}\sum^n_{i=1}f(\xi_i,\eta_i,\zeta_i)\Delta v_i$，其中$f(x,y,z)$叫做被积函数，$dv$叫做体积函数，$\Omega$叫做积分区域

二、三重积分的计算

1. 利用直角坐标计算

先一后二（投影法）

方法

1. 先投影，确定$(x,y)$范围
2. 再任取$(x,y)$，沿$z$轴正方向穿针，确定$z$的范围，传入为下限，穿出为上限。则$\iiint\limits_\Omega f(x,y,z)dv=\iint\limits_{D_{xy}}dxdy\int^{z_2(x,y)}_{z_1(x,y)}f(x,y,z)dz$

先二后一（截面法）

方法

1. 先确定$z$的范围
2. 再任取$z$做截面，确定$(x,y)$的范围。则$\iiint\limits_\Omega f(x,y,z)dv=\int^b_adz\iint\limits_{D_{xy}}f(x,y,z)dxdy$

例1：计算三重积分$\iiint\limits_\Omega xdxdydz$，其中$\Omega$为三个坐标面及平面$x+2y+z=1$所围成的闭区域

先一后二

$\begin{aligned}\iiint\limits_\Omega xdxdydz&=\iint\limits_{D_{xy}}xdxdy\int^{1-x-2y}0dz\&=\iint\limits{D_{xy}}x(1-x-2y)dxdy\&=\int^1_0dx\int^{\frac12-\frac x2}_0(x-x^2-2xy)dy\&=\frac14\int^1_0(x-2x^2+x^3)dx\&=\frac1{48}\end{aligned}$

先二后一

$\begin{aligned}\iiint\limits_\Omega xdxdydz&=\int^1_0dz\iint\limits_{D_z}xdxdy\&=\int^1_0dz\int^{1-z}_0dx\int^{\frac12(1-x-z)}_0xdy\&=\frac1{48}\end{aligned}$

取高度为$z$的投影（此时$z$为常数），用截面确定$(x,y)$范围。

将该截面向$xoy$平面做投影，易得x的范围为$[1,z]$，由于$z$为常数，所以此时的斜线方程即为$x+2y+z=1$，可得$y$的范围为$[0,\frac12(1-x-z)]$

二、利用柱坐标计算

无论是利用柱坐标还是球坐标，由于已经将$x,y,z$替换掉了，所以整个式子中不能再出现$x,y,z$，包括积分上下限

适用于$\Omega$为圆柱（$x^2+y^2=a^2$），圆锥（$z=a\sqrt{x^2+y^2}$），旋转抛物面（$z=a(x^2+y^2)$），被积函数有$(x^2+y^2)$

令$\begin{cases}x=r\cos\theta\y=r\sin\theta\z=z\end{cases}$，则$dv=d\theta rdrdz$

例2：利用柱坐标计算三重积分$\iiint\limits_\Omega zdxdydz$，其中$\Omega$是由曲面$z=x^2+y^2$与平面$z=4$所围成的闭区域

$\begin{aligned}\iiint\limits_\Omega zdxdydz&=\iint\limits_{D_{xy}}dxdy\int^4_{x^2+y^2}zdz\&=\int^{2\pi}0d\theta\int^2_0rdr\int^4{r^2}zdz\&=\frac{64}3\pi\end{aligned}$

三、利用球坐标计算

适用于$\Omega$为球，或被积函数$f(x^2+y^2+z^2)$

设在第一卦限内的一条直线，该直线与$z$轴为夹角设为$\phi$，该直线向$xoy$平面投影与$x$轴的夹角设为$\theta$

令$\begin{cases}x=r\sin\phi\cos\theta\y=r\sin\phi\sin\theta\z=r\cos\phi\end{cases}$

$dv=dxdydz=d\theta d\phi(r^2\sin\phi)dr\quad\theta\in[0,\pi],\phi\in[0,\frac\pi2]$

例3：求半径为$a$的球面与半顶角为$\alpha$的内接锥面所围成的立体的体积，如下图所示

（图中的$2a$标错地方了，应该在$z$轴最上面的点处）

从原点做直线，显然只会从球面穿出

$x^2+y^2+(z-a)^2=a^2$