【高等數學】重積分

二重積分的概念與性質

一、二重積分的定義

設$f(x,y)$是有界閉區域$D$上的有界函數，将閉區域$D$任意分成$n$哥小閉區域$\Delta\sigma_1,\Delta\sigma_2,\cdots,\Delta\sigma_n$，其中$\Delta\sigma_i$表示第$i$個小閉區域，也表示它的面積，在每個$\Delta\sigma_i$上任取一點$(\xi_i,\eta_i)\Delta\sigma_i\quad(i=1,2,3,\cdots,n)$，并作和$\sum^{n}{i=1}f(\xi_i,\eta_i)\Delta\sigma_i$，如果當各小閉區域的直徑中的最大值$\lambda\to0$時，這個和的極限總存在，且與閉區域$D$的分發及點$(\xi_i,\eta_i)$的取法無關，那麼稱此極限為函數$f(x,y)$在閉區域$D$上的二重積分，記作$\begin{aligned}\iint\limits{D}f(x,y)d\sigma=\lim_{\lambda\to0}\sum^n_{i=1}f(\xi_i,\eta_i)\Delta\sigma_i\end{aligned}$，其中$f(x,y)d\sigma$叫做被積表達式，$x$與$y$叫做積分變量，$D$叫做積分區域，$\sum^n_{i=1}f(\xi_i,\eta_i)\Delta\sigma_i$叫做積分和

二、二重積分的性質

性質1（線性）：設$\alpha$與$\beta$為常數，則$\iint\limits_D[\alpha f(x,y)+\beta g(x,y)]d\sigma=\alpha\iint\limits_Df(x,y)d\sigma+\beta\iint\limits_Dg(x,y)d\sigma$

性質2（區域可加）：如果閉區域$D$被有線條曲線分成有限個部分閉區域，那麼在$D$上的二重積分等于在各部分閉區域上的二重積分的和

例：如果$D$分成兩個閉區域$D_1$與$D_2$，則$\iint\limits_Df(x,y)d\sigma=\iint\limits_{D_1}f(x,y)d\sigma+\iint\limits_{D_2}f(x,y)d\sigma$

性質3：如果在$D$上，$f(x,y)=1$，$\sigma$是$D$的面積，那麼$\sigma=\iint\limits_D1d\sigma=\iint\limits_Dd\sigma$

性質4：如果在$D$上，$f(x,y)\leq g(x,y)$，那麼有$\iint\limits_Df(x,y)d\sigma\leq\iint\limits_Dg(x,y)d\sigma$。特殊地，由于$-|f(x,y)|\leq f(x,y)\leq|f(x,y)|$，是以$|\iint\limits_Df(x,y)d\sigma|\leq\iint\limits_D|f(x,y)|d\sigma$

性質5：設$M$和$m$分别是$f(x,y)$在閉區域$D$上的最大值和最小值，$\sigma$是$D$的面積，則有$m\sigma\leq\iint\limits_Df(x,y)d\sigma\leq M\sigma$

證明：

設$m\leq f(x,y)\leq M$

由性質4知，$\iint\limits_Dmd\sigma\leq\iint\limits_Df(x,y)d\sigma\leq\iint\limits_DMd\sigma$，即$m\iint\limits_Dd\sigma\leq\iint\limits_Df(x,y)d\sigma\leq M\iint\limits_Dd\sigma$

由性質3得，$m\sigma\leq\iint\limits_Df(x,y)d\sigma\leq M\sigma$

證畢

性質6（二重積分的中值定理）：設函數$f(x,y)$在閉區域$D$上連續，$\sigma$是$D$的面積，則在$D$上至少存在一點$(\xi_i,\eta_i)$，使得$\iint\limits_Df(x,y)d\sigma=f(\xi,\eta)\cdot\sigma$

證明：

$\sigma\ne0$

由性質5知，兩邊同除$\sigma$得，$m\leq\frac1\sigma\iint\limits_Df(x.y)d\sigma\leq M$

又$\because f(x,y)$在區域$D$上連續

由閉區域連續函數的介值定理可知，在區域$D$上至少存在一點$(\xi,\eta)$

使$f(\xi,\eta)=\frac1\sigma\iint\limits_Df(x,y)d\sigma$

即$\iint\limits_Df(x,y)d\sigma=f(\xi,\eta)\cdot\sigma$

二重積分的計算法

一、利用直角坐标計算二重積分

1. $X$型區域

區域$D$由$\begin{cases}y_1(x)\leq y\leq y_2(x)\a\leq x\leq b\end{cases}$确定

1. 先确定$x$的範圍
2. 再任取$x$，沿$y$軸的正方向穿針，穿入為下限，穿出為上限

$\iint\limits_Df(x,y)d\sigma=\int^b_adx\int^{y_2(x)}_{y_1(x)}f(x,y)dy$

2. $Y$型區域

區域$D$由$\begin{cases}x_1(y)\leq x\leq x_2(y)\c\leq y\leq d\end{cases}$确定

1. 先确定$y$的範圍
2. 再任取$y$，沿$x$軸的正方向穿針，穿入為下限，穿出為上限

$\iint\limits_Df(x,y)d\sigma=\int^d_cdy\int^{x_2(y)}_{x_1(y)}f(x,y)dx$

例1：計算$\iint\limits_Dxyd\sigma$，其中$D$是由抛物線$y^2=x$及直線$y=x-2$所圍成的閉區域

ax = plt.gca()

ax.spines['right'].set_color('none')

ax.spines['top'].set_color('none')

ax.spines['bottom'].set_position(('data', 0))

ax.spines['left'].set_position(('data',0))

ax.set_aspect(1)

plt.rcParams['figure.figsize']=(8,6)

X=np.arange(-5,5,0.002)

f1=lambda x:x-2

f2=lambda x:x**0.5

f3=lambda x:-x**0.5

s1=pd.Series(f1(X),index=X)

s2=pd.Series(f2(X),index=X)

s3=pd.Series(f3(X),index=X)

s1.plot()

s2.plot(color='orange')

s3.plot(color='orange')

plt.ylim(-2,3)

plt.xlim(-1,5)

           

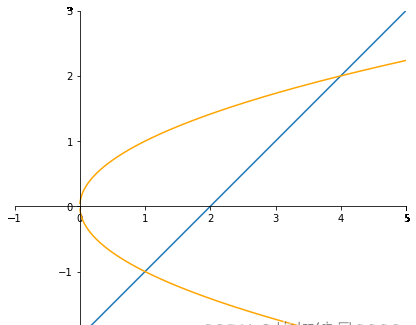
聯立$\begin{cases}y^2=x\y=x-2\end{cases}$解得$\begin{cases}x=1\y=-1\end{cases}\quad\begin{cases}x=4\y=2\end{cases}$

先$y$後$x$

原式$\begin{aligned}=\int^1_0dx\int^{\sqrt x}{-\sqrt x}xydy+\int^4_1dx\int^{\sqrt x}{x-2}xydy=\frac{45}8\end{aligned}$

先$x$後$y$

$\begin{aligned}\text{原式}&=\int^2_{-1}dy\int^{y+2}{y^2}xydx\&=\int^2{-1}(\frac12yx^2)\Big|^{y+2}{y^2}dy\&=\frac12\int^2{-1}(y^3+4y^2+4y-y^5)dy\&=\frac{45}8\end{aligned}$

二、利用極坐标計算二重積分

适用情況：一般适用于圓域、部分圓域，被積函數有$(x^2+y^2)$的函數

極坐标的做法：

$\begin{cases}x=r\cdot\cos\theta\y=r\cdot\sin\theta\end{cases}\quad\begin{cases}\alpha\leq\theta\leq\beta\r_1(\theta)\leq r\leq r_2(\theta)\end{cases}$

$\begin{aligned}\iint\limits_Df(x,y)d\sigma=\int^\beta_\alpha\theta\int^{r_2(\theta)}_{r_1(\theta)}f(r\cos\theta,r\sin\theta)rdr\end{aligned}$

其中$d\sigma=dxdy=r\cdot d\theta dr$

若積分區域$D$包含原點，則$r$的下限一定為$0$

例2：計算$\iint\limits_D\arctan\frac yxd\sigma$其中$D$是由圓周$x^2+y^2=4,x^2+y^2=1$及直線$y=0,y=x$所圍成的在第一象限的閉區域

ax=plt.gca()

ax.spines['right'].set_color('none')

ax.spines['top'].set_color('none')

ax.spines['bottom'].set_position(('data', 0))

ax.spines['left'].set_position(('data',0))

ax.set_aspect(1)

plt.rcParams['figure.figsize']=(8,6)

X1=np.linspace(0,2,50)

# np.arange會出現x取不到端點值，改用np.linspace

print(X1)

f1=lambda x:(4-x**2)**0.5

X2=np.linspace(0,1,50)

f2=lambda x:(1-x**2)**0.5

s1=pd.Series(f1(X1),index=X1)

s2=pd.Series(f2(X2),index=X2)

s1.plot()

s2.plot(color='orange')

           

$\begin{aligned}\text{原式}&=\int^{\frac\pi4}_0d\theta\int^2_1\arctan\frac{r\sin\theta}{r\cos\theta}rdr\&=\int^{\frac\pi4}_0d\theta\int^2_1\arctan(\tan\theta)rdr\&=\int^{\frac\pi4}_0\theta d\theta\int^2_1rdr\&=(\frac12\theta^2)\Big|^\frac\pi4_0(\frac12r^2)\Big|^2_1\&=\frac3{64}\pi^2\end{aligned}$

三重積分

一、三重積分的概念

定義：設$f(x,y,z)$是空間有界閉區域$\Omega$上的有界函數。将$\Omega$任意分成$n$個小閉區域$\Delta v_1,\Delta v_2,\cdots,\Delta v_n$，其中$\Delta v_i$表示第$i$個小閉區域，也表示它的體積。在每個$\Delta v_i$上任取一點$(\xi_i,\eta_i,\zeta_i)$，作乘積$f(\xi_i,\eta_i,\zeta_i)\Delta v_i\quad(i=1,2,\cdots,n)$，并作和$\sum^n_{i=1}f(\xi_i,\eta_i,\zeta_i)\Delta v_i$。如果當各小閉區域直徑中的最大值$\lambda\to0$時，這個和的極限總存在，且與閉區域$\Omega$的分法及點$(\xi_i,\eta_i,\zeta_i)$的取法無關，那麼稱此極限為函數$f(x,y,z)$在閉區域$\Omega$上的三重積分，記作$\iiint\limits_\Omega f(x,y,z)dv$，即$\iiint\limits_\Omega f(x,y,z)dv=\lim_{\lambda\to0}\sum^n_{i=1}f(\xi_i,\eta_i,\zeta_i)\Delta v_i$，其中$f(x,y,z)$叫做被積函數，$dv$叫做體積函數，$\Omega$叫做積分區域

二、三重積分的計算

1. 利用直角坐标計算

先一後二（投影法）

方法

1. 先投影，确定$(x,y)$範圍
2. 再任取$(x,y)$，沿$z$軸正方向穿針，确定$z$的範圍，傳入為下限，穿出為上限。則$\iiint\limits_\Omega f(x,y,z)dv=\iint\limits_{D_{xy}}dxdy\int^{z_2(x,y)}_{z_1(x,y)}f(x,y,z)dz$

先二後一（截面法）

方法

1. 先确定$z$的範圍
2. 再任取$z$做截面，确定$(x,y)$的範圍。則$\iiint\limits_\Omega f(x,y,z)dv=\int^b_adz\iint\limits_{D_{xy}}f(x,y,z)dxdy$

例1：計算三重積分$\iiint\limits_\Omega xdxdydz$，其中$\Omega$為三個坐标面及平面$x+2y+z=1$所圍成的閉區域

先一後二

$\begin{aligned}\iiint\limits_\Omega xdxdydz&=\iint\limits_{D_{xy}}xdxdy\int^{1-x-2y}0dz\&=\iint\limits{D_{xy}}x(1-x-2y)dxdy\&=\int^1_0dx\int^{\frac12-\frac x2}_0(x-x^2-2xy)dy\&=\frac14\int^1_0(x-2x^2+x^3)dx\&=\frac1{48}\end{aligned}$

先二後一

$\begin{aligned}\iiint\limits_\Omega xdxdydz&=\int^1_0dz\iint\limits_{D_z}xdxdy\&=\int^1_0dz\int^{1-z}_0dx\int^{\frac12(1-x-z)}_0xdy\&=\frac1{48}\end{aligned}$

取高度為$z$的投影（此時$z$為常數），用截面确定$(x,y)$範圍。

将該截面向$xoy$平面做投影，易得x的範圍為$[1,z]$，由于$z$為常數，是以此時的斜線方程即為$x+2y+z=1$，可得$y$的範圍為$[0,\frac12(1-x-z)]$

二、利用柱坐标計算

無論是利用柱坐标還是球坐标，由于已經将$x,y,z$替換掉了，是以整個式子中不能再出現$x,y,z$，包括積分上下限

适用于$\Omega$為圓柱（$x^2+y^2=a^2$），圓錐（$z=a\sqrt{x^2+y^2}$），旋轉抛物面（$z=a(x^2+y^2)$），被積函數有$(x^2+y^2)$

令$\begin{cases}x=r\cos\theta\y=r\sin\theta\z=z\end{cases}$，則$dv=d\theta rdrdz$

例2：利用柱坐标計算三重積分$\iiint\limits_\Omega zdxdydz$，其中$\Omega$是由曲面$z=x^2+y^2$與平面$z=4$所圍成的閉區域

$\begin{aligned}\iiint\limits_\Omega zdxdydz&=\iint\limits_{D_{xy}}dxdy\int^4_{x^2+y^2}zdz\&=\int^{2\pi}0d\theta\int^2_0rdr\int^4{r^2}zdz\&=\frac{64}3\pi\end{aligned}$

三、利用球坐标計算

适用于$\Omega$為球，或被積函數$f(x^2+y^2+z^2)$

設在第一卦限内的一條直線，該直線與$z$軸為夾角設為$\phi$，該直線向$xoy$平面投影與$x$軸的夾角設為$\theta$

令$\begin{cases}x=r\sin\phi\cos\theta\y=r\sin\phi\sin\theta\z=r\cos\phi\end{cases}$

$dv=dxdydz=d\theta d\phi(r^2\sin\phi)dr\quad\theta\in[0,\pi],\phi\in[0,\frac\pi2]$

例3：求半徑為$a$的球面與半頂角為$\alpha$的内接錐面所圍成的立體的體積，如下圖所示

（圖中的$2a$标錯地方了，應該在$z$軸最上面的點處）

從原點做直線，顯然隻會從球面穿出

$x^2+y^2+(z-a)^2=a^2$